Comprendre les Fractions équivalentes

Les fractions équivalentes représentent la même partie d’un tout

La meilleure façon de penser aux fractions équivalentes est qu’il s’agit de fractions ayant la même valeur globale.

Par exemple, si nous coupons une tarte exactement au milieu, en deux morceaux de taille égale, une pièce équivaut à la moitié de la tarte.

Et si une autre tarte (de même taille) est coupée en 4 morceaux égaux, alors deux morceaux de cette tarte représentent la même quantité de tarte que 1/2.

On peut donc dire que 1/2 est équivalent (ou égal) à 2/4.

Ne laissez pas les fractions équivalentes vous confondre!

Regardez les quatre cercles ci-dessus.Pouvez-vous voir que celui « 1/2″, les deux ”1/4″ et les quatre ”1/8 » occupent la même quantité de surface colorée en orange pour leur cercle?Eh bien, cela signifie que chaque zone colorée en orange est une fraction équivalente ou une quantité égale. Par conséquent, nous pouvons dire que 1/2 est égal à 2/4, et 1/2 est également égal à 4/8. Et oui sauterelle, 2/4 est une fraction équivalente pour 4/8 too.As vous le savez déjà, nous sommes fous de règles. Regardons donc la règle pour vérifier si deux fractions sont équivalentes ou égales. La règle pour les fractions équivalentes peut être un peu difficile à expliquer, mais accrochez-vous, nous éclaircirons les choses en un peu plus.

Voici la règle

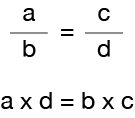
Cette règle dit que deux fractions ne sont équivalentes (égales) que si le produit du numérateur (a) de la première fraction et du dénominateur (d) de l’autre fraction est égal au produit du dénominateur (b) de la première fraction et du numérateur (c) de l’autre fraction.

Un produit signifie simplement que vous multipliez.

Cela ressemble à une bouchée, alors essayons-le avec des nombres

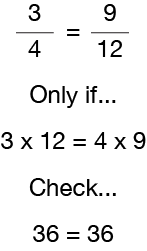
Testez la règle

Maintenant, branchez les nombres dans la Règle pour les fractions équivalentes pour être sûr que vous l’avez « froid”. 3/4 n’est équivalent (égal) à 9/12 que si le produit du numérateur (3) de la première fraction et du dénominateur (12) de l’autre fraction est égal au produit du dénominateur (4) de la première fraction et du numérateur (9) de l’autre fraction. Nous savons donc que 3/4 équivaut à 9/12, car 3×12 = 36 et 4×9 = 36. Un moyen simple de vérifier les fractions équivalentes est de faire ce qu’on appelle la « multiplication croisée”, ce qui signifie multiplier le numérateur d’une fraction par le dénominateur de l’autre fraction. Ensuite, faites la même chose en sens inverse. Comparez maintenant les deux réponses pour voir si elles sont égales. Si elles sont égales, alors les deux fractions sont des fractions équivalentes.

Le graphique ci-dessous vous montre comment croiser la multiplication…

D’accord, faisons-en un avec des nombres où les fractions ne sont pas équivalentes

Comme vous pouvez le voir dans cet exemple, 1/2 n’est pas une fraction équivalente de 2/3.

Si vous n’oubliez pas d’utiliser la méthode de multiplication croisée, vous ne devriez pas avoir de problèmes pour vérifier les fractions équivalentes.

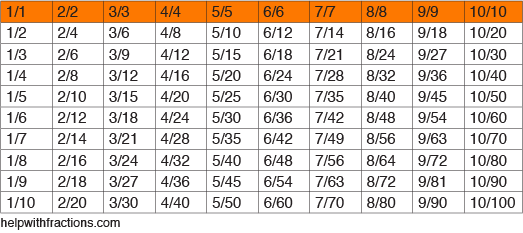
Le tableau ci-dessous répertorie quelques fractions communes et leurs équivalents. Il suffit de lire le tableau de gauche à droite. Ce qu’il montre, ce sont des valeurs multipliées par différentes variations de fractions égales à « 1”. Vous vous souvenez que tout nombre divisé par lui-même est égal à « 1”, n’est-ce pas?