Aux portes de Paris, à huit mètres sous terre dans une voûte climatisée, se trouve un cylindre en alliage de platine vieux de 143 ans. Mesurant seulement 39 mm de haut, il n’a jamais été touché par des mains humaines. Tel une délicate poupée russe, le cylindre est mis en cage à l’intérieur de trois cloches de verre imbriquées dans une pièce accessible uniquement avec trois clés conservées par trois personnes différentes. Autour de l’objet mystérieux se trouvent « les témoins”: six cylindres « identiques” coulés dans le même alliage de platine.

Bien que les efforts de préservation rivalisent avec ceux du Suaire de Turin, le cylindre n’est pas un objet religieux sacré. C’est le Kilogramme Prototype International (IPK), le seul et unique kilogramme vrai par rapport auquel tous les autres sont mesurés. Installé dans le Pavillon de Breteuil – siège du Bureau International des Poids et mesures (BIPM) – l’IPK va bientôt perdre son statut unique et devenir une relique d’une époque révolue. Il sera alors aussi pittoresque que le Mètre Prototype International (IPM) – une barre en alliage de platine également logée au BIPM – qui a servi de mètre officiel au monde jusqu’en 1960.

Le 16 novembre 2018, des métrologues et des décideurs politiques de 60 pays à travers le monde se réuniront à la Conférence Générale des Poids et Mesures (CGPM) à Versailles, en France. Rien d’inhabituel là-bas, car la réunion se réunit une fois tous les quatre ans pour discuter des budgets et des questions de métrologie. Mais cette réunion sera spéciale. Les États membres voteront sur l’adoption ou non du changement le plus radical apporté au Système International d’Unités (Système International, ou SI) depuis sa création en 1960. C’est un changement qui comprendra de nouvelles définitions du kelvin, de l’ampère et de la taupe, mais peut-être le plus important du kilogramme.

Chaque État membre votera lors d’un processus qui sera diffusé en direct en ligne. Si le changement est ratifié (et tous les signes sont qu’il le sera), l’événement marquera la fin de la base des unités sur des objets – une pratique datant de millénaires. Il répondra également enfin à un souhait exprimé pour la première fois par James Clerk Maxwell, qui avait prédit que les étalons de mesure pourraient en quelque sorte être définis par des constantes immuables de la nature.

Une base solide

S’exprimant lors d’une réunion de l’Association britannique pour l’avancement de la Science à Liverpool en 1870, Maxwell a déclaré aux délégués que « Si wishnous voulons obtenir des étalons de longueur, de temps et de masse qui seront absolument permanents, nous devons les rechercher non pas dans les dimensions, ou le mouvement, ou la masse de notre planète, mais dans la longueur d’onde, la période de vibration et la masse absolue de ces molécules impérissables, inaltérables et parfaitement similaires. »

Les initiés ne voyant aucun indice de résultat négatif lors de la réunion du BIPM ce mois-ci, il est prudent de supposer que la résolution visant à réformer l’IS passera sans opposition et que le désir de Maxwell de normes ”absolument permanentes » sera réalisé. Le nouvel IS entrera alors officiellement en vigueur le 20 mai 2019, précisément une douzaine de dizaines (144) ans après le premier traité international sur les unités de mesure – la Convention du mètre – qui a été signé le même jour en 1875. Mais pourquoi est-il si important que les unités soient basées sur des constantes de la nature?

Les unités sont un aliment de base de la société depuis au moins l’époque des anciens Égyptiens. Ils ont utilisé différentes parties du corps humain ou des objets de leur environnement comme échelles pour mesurer les choses. Pourtant, ces normes pourraient être très différentes d’un endroit à l’autre. Pour les philosophes de la nature en Europe des XVIIe et XVIIIe siècles, la variabilité unitaire – en particulier en longueur et en masse – rendait presque impossible la comparaison des résultats pour le même phénomène physique s’il avait été mesuré à différents endroits.

Diverses tentatives ont été faites pour créer une mesure universelle et, en 1799, la France a introduit le système métrique, basé sur deux unités – le mètre et le kilogramme. Connus sous le nom de Mètre des Archives et de Kilogramme des Archives, ces deux objets en platine ont été stockés aux Archives Nationales à Paris pour définir juridiquement et pratiquement les unités. Ces normes ont duré 90 ans jusqu’à ce qu’elles soient remplacées par l’IPM et l’IPK, qui étaient physiquement plus difficiles et mieux conçues.

Pensée universelle

Les unités SI sont devenues entrelacées dans la science. Du joule définissant l’énergie au katal pour mesurer l’activité catalytique, les 29 unités SI nommées peuvent être définies par une combinaison de seulement sept unités de base: la seconde, le mètre, le kilogramme, l’ampère, le kelvin, la mole et le candela. Mais alors que la science devenait de plus en plus précise au 20e siècle, un nouveau problème s’est posé. Toute unité basée sur quelque chose – un objet, une expérience ou un phénomène – qui n’est pas universelle sera instable.

Considérez la seconde. Elle est historiquement liée à la révolution de la Terre, qui est définie comme prenant 24 heures, où une heure est de 60 minutes et une minute de 60 secondes. Mais que se passe-t-il si la Terre commence à tourner plus lentement, comme elle le fait même si légèrement? Une journée sera plus longue, ce qui signifie qu’une seconde sera également plus longue en termes réels. Cela signifie qu’une voiture enregistrant 30 km / h roulera en fait un peu plus lentement, une ampoule de 30 W sera un peu plus faible et, plus absurde encore, l’univers se développera à un rythme différent.

Si, cependant, la notion et la durée d’une seconde sont conservées mais que la rotation de la Terre est supprimée de la définition et remplacée par quelque chose qui ne change jamais où et quand elle est mesurée dans l’univers, la seconde devient stable. Cela a été fait en 1967, lorsque le second a été redéfini comme 9 192 631 770 fois la période du rayonnement correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133, Δν (voir « Une brève histoire de la conservation du temps” par Helen Margolis).

Plus tard, en 1983, le mètre a également été redéfini, comme la longueur du trajet parcouru par la lumière dans le vide pendant un intervalle de temps de 1/299 792 458 secondes. La précision exquise avec laquelle les scientifiques ont pu mesurer le temps et la distance a profité à la société, notamment en conduisant à des systèmes de positionnement par satellite, notamment le GPS.

Planck à la rescousse

Bien qu’ayant bien servi la société pendant 143 ans, définir le kilogramme en termes d’objet unique est une notion intrinsèquement instable. En effet, si l’IPK devient plus léger ou plus lourd, même d’une infime quantité, la masse de l’univers exprimée en kilogrammes change également – une proposition folle. De manière plutôt inquiétante, l’IPK a changé. Lorsque les métrologues l’ont mesurée en 1988-1991, l’IPK avait une masse d’environ 50 µg de moins en moyenne que les six témoins. Par définition, cela signifie que les témoins avaient gagné une infime quantité de masse d’une manière ou d’une autre, peut-être en absorbant des molécules d’air. Mais le plus probable – étant donné que de nombreuses copies nationales du kilogramme semblaient également gagner de la masse – est que l’IPK avait perdu de la masse. Ou peut-être qu’ils avaient tous gagné ou perdu de la masse, juste à des rythmes différents.

Les métrologues n’ont constaté aucune autre dérive entre l’IPK et les témoins de 1991 à 2014, la dernière fois que des mesures ont été effectuées. Mais le fait qu’il n’y ait pas eu de dérive ne signifiait pas que la masse de l’IPK ou des témoins n’avait pas changé. Ils ont peut-être simplement perdu ou gagné de la masse en tandem. Et c’est le problème: il n’y a aucun moyen de le dire car la masse est toujours calibrée par rapport à l’IPK.

 » Avec l’IS révisé, nous n’aurons pas à nous soucier de ce genre de choses ”, explique Richard Davis, ancien chef de la division masse du BIPM qui est maintenant consultant auprès du bureau. Au lieu d’être défini par la masse d’un cylindre de métal, dans le nouveau SI, le kilogramme sera basé sur une constante fondamentale de la physique quantique: la constante de Planck.

Du nom de Max Planck, qui a développé l’idée que l’énergie provient de petits paquets appelés quanta, la constante de Planck, h, relie l’énergie d’un quantum de rayonnement électromagnétique à sa fréquence par la célèbre formule E = hv. La constante de Planck est à son tour liée à la masse via E= mc2 d’Einstein. Actuellement, h a une valeur mesurée d’environ 6,62607 × 10-34 m2 kg s-1, mais les métrologues veulent maintenant fixer sa valeur dans la pierre, le kilogramme étant défini en fonction de cette valeur.

Ce sera donc adieu à l’IPK, qui est un objet physiquement instable, et adieu à l’incertitude dans la valeur de la constante de Planck. « Après la redéfinition, la constante de Planck inébranlable est fixée à une valeur, tandis que l’incertitude est plus appropriée à la masse de l’IPK”, explique Stephan Schlamminger, métrologue du National Institute of Standards and Technology, aux États-Unis. « Et avec une constante de planche fixe, de meilleurs appareils pourront réaliser un kilogramme de plus en plus précisément. »

Watt voulez-vous dire

Pour commencer du bon pied, il est important que la valeur à laquelle la constante de Planck est fixée soit mesurée aussi précisément que possible actuellement. Cette responsabilité repose sur les mesures de deux types d’expériences très différents. Le premier d’entre eux s’appelle une balance à croquettes, anciennement appelée balance à watts mais maintenant renommée en l’honneur de son inventeur Bryan Kibble du Laboratoire national de physique du Royaume-Uni, décédé en 2016. Actuellement, seuls la France, le Canada et les États-Unis disposent de balances croquettes capables d’effectuer les mesures nécessaires pour fixer la constante de Planck. Cependant, beaucoup d’autres travaillent à la construction de leurs propres équilibres. Comme un ensemble de balances de haute technologie, la balance à croquettes utilise les forces électromagnétiques fournies par une bobine de fil immergée dans un champ magnétique pour équilibrer une masse de kilogramme. L’équipement permet aux métrologues de prendre des valeurs précises de courant et de tension, à partir desquelles la constante de Planck peut être dérivée (voir encadré ci-dessous).

La balance des croquettes

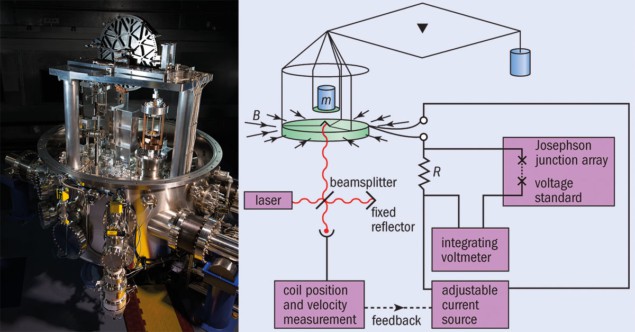
C’est quoi ? La balance à croquettes (ou watt) consiste en une bobine circulaire horizontale de fil de longueur, L, suspendue à un bras d’une balance. La bobine est placée dans un fort champ magnétique, B, et un courant électrique, I, la traverse générant une force, F = BIL, qui peut être ajustée pour être égale au poids d’une masse placée sur le même bras de la balance (mg). La masse est alors donnée par m = BIL/g.

Quel est le problème ? Bien que je puisse être mesuré avec précision, il est difficile de faire de même pour B et L.

Alors quelle est la solution? Les métrologues retirent la masse et déplacent la bobine à la vitesse u dans le champ magnétique pour générer une tension V = BLu. Le dispositif est appelé balance du watt car, en réarrangeant les deux équations, la puissance électrique (VI) est équilibrée par la puissance mécanique (mgu). En d’autres termes, m = VI/gu. Comme u est facile à mesurer et que g (l’accélération due à la gravité) est bien connue, les problèmes de mesure de B et L ont disparu.

Mais quel est le lien avec la constante de Planck, h ? C’est le plus malin. Le courant est déterminé en le faisant passer à travers une résistance et en utilisant l’effet Josephson pour mesurer la chute de tension qui en résulte. Cet effet décrit le fait que si deux supraconducteurs sont séparés par un isolant mince, des paires d’électrons dans chaque couche se couplent de sorte que le rayonnement hyperfréquence de fréquence, f, crée une tension aux bornes de la couche de V = hf/2e, où e est la charge sur l’électron. La résistance de la résistance peut être mesurée car le flux d’électrons dans les systèmes 2D à des températures ultra-basses est quantifié, la conductivité augmentant en multiples de e2 / h.

Alors pourquoi est-ce bon pour la métrologie? Jusqu’à présent, une balance à croquettes mesurait h en unités SI. Mais lorsque la définition du kilogramme est modifiée, la valeur numérique de h sera fixée dans la pierre, permettant à quiconque d’utiliser la balance pour mesurer la masse avec une précision exquise.

La deuxième façon de mesurer h est appelée densité cristalline aux rayons X (XRCD) ou expérience d’Avogadro. Il s’agit d’un cristal uniforme de silicium – 28 atomes qui a été usiné en une sphère presque parfaitement ronde de 1 kg. En utilisant l’interférométrie optique, les métrologues calculent d’abord le diamètre global – et donc le volume – de la sphère. Ensuite, en combinant l’interférométrie optique avec l’analyse aux rayons X, ils peuvent calculer l’espacement entre les atomes, le volume occupé par chacun, et donc le nombre total d’atomes dans la sphère. Enfin, en pesant la sphère, ils peuvent déterminer la constante d’Avogadro. Cette approche définit combien d’atomes ou de molécules il y a dans une mole d’une substance – une quantité tout à fait différente de la masse, qui définira maintenant la mole elle-même. Une équation de la physique atomique qui relie les constantes d’Avogadro et de Planck permet alors de capturer une valeur précise de cette dernière.

Les laboratoires du monde entier ont utilisé ces deux techniques différentes pour mesurer la constante de Planck avec une précision extraordinaire pour donner une valeur finale convenue de 6,626 070 150 × 10-34 kg m2 s–1, avec une incertitude relative de seulement 10 parties par milliard (2018 Metrologia 55 L13). Quant à la constante d’Avogadro, elle sera fixée à 6,022,140, 76 × 1023 mol–1. Et une fois les constantes de Planck et d’Avogadro fixées, les expériences complexes dont elles ont été dérivées peuvent être utilisées comme étalons pour mesurer un kilogramme et une mole.

Impact pratique

Le moyen le plus simple d’expliquer comment cela fonctionnera est de considérer l’équilibre des croquettes. Jusqu’à présent, il a été utilisé pour mesurer des valeurs précises de courant et de tension qui sont ensuite branchées dans des équations pour obtenir la constante de Planck. À l’avenir, la constante de Planck sera une valeur fixe et ces mêmes mesures donneront plutôt la masse sur le balancier. En d’autres termes, toute personne ayant accès à une balance de croquettes peut réaliser un kilogramme parfait. Le même principe s’appliquera également à l’ampère et au kelvin, qui seront à l’avenir donnés en termes de charge sur un électron, e, et de constante de Boltzmann, k, respectivement. Les équipements conçus pour mesurer précisément ces constantes fondamentales vont maintenant être tournés sur leur tête pour réaliser avec précision les unités d’ampère et de kelvin (voir encadré ci-dessous). Quant au mètre, à la seconde et à la candela, leurs définitions seront modifiées mais resteront effectivement inchangées.

En dehors de la métrologie, le nouveau SI aura peu de conséquences pratiques immédiates et passera inaperçu de la plupart des gens. Après tout, les unités peuvent être définies différemment, mais l’objectif est toujours de garder la même taille. Pourtant, définir le kilogramme, le kelvin, l’ampère et la taupe de manière entièrement nouvelle basée sur des constantes de la nature les rend invariants, accessibles et pratiques. Par conséquent, les scientifiques pourront les mesurer à n’importe quel endroit ou heure, et à n’importe quelle échelle.

« Pour la première fois, nous pourrons mesurer des quantités minuscules et énormes avec la même très grande précision car les constantes fondamentales ne se soucient pas d’une échelle”, ajoute Schlamminger. C’est important. Avant la redéfinition du mètre, la longueur ne pouvait être mesurée que très précisément autour d’un mètre. Mais depuis sa redéfinition, les applications de haute précision comme la microélectronique ont énormément bénéficié de la précision avec laquelle elles peuvent mesurer la distance à de minuscules échelles.

De même, le nouveau kilogramme permettra de mesurer un kilogramme, un gramme et un milligramme avec une précision identique, même au point que les masses atomiques seront mesurées en kilogrammes. Tant qu’il existe une connexion expérimentale à la constante de Planck, la masse pourra être mesurée. Par conséquent, les métrologues sont en course pour construire des balances de croquettes de table et de nouveaux appareils qui mesurent la masse exactement à des échelles grandes et petites. Ainsi, la nouvelle unité de masse et les unités SI sont généralement enfin adaptées au 21e siècle et le resteront si longtemps dans le futur. Comme Schlamminger le conclut avec justesse: « Le nouveau SI est une construction de beauté et de logique.”

• Pour en savoir plus sur les nouvelles définitions de SI, consultez l’ebook gratuit de Physics World Discovery Redéfinissant le kilogramme et d’autres unités de SI de Stephan Schlamminger à www.physicsworlddiscovery.org