La conservation de l’élan est un concept fondamental de la physique parallèlement à la conservation de l’énergie et à la conservation de la masse.La quantité de mouvement est définie comme étant la masse d’un objet multipliée par la vélocité de l’objet.La conservation de l’élan indique que, dans un domaine problématique, la quantité d’élan reste constante;l’élan n’est ni créé ni détruit, mais seulement changéà travers l’action des forces telles que décrites par les lois du mouvement de Newton.Il est plus difficile de gérer l’élan que la masse et l’énergie, car le momentum est une quantité avectrice ayant à la fois une magnitude et une direction. L’élan est conservé dans les troisdirections physiques en même temps. C’est encore plus difficile lorsqu’il s’agit d’agasparce que les forces dans une direction peuvent affecter l’élan dans une autre directionà cause des collisions de nombreuses molécules.Sur cette diapositive, nous présenterons un problème d’écoulement très, très simplifié où les propriétés ne changent que dans une direction.Le problème est encore simplifié en considérant un écoulement régulier qui ne change pas avec le temps et en limitant les forces aux seules forces associées à thepressure.Be conscient que les problèmes de flux réels sont beaucoup plus complexes que ce simple exemple.

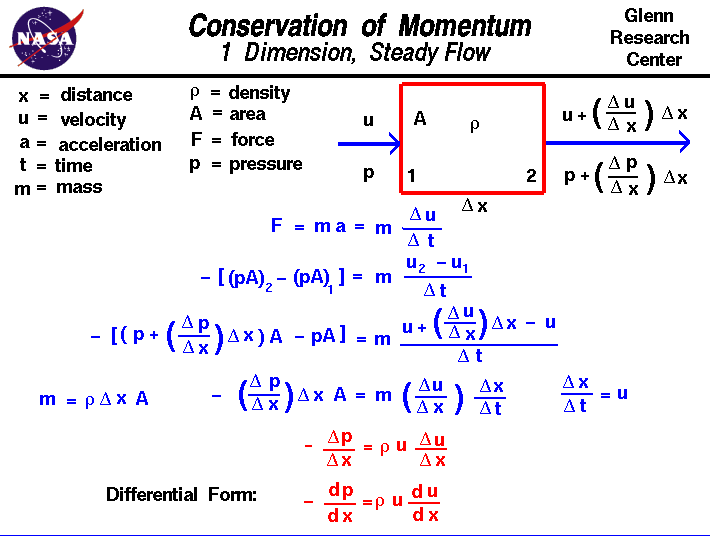
Considérons l’écoulement d’un gaz à travers un domaine dans lequel les propriétés d’écoulementseulement changer dans une direction, que nous appellerons « x ». Le gaz entre dans le domaine de la station 1 avec une certaine vitesse u et une certaine pression p et sort à la station 2 avec une valeur différente de vitesse et de pression. Pour simplifier, nous supposerons que la densité r reste constante dans le domaine et que la zone A à travers laquelle le gaz circule reste également constante. L’emplacement des stations 1 et 2 est séparépar une distance appelée del x. (Delta est le petit triangle sur la glisseet est la lettre grecque « d ». Les mathématiciens utilisent souvent ce symbole pour dénoterun changement ou une variation d’une quantité. La police d’impression Web ne supporte pasles lettres grecques, nous allons donc simplement l’appeler « del ».) Un changement de distance est appelé gradient pour éviter toute confusion avec un changement de temps appelé taux.Le gradient de vitesse est indiqué par del u / del x; le changement de vitesse par changement de distance. Ainsi, à la station 2, la vitesse est donnée par la vitesse à 1 plus le gradient multiplié par la distance.

Une expression similaire donne la pression à la sortie:

La seconde loi des états de mouvement de Newton dont la force F est égale au changement d’élan avec le respect du temps. Pour un objet de masse constante, cela réduit à l’accélération des temps de masse a.An l’accélération est un changement de vitesse avec un changement de temps (del u / del t). Ensuite :

La force dans ce problèmesvient du gradient de pression. Puisque la pression est une force par unité de surface, la force nette sur notre domaine de fluide est le temps de pression de la zone au sortir moins le temps de pression de la zone à l’entrée.

Le signe moins au début de cette expression est utilisé car les gaz passent d’une région de haute pression à une région de basse pression; si la pression augmente avecx, la vitesse diminuera. En remplaçant nos expressions pour la vitesse et la pression :

Simplifier:

Notant que (del x/del t) est la vitesse et que la masse est la densité r fois le volume (surface fois del x):

e ne sais pas si vous avez besoin d’une solution simple, mais je n’ai pas besoin d’une solution simple, mais je ne peux pas utiliser cette solution. r*u*(del u/del x)

Les del p/del x et del u/del x représentent les gradients de pression et de vitesse.Si nous réduisons notre domaine à des tailles différentielles, ces gradients deviennent des différentiels :

Il s’agit d’une forme unidimensionnelle et stable de Equation.It il est intéressant de noter que la perte de charge d’un fluide (le terme à gauche) est proportionnelle à la fois à la valeur de la vitesse et au gradient de la vitesse.Une solution de cette équation d’élan nous donne la forme de la pression dynamique qui apparaît dans l’équation de Bernoulli.

Activités:
Visites guidées

• Équations de dynamique des Fluides de base:

Navigation..

Page d’accueil du Guide du débutant