Par Jason McCormick
Professeur agrégé, Génie civil &Génie de l’environnement, Université du Michigan, Ann Arbor, États-Unis

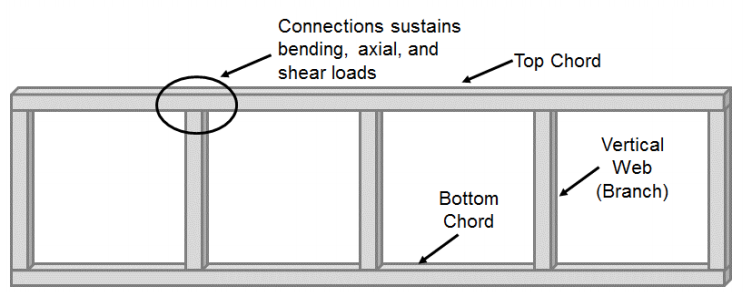
Les connexions instantanées constituées de sections structurelles creuses rectangulaires et carrées (HSS) ont reçu moins de considération que les connexions HSS à HSS constituées d’éléments chargés axialement (T, Y, croix et K – connexions). La majorité des études statiques portant sur ces connexions ont pris en compte les systèmes de fermes Vierendeel. Ces systèmes sont souvent formés par des cordes supérieures et inférieures carrées ou rectangulaires qui sont reliées à des éléments verticaux (branches) carrés ou rectangulaires (figure 1). En raison de cette configuration, la connexion corde à bande subit une flexion importante ainsi que des charges de cisaillement et axiales et n’est pas considérée comme une connexion épinglée comme cela se fait généralement dans les systèmes de fermes typiques. Conçu à l’origine en 1896 par Arthur Vierendeel, ce n’est que lorsque les SSH ont été développés que le potentiel des fermes Vierendeel a commencé à être réalisé (Korol et al. 1977), mais leur utilisation nécessitait une compréhension de la façon de transférer le moment entre les connexions T HSS à HSS.

Bon nombre des premières études de ces connexions se sont concentrées sur la capacité de la connexion à développer la pleine capacité de moment de l’élément de branche. Jubb et Redwood (1966) ont montré que lorsque la section de branche avait une largeur égale à la section de corde (β = 1), la pleine capacité de moment de l’élément HSS pouvait être atteinte sans renforcement. Cependant, cette étude n’a pas pris en compte la perte potentielle de capacité de moment due à la présence d’une charge axiale. D’autre part, Korol et coll. (1977) ont montré que les connexions avec une largeur de branche plus petite que la corde ne pouvaient pas développer la pleine capacité de moment de la branche sans renforcement grâce à une série de 29 tests de connexion différents prenant en compte 5 configurations différentes (plaques de renforcement de bride de branche non renforcées, raidisseurs de bride de corde, haubanage et pyramide tronquée). En général, la résistance et la rigidité des connexions de type Vierendeel non renforcées diminuent avec une augmentation du rapport d’élancement des cordes (B / t) et une diminution du rapport de largeur branche / corde (β). Par conséquent, les connexions de type treillis Vierendeel non déformées ne peuvent être considérées comme rigides (c.-à-d. subir une rotation relative minimale entre la corde et la branche) que lorsque le rapport de largeur branche-corde est de 1,0 et que le rapport d’élancement de la corde est faible ou que la connexion est renforcée (Packer, 1993).

Parce que les moments maximaux dans ces joints peuvent se produire à des déformations excessivement importantes, une approche similaire à celle utilisée pour les joints HSS carrés et rectangulaires à charge axiale est adoptée, où une capacité portante ultime ou une limite de déformation ou de rotation est utilisée pour caractériser le moment de conception (Wardenier 1982). L’AISC 360-10 (chapitre K3) considère trois états limites pour les connexions en T HSS carrées et rectangulaires sous flexion statique dans le plan: plastification de la paroi de corde, rendement local de la paroi latérale et rendement local de la branche en raison d’une répartition inégale de la charge. La plastification de la paroi de corde se produit du fait que la largeur de l’élément de dérivation est inférieure à la largeur de la corde (β ≤ 0,85), ce qui nécessite que les charges de tension et de compression produites par le moment de flexion soient transférées à travers la face relativement flexible de la corde plutôt que directement sur les parois latérales plus rigides. L’équation d’état limite (équation AISC 360-10 K3-6) peut être dérivée de la théorie des droites de rendement (Figure 2) :

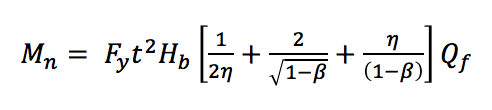
Mn est la capacité nominale de moment de la connexion, Fy est la limite d’élasticité minimale spécifiée de la corde, Hb est la hauteur totale de la branche, h est le paramètre de longueur de charge égal à la hauteur de la branche divisée par la largeur de la corde (en supposant un angle de 90o entre la corde et l’élément de branche comme c’est typique des fermes Vierendeel ), et Qf est un paramètre permettant de réduire la capacité de l’articulation en présence d’une compression axiale dans la corde.

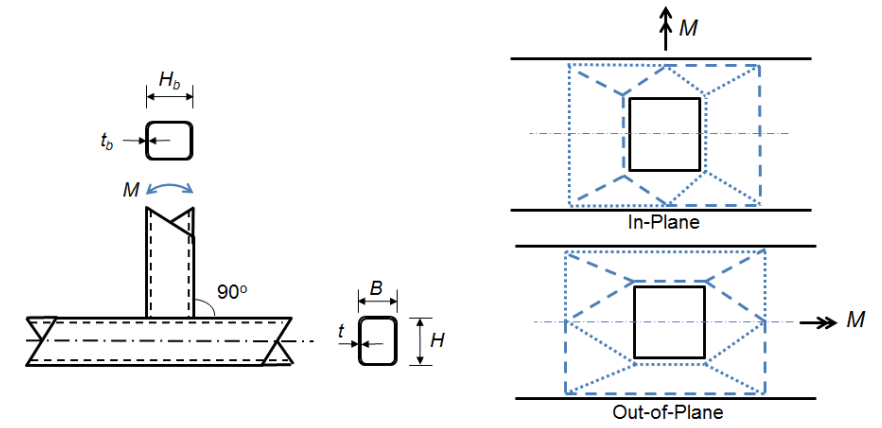
Les deux autres états limites sont associés à des connexions où la largeur de l’élément de branche est égale ou presque égale à la largeur de la corde (β >0.85) ce qui signifie que les charges de tension et de compression développées dans les brides de la branche sont transférées presque directement dans les parois latérales plus rigides de la corde. L’état limite de rendement local du flanc (équation AISC 360-10 K3-7) d’une connexion en T peut alors être dérivé de l’équation de rendement local du voile pour des forces concentrées appliquées à une distance de l’extrémité de l’élément supérieure à sa profondeur (équation AISC 360-10 J10-2) :

Mn = 0.5Fyt (Hb + 5t) 2
Équation 2

Pour le rendement local de la branche dû à une répartition inégale de la charge (équation AISC 360-10 K3-8) dans une connexion en T, une approche de la largeur effective est utilisée pour réduire la capacité de l’élément de contreventement pour obtenir le moment nominal appliqué par l’entretoise:

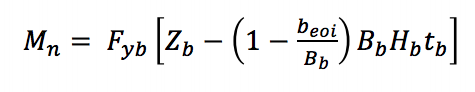
Fyb est la limite d’élasticité minimale spécifiée de la branche, Zb est le module de section plastique de la branche autour de l’axe de flexion, beoi est la largeur effective de la branche, Bb est la largeur hors tout de la branche et tb est l’épaisseur de paroi de conception de la branche.

Comme il existe peu de preuves expérimentales à l’appui de modèles de conception spécifiques pour les connexions en treillis de Vierendeel (connexions en T) en flexion hors plan, des états limites analogues à ceux de la flexion dans le plan sont utilisés (Packer et al. 2010). Un état limite supplémentaire de rupture de distorsion de corde se développe à partir du couple appliqué à la corde par l’organe de dérivation à la suite du moment hors plan. Ce couple peut entraîner une distorsion rhomboïdale de la corde. Les équations de moment nominal pour la flexion hors plan se trouvent dans les équations AISC 360-10 K3-9, K3-10, K3-11 et K3-12. Les équations pour la flexion dans le plan et hors du plan des connexions en T sont similaires à celles qui ont été adoptées au niveau international (Packer et al. 2010).

Les équations de conception ci-dessus ont été dérivées en considérant les systèmes de fermes Vierendeel sous charges statiques. Une étude récente (Fadden et al. 2015) a poursuivi ce travail pour examiner le comportement des connexions de moment HSS à HSS carrées et rectangulaires sous de grandes charges cycliques pour une utilisation dans des systèmes de trames de moment sismiques à base de tubes (trames de moment intermédiaires et spéciales). Un tel système cherche à tirer parti des excellentes propriétés axiales, de flexion et de torsion, du rapport résistance / poids élevé et du caractère architectural agréable des SSH carrés et rectangulaires. La résistance élevée à la torsion peut entraîner une réduction du contreventement latéral de la poutre, tandis que le rapport résistance / poids élevé se traduit par une masse sismique plus faible. Cependant, de telles connexions doivent pouvoir subir un accrochage plastique stable de l’élément de poutre où 80% de la capacité plastique de l’élément de poutre est maintenue à 0,2 rad. (FMI) ou 0,4 rad. (SMF) de la dérive inter-étages (AISC 341-10). Étant donné que la conception sismique actuelle des systèmes de trames de moment nécessite que la majorité du comportement inélastique se produise dans l’élément de poutre, l’élément de poutre doit également atteindre sa pleine capacité plastique avant de subir un flambage local. Fadden et McCormick (2014a) ont examiné des modèles expérimentaux et des modèles à éléments finis pour déterminer les exigences limites en largeur-épaisseur et en profondeur-épaisseur pour les SSH en flexion, car celles spécifiées dans les dispositions sismiques actuelles de l’AISC (AISC 341-10) ont été largement développées sur la base d’essais d’éléments SSH à charge axiale cyclique.

Pour déterminer les exigences de configuration et de détail appropriées pour répondre à cette demande de résistance et de ductilité, quatre configurations de connexion différentes ont été testées expérimentalement: deux connexions non renforcées soudées directement (non appariées et appariées) et deux connexions renforcées (plaque traversante et plaque de diaphragme externe). Toutes les connexions utilisaient une colonne HSS 10x10x5/8. Les connexions directement soudées utilisaient des soudures CJP préqualifiées telles que spécifiées dans AWS D1.1 (2010). Pour la connexion inégalée, le faisceau était un HSS 12x8x3/8 (β = 0.8) suggérant que la plastification de la face de la colonne peut être un problème. Pour la connexion adaptée, la poutre était un HSS 12x10x3/8 (β = 1,0) permettant de transférer les charges directement dans le flanc. Le protocole de chargement AISC pour la préqualification des connexions à moment sismique a été utilisé (AISC 341-10) pour charger les connexions. Le comportement des connexions a été tel que prévu, la connexion non appariée présentant une déformation à la face de la colonne, tandis que la connexion adaptée a pu transférer la charge sur les parois latérales de la colonne. Cependant, les deux connexions ont échoué en raison d’une fracture du métal de base de la colonne au bout du coin de la soudure (figure 3). Cette rupture fragile à des rotations de 0,4 rad. et 0,5 rad., respectivement, a confirmé que les connexions directement soudées ne fournissent pas le comportement approprié pour les applications sismiques.

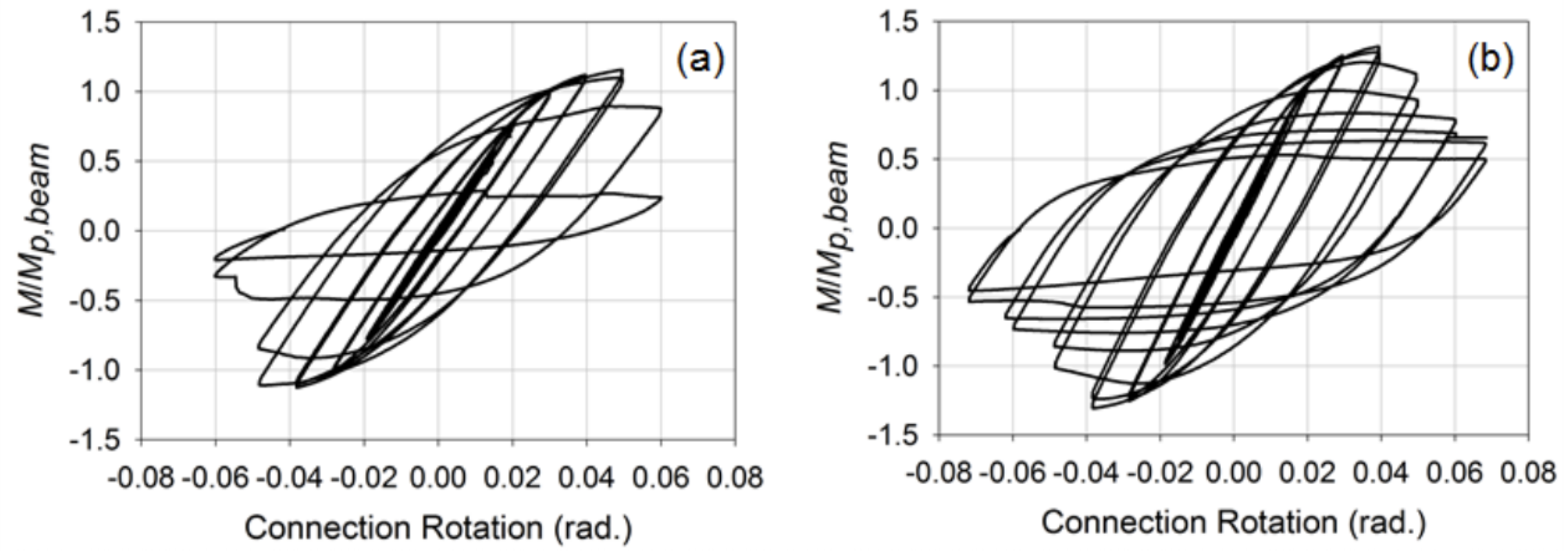
Les connexions renforcées ont ensuite été développées en tenant compte des plaques à membrane et des plaques de diaphragme externes qui sont souvent utilisées dans les connexions de colonne poutre-HSS à bride large afin de fournir un meilleur mécanisme pour transférer les forces de tension et de compression sur le flanc de la colonne et minimiser les concentrations de contraintes imposées aux soudures. Pour ces connexions, les faisceaux étaient des éléments HSS 12x8x3/8 (β = 0,8). Des informations sur la procédure spécifique utilisée pour concevoir et détailler ces connexions se trouvent dans Fadden et McCormick (2014b) et Fadden et al. (2015). Placées sous la même charge que les connexions non renforcées, les connexions ont montré un comportement plus stable, la charnière en plastique se trouvant à l’écart de la face de la colonne à l’extrémité de la plaque de diaphragme traversante ou externe (Figure 4). Les deux connexions ont également pu atteindre 0,4 rad. de rotation avant de subir un flambage local qui a entraîné une dégradation de la capacité de moment. Cependant, la fracture s’est amorcée au coin de la poutre HSS en raison d’un cycle à des niveaux de rotation importants de 0,7 rad. Une comparaison des courbes moment-rotation normalisées pour les connexions de plaque de diaphragme appariées et externes est visible à la figure 5. Dans l’ensemble, les connexions renforcées se sont révélées prometteuses pour l’utilisation de systèmes de trames de moment sismique HSS-à-HSS, mais des travaux supplémentaires sont nécessaires pour déplacer ces connexions vers une préqualification éventuelle.

AISC. (2010). « Dispositions sismiques pour les bâtiments en Acier de construction”. Norme ANSI/AISC 341-10. Institut américain de Construction en acier, Chicago, IL.

AISC. (2010). « Spécifications pour les bâtiments en acier de construction »” Norme ANSI/AISC 360-10. Institut américain de Construction en acier, Chicago, IL.

AWS. (2010). « Code de soudage structurel »” ANSI / AWS D1.1, Société américaine de soudage, Miami, Floride.

Fadden, F. et McCormick, J. (2014a). « Modèle par éléments Finis du Comportement de Flexion Cyclique des Sections Structurelles Creuses”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. et McCormick, J. (2014b). « Performance et conception de connexion de Moment sismique HSS-à-HSS”. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., et McCormick, J. (2015). « Essais Cycliques de Connexions de Moment HSS à HSS Soudées pour des applications sismiques »” ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J.E.M. et Redwood, R.G. (1966). « Conception des joints aux sections de Boîte »” The Institution of Structural Engineers, Conference on Industrialized Building et the Structural Engineer, Institute of Structural Engineers, Londres.

Korol, R.M., El-Zanaty, M., et Brady, F.J. (1977). « Connexions de Largeur Inégale de Sections Creuses Carrées dans des Fermes Vierendeel”. Revue canadienne de génie civil, 4, 190-201.

Packer, J.A. (1993). « Connexions de Moment entre les Sections Creuses Rectangulaires »” Journal of Constructional Steel Research, 25, 63-81.

Packer, J.A., Wardenier, J., Zhao, X.-L., van der Vegte, G.J. et Kurobane, Y. (2010). Guide de Conception 3: Pour les Joints à Section Creuse Rectangulaire (RHS) sous Chargement Principalement Statique 2e Édition. CIDECT, Canada.

Wardenier, J. (1982). « Joints À section creuse ». Presse universitaire de Delft, Delft, Pays-Bas.

Septembre 2016

Télécharger le PDF