Calculatrice Moyenne, Médiane, Mode, Plage
Veuillez fournir des nombres séparés par une virgule pour calculer.
Calculateur de statistiques connexes / Calculateur d’Écart-type / Calculateur de taille d’échantillon
Moyenne
Le mot mean, qui est un homonyme de plusieurs autres mots en langue anglaise, est également ambigu même dans le domaine des mathématiques. Selon le contexte, qu’il soit mathématique ou statistique, ce que l’on entend par » moyenne » change. Dans sa définition mathématique la plus simple concernant les ensembles de données, la moyenne utilisée est la moyenne arithmétique, également appelée espérance mathématique, ou moyenne. Sous cette forme, la moyenne fait référence à une valeur intermédiaire entre un ensemble discret de nombres, à savoir la somme de toutes les valeurs de l’ensemble de données, divisée par le nombre total de valeurs. L’équation pour calculer une moyenne arithmétique est pratiquement identique à celle pour calculer les concepts statistiques de moyenne de population et d’échantillon, avec de légères variations dans les variables utilisées:
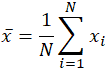
La moyenne est souvent notée x, prononcée « x bar », et même dans d’autres utilisations lorsque la variable n’est pas x, la notation en barres est un indicateur courant d’une certaine forme de moyenne. Dans le cas spécifique de la moyenne de la population, plutôt que d’utiliser la variable x, le symbole grec mu, ou μ, est utilisé. De même, ou plutôt de manière confuse, la moyenne de l’échantillon en statistique est souvent indiquée par un X majuscule. Compte tenu de l’ensemble de données 10, 2, 38, 23, 38, 23, 21, l’application de la somme ci-dessus donne:
|
10 + 2 + 38 + 23 + 38 + 23 + 21
|
= | =22.143 |
Comme mentionné précédemment, il s’agit de l’une des définitions les plus simples de la moyenne, et d’autres incluent la moyenne arithmétique pondérée (qui ne diffère que par le fait que certaines valeurs de l’ensemble de données apportent plus de valeur que d’autres) et la moyenne géométrique. Une bonne compréhension de situations et de contextes donnés peut souvent fournir à une personne les outils nécessaires pour déterminer la méthode statistiquement pertinente à utiliser. En général, la moyenne, la médiane, le mode et la plage devraient idéalement tous être calculés et analysés pour un échantillon ou un ensemble de données donné, car ils élucident différents aspects des données données et, s’ils sont pris en compte seuls, peuvent conduire à de fausses représentations des données, comme nous le démontrerons dans les sections suivantes.
Médiane
Le concept statistique de la médiane est une valeur qui divise un échantillon de données, une population ou une distribution de probabilité en deux moitiés. Trouver la médiane implique essentiellement de trouver la valeur dans un échantillon de données qui a un emplacement physique entre le reste des nombres. Notez que lors du calcul de la médiane d’une liste finie de nombres, l’ordre des échantillons de données est important. Classiquement, les valeurs sont répertoriées dans l’ordre croissant, mais il n’y a aucune raison réelle que la liste des valeurs dans l’ordre décroissant fournisse des résultats différents. Dans le cas où le nombre total de valeurs dans un échantillon de données est impair, la médiane est simplement le nombre au milieu de la liste de toutes les valeurs. Lorsque l’échantillon de données contient un nombre pair de valeurs, la médiane est la moyenne des deux valeurs intermédiaires. Bien que cela puisse prêter à confusion, rappelez-vous simplement que même si la médiane implique parfois le calcul d’une moyenne, lorsque ce cas se présente, elle n’impliquera que les deux valeurs moyennes, alors qu’une moyenne implique toutes les valeurs de l’échantillon de données. Dans les cas impairs où il n’y a que deux échantillons de données ou un nombre pair d’échantillons où toutes les valeurs sont identiques, la moyenne et la médiane seront les mêmes. Compte tenu du même ensemble de données que précédemment, la médiane serait acquise de la manière suivante:
2,10,21,23,23,38,38
Après avoir listé les données dans l’ordre croissant et déterminé qu’il existe un nombre impair de valeurs, il est clair que 23 est la médiane dans ce cas. S’il y avait une autre valeur ajoutée à l’ensemble de données:
2,10,21,23,23,38,38,1027892
Comme il existe un nombre pair de valeurs, la médiane sera la moyenne des deux nombres médians, dans ce cas 23 et 23, dont la moyenne est 23. Notez que dans cet ensemble de données particulier, l’ajout d’une valeur aberrante (une valeur bien en dehors de la plage de valeurs attendue), la valeur 1 027 892, n’a aucun effet réel sur l’ensemble de données. Si toutefois la moyenne est calculée pour cet ensemble de données, le résultat est de 128 505,875. Cette valeur n’est clairement pas une bonne représentation des sept autres valeurs de l’ensemble de données qui sont beaucoup plus petites et plus proches en valeur que la moyenne et la valeur aberrante. C’est le principal avantage de l’utilisation de la médiane pour décrire les données statistiques par rapport à la moyenne. Bien que les deux valeurs, ainsi que d’autres valeurs statistiques, doivent être calculées lors de la description des données, si une seule peut être utilisée, la médiane peut fournir une meilleure estimation d’une valeur typique dans un ensemble de données donné lorsqu’il existe des variations extrêmement importantes entre les valeurs.
Mode
En statistiques, le mode est la valeur d’un ensemble de données qui a le plus grand nombre de récurrences. Il est possible qu’un ensemble de données soit multimodal, c’est-à-dire qu’il comporte plusieurs modes. Par exemple :
2,10,21,23,23,38,38
23 et 38 apparaissent deux fois chacun, ce qui les rend tous deux un mode pour l’ensemble de données ci-dessus.
De même que la moyenne et la médiane, le mode est utilisé comme un moyen d’exprimer des informations sur des variables aléatoires et des populations. Contrairement à la moyenne et à la médiane, le mode est un concept qui peut être appliqué à des valeurs non numériques telles que la marque de chips de tortilla les plus couramment achetées dans une épicerie. Par exemple, en comparant les marques Tostitos, Mission et XOCHiTL, s’il s’avère que dans la vente de chips tortillas, XOCHiTL est le mode et se vend dans un rapport de 3: 2: 1 par rapport aux chips tortillas de marque Tostitos et Mission respectivement, le rapport pourrait être utilisé pour déterminer le nombre de sacs de chaque marque à stocker. Dans le cas où 24 sacs de chips tortillas se vendent pendant une période donnée, le magasin stockerait 12 sacs de chips XOCHiTL, 8 de Tostitos et 4 de Mission si vous utilisez le mode. Si toutefois le magasin utilisait simplement une moyenne et vendait 8 sacs de chacun, il pourrait potentiellement perdre 4 ventes si un client ne souhaitait que des puces XOCHiTL et pas une autre marque. Comme le montre cet exemple, il est important de prendre en compte toutes les manières de valeurs statistiques lorsque l’on tente de tirer des conclusions sur un échantillon de données.
Plage
La plage d’un ensemble de données dans les statistiques est la différence entre les valeurs les plus grandes et les plus petites. Bien que la plage ait des significations différentes dans différents domaines de la statistique et des mathématiques, c’est sa définition la plus fondamentale, et c’est ce qui est utilisé par la calculatrice fournie. En utilisant le même exemple:
2,10,21,23,23,38,38
38-2 =36
La plage dans cet exemple est de 36. De même que la moyenne, la plage peut être affectée de manière significative par des valeurs extrêmement grandes ou petites. En utilisant le même exemple que précédemment :
Leave a Reply