Énergétique de la Formation de liaisons ioniques

Des liaisons ioniques se forment lorsque des ions chargés positivement et négativement sont maintenus ensemble par des forces électrostatiques. Considérons une seule paire d’ions, un cation et un anion. Quelle sera la force de leur attraction? Selon la loi de Coulomb, l’énergie de l’attraction électrostatique (\(E\)) entre deux particules chargées est proportionnelle à l’amplitude des charges et inversement proportionnelle à la distance internucléaire entre les particules (\(r\)):

\

\

où la charge de chaque ion est représentée par le symbole Q. La constante de proportionnalité k est égale à 2,31 × 10-28 J *m. Cette valeur de k inclut la charge d’un seul électron (1,6022 × 10-19 C) pour chaque ion. L’équation peut également s’écrire en utilisant la charge de chaque ion, exprimée en coulombs (C), incorporée dans la constante. Dans ce cas, la constante de proportionnalité, k, est égale à 8,999 × 109 J *m/C2. Dans l’exemple donné, Q1 = +1 (1,6022 × 10-19 C) et Q2 = -1 (1,6022 × 10-19 C). Si Q1 et Q2 ont des signes opposés (comme dans NaCl, par exemple, où Q1 est + 1 pour Na + et Q2 est -1 pour Cl−), alors E est négatif, ce qui signifie que l’énergie est libérée lorsque des ions chargés de manière opposée sont réunis à une distance infinie pour former une paire d’ions isolée.

L’énergie est toujours libérée lorsqu’une liaison est formée et, par conséquent, elle nécessite toujours de l’énergie pour rompre une liaison.

Comme le montre la courbe verte dans la moitié inférieure de la figure \(\PageIndex{1}\), l’énergie maximale serait libérée lorsque les ions sont infiniment proches les uns des autres, à r = 0. Parce que les ions occupent l’espace et ont une structure avec le noyau positif entouré d’électrons, ils ne peuvent cependant pas être infiniment proches les uns des autres. À de très courtes distances, les interactions répulsives électron-électron entre électrons sur des ions adjacents deviennent plus fortes que les interactions attrayantes entre ions avec des charges opposées, comme le montre la courbe rouge dans la moitié supérieure de la figure \(\PageIndex{1}\). L’énergie totale du système est un équilibre entre les interactions attractives et répulsives. La courbe violette de la figure \(\PageIndex{1}\) montre que l’énergie totale du système atteint un minimum à r0, le point où les répulsions électrostatiques et les attractions sont exactement équilibrées. Cette distance est la même que la distance de liaison mesurée expérimentalement.

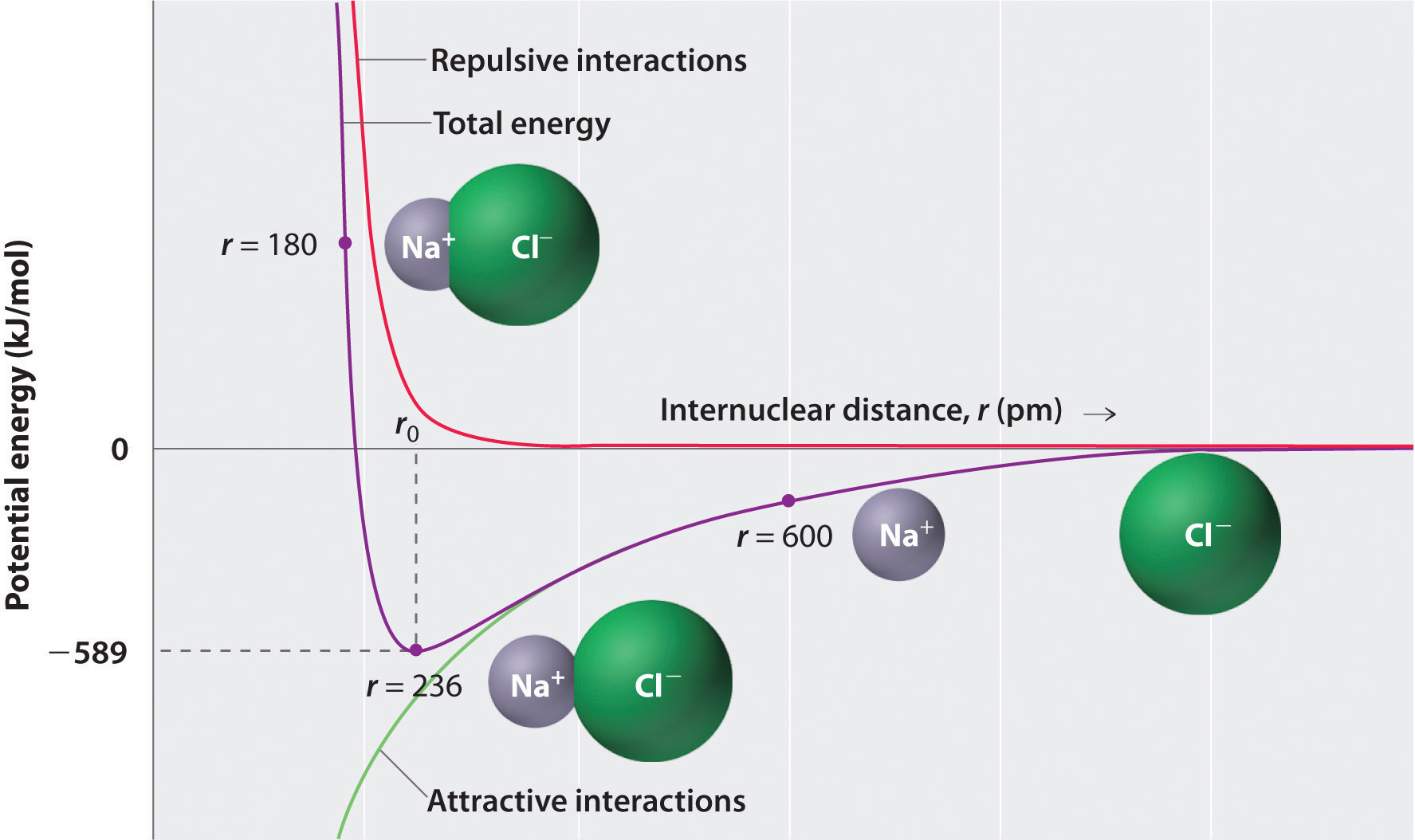
Considérons l’énergie libérée lorsqu’un ion gazeux \(Na^+\) et un ion gazeux \(Cl^-\) sont réunis de r=∞ à r=r0. Étant donné que la distance internucléaire observée en phase gazeuse est de 236 pm, le changement d’énergie associé à la formation d’une paire d’ions à partir d’un ion \(Na^+_{(g)}\) et d’un ion \(Cl^-_{(g)}\) est le suivant:

\&=(2,31\times{10^{-28}}\rm {J}\cdot\cancel{m})\ gauche (\dfrac{( + 1)( – 1)}{236\; \ annuler {pm}\ fois 10^{-12} \ annuler {m/pm}}\ droite) \\&=-9.79\times 10^{-19}\; J/ion\; pair\label{Eq2}\end{align*}\]

La valeur négative indique que de l’énergie est libérée. Notre convention est que si un processus chimique fournit de l’énergie au monde extérieur, le changement d’énergie est négatif. Si cela nécessite de l’énergie, le changement d’énergie est positif. Pour calculer le changement d’énergie dans la formation d’une mole de paires de NaCl, nous devons multiplier l’énergie par paire d’ions par le nombre d’Avogadro:

\

C’est l’énergie libérée lorsque 1 mole de paires d’ions gazeux se forme, et non lorsque 1 mole d’ions positifs et négatifs se condense pour former un réseau cristallin. En raison des interactions à longue portée dans la structure du réseau, cette énergie ne correspond pas directement à l’énergie du réseau du solide cristallin. Cependant, la grande valeur négative indique que le rapprochement des ions positifs et négatifs est énergétiquement très favorable, qu’il se forme une paire d’ions ou un réseau cristallin.

Nous résumons les points importants sur la liaison ionique:

• À r0, les ions sont plus stables (ont une énergie potentielle plus faible) qu’ils ne le sont à une distance internucléaire infinie. Lorsque des ions chargés de manière opposée sont réunis de r = ∞ à r = r0, l’énergie du système est abaissée (l’énergie est libérée).
• En raison de la faible énergie potentielle à r0, de l’énergie doit être ajoutée au système pour séparer les ions. La quantité d’énergie nécessaire est l’énergie de liaison.
• L’énergie du système atteint un minimum à une distance internucléaire particulière (la distance de liaison).