AUC-ROC – käyrä-Tähtisuorittaja!

olet rakentanut koneoppimismallisi – mitä seuraavaksi? Sinun täytyy arvioida sitä ja validoida, kuinka hyvä (tai huono) se on, joten voit sitten päättää, onko se toteuttaa. Siinä tulee AUC-ROC-käyrä.

nimi saattaa olla suupala, mutta se vain sanoo, että laskemme ”vastaanottimen Ominaisoperaattorin” (ROC) ”käyrän alle jäävää aluetta” (AUC). Hämmentynyt? Ymmärrän! Olen ollut kengissäsi. Mutta älä huoli, näemme, mitä nämä termit tarkoittavat yksityiskohtaisesti ja kaikki on helppo nakki!

toistaiseksi vain tietää, että AUC-ROC-käyrä auttaa meitä visualisoimaan, kuinka hyvin koneoppimisen luokittelijamme suoriutuu. Vaikka se toimii vain binary luokittelu ongelmia, näemme loppua kohti, miten voimme laajentaa sitä arvioida monen luokan luokittelu ongelmia liian.

käsittelemme aiheita, kuten herkkyyttä ja spesifisyyttä, koska nämä ovat keskeisiä aiheita AUC-ROC-käyrän takana.

ehdotan, että käymme läpi Sekaannusmatriisia käsittelevän artikkelin, koska siinä esitellään joitakin tärkeitä termejä, joita tulemme käyttämään tässä artikkelissa.

Sisällysluettelo

• Mitä ovat herkkyys ja spesifisyys?
• ennusteiden todennäköisyys
• mikä on AUC-ROC-käyrä?
• miten AUC-ROC-käyrä vaikuttaa?
• AUC-ROC Pythonissa
• AUC-ROC Moniluokkaluokituksessa

Mitä ovat herkkyys ja spesifisyys?

tältä näyttää sekaannusmatriisi:

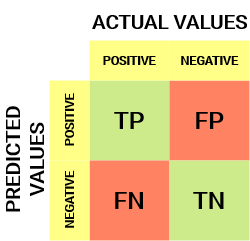
sekaannusmatriisista voidaan johtaa joitakin tärkeitä mittareita, joita ei käsitelty edellisessä artikkelissa. Puhutaan niistä täällä.

herkkyys / todellinen positiivinen osuus/takaisinkutsu

herkkyys kertoo, mikä osuus positiivisesta luokasta sai oikein luokituksen.

yksinkertainen esimerkki olisi selvittää, mikä osuus varsinaisista sairastuneista havaittiin oikein mallissa.

väärien negatiivisten yleisyys

väärien negatiivisten yleisyys (FNR) kertoo, mikä osuus positiivisista luokittajista sai luokituksen väärin.

korkeampi TPR ja alempi FNR on toivottavaa, koska haluamme luokitella positiivisen luokan oikein.

spesifisyys/todellinen negatiivinen yleisyys

spesifisyys kertoo, mikä osuus negatiivisesta luokasta sai oikein luokituksen.

kun otetaan sama esimerkki kuin herkkyydessä, spesifisyys tarkoittaisi sitä, että määriteltäisiin niiden terveiden ihmisten osuus, jotka mallilla tunnistettiin oikein.

väärän positiivisen yleisyys

FPR kertoo, mikä osuus negatiivisesta luokasta sai luokituksen väärin.

korkeampi TNR ja alempi FPR on toivottavaa, koska haluamme luokitella negatiivisen luokan oikein.

näistä mittareista herkkyys ja spesifisyys ovat ehkä tärkeimmät, ja näemme myöhemmin, miten näitä käytetään arviointimittarin rakentamiseen. Mutta sitä ennen ymmärretään, miksi ennustamisen todennäköisyys on parempi kuin kohdeluokan ennustaminen suoraan.

ennusteiden todennäköisyys

koneoppimisen luokittelumallia voidaan käyttää ennustamaan datapisteen todellinen luokka suoraan tai ennustamaan sen todennäköisyys kuulua eri luokkiin. Jälkimmäinen antaa meille enemmän kontrollia tulokseen. Voimme määrittää oman kynnyksemme tulkita luokittelijan tulosta. Tämä on joskus järkevämpää kuin pelkästään kokonaan uuden mallin rakentaminen!

erilaisten raja-arvojen asettaminen positiivisen luokan luokittelulle datapisteille muuttaa epähuomiossa mallin herkkyyttä ja spesifisyyttä. Ja yksi näistä kynnysarvoista antaa todennäköisesti paremman tuloksen kuin muut, riippuen siitä, onko tarkoitus vähentää väärien negatiivien vai väärien Positiivien määrää.

katso alla oleva taulukko:

metriikka muuttuu muuttuvien raja-arvojen myötä. Voimme luoda erilaisia sekaannusmatriiseja ja vertailla eri mittareita, joita käsittelimme edellisessä osiossa. Mutta se ei olisi viisasta. Sen sijaan, mitä voimme tehdä, on luoda tontin välillä joitakin näistä mittareista, jotta voimme helposti visualisoida, mikä kynnys antaa meille paremman tuloksen.

AUC-ROC-käyrä ratkaisee juuri tuon ongelman!

mikä on AUC-ROC-käyrä?

vastaanottimen operaattorin Ominaisuuskäyrä (Roc) on binääristen luokitteluongelmien arviointimetri. Se on todennäköisyyskäyrä, joka piirtää TPR: n FPR: ää vastaan eri raja-arvoilla ja erottaa olennaisesti ”signaalin” kohinasta. Käyrän alle jäävä pinta-ala (AUC) on luokittajan kykyä erottaa luokat toisistaan, ja sitä käytetään ROC-käyrän tiivistelmänä.

mitä suurempi AUC on, sitä parempi on mallin suorituskyky positiivisen ja negatiivisen luokan erottamisessa toisistaan.

kun AUC = 1, luokittelija pystyy täydellisesti erottamaan kaikki positiiviset ja negatiiviset luokkapisteet oikein. Jos kuitenkin AUC olisi ollut 0, luokittelija ennustaisi kaikki negatiiviset positiivisiksi ja kaikki positiiviset negatiivisiksi.

Kun 0.5<AUC<1, on suuri mahdollisuus, että luokittaja pystyy erottamaan positiiviset luokkaarvot negatiivisista luokkaarvoista. Tämä johtuu siitä, että luokittelija pystyy havaitsemaan enemmän numeroita tosi positiivisia ja tosi negatiivisia kuin vääriä negatiivisia ja vääriä positiivisia.

kun AUC=0, 5, luokittelija ei pysty erottamaan positiivisia ja negatiivisia luokkapisteitä. Eli joko luokittelija ennustaa satunnaisluokan tai Vakioluokan kaikille datapisteille.

eli mitä suurempi luokittajan AUC-arvo on, sitä paremmin se pystyy erottamaan positiivisen ja negatiivisen luokan toisistaan.

miten AUC-ROC-käyrä vaikuttaa?

ROC-käyrässä suurempi X-akselin arvo ilmaisee suuremman määrän vääriä positiivisia kuin todellisia negatiiveja. Kun taas suurempi Y-akselin arvo ilmaisee suuremman määrän todellisia positiivisia kuin vääriä negatiivisia. Kynnyksen valinta riippuu siis kyvystä tasapainottaa vääriä positiivisia ja vääriä negatiivisia.

kaivetaan hieman syvemmälle ja ymmärretään, miltä ROC-käyrämme näyttäisi eri raja-arvojen osalta ja miten spesifisyys ja herkkyys vaihtelevat.

voimme yrittää ymmärtää tätä kuvaajaa luomalla sekaannusmatriisin jokaiselle kynnystä vastaavalle pisteelle ja puhua luokittajamme suorituskyvystä:

piste A on missä herkkyys on suurin ja spesifisyys alhaisin. Tämä tarkoittaa, että kaikki positiiviset luokkapisteet luokitellaan oikein ja kaikki negatiiviset luokkapisteet väärin.

itse asiassa mikä tahansa piste sinisellä viivalla vastaa tilannetta, jossa todellinen positiivinen osuus on yhtä suuri kuin väärä positiivinen osuus.

Kaikki tämän viivan yläpuoliset pisteet vastaavat tilannetta, jossa oikein luokiteltujen positiiviseen luokkaan kuuluvien pisteiden osuus on suurempi kuin väärin luokiteltujen negatiiviseen luokkaan kuuluvien pisteiden osuus.

vaikka pisteellä B on sama herkkyys kuin pisteellä a, sillä on suurempi spesifisyys. Eli väärin negatiivisten luokkapisteiden määrä on pienempi verrattuna edelliseen kynnykseen. Tämä osoittaa, että tämä kynnysarvo on parempi kuin edellinen.

pisteiden C ja D välillä, herkkyys pisteessä C on suurempi kuin pisteessä D samalla spesifisyydellä. Tämä tarkoittaa, että luokittaja ennusti samalle määrälle väärin luokiteltuja negatiivisia luokkapisteitä suuremman määrän positiivisia luokkapisteitä. Siksi kynnys pisteessä C on parempi kuin pisteessä D.

nyt riippuen siitä, kuinka monta väärin luokiteltua pistettä haluamme sietää luokittelijallemme, valitsisimme pisteen B tai C välillä ennustaaksemme, voitteko päihittää minut PUBG: ssä vai ette.

”turhat toiveet ovat pelkoja vaarallisempia.”- J. R. R. Tolkein

Piste E on, missä spesifisyys tulee korkeimmaksi. Eli mallin luokittelemia vääriä positiivisia ei ole. Malli voi luokitella oikein kaikki negatiiviset luokkapisteet! Valitsisimme tämän kohdan, jos ongelmamme olisi antaa täydelliset laulusuositukset käyttäjillemme.

menee tällä logiikalla, osaatko arvata, missä kohtaa täydellistä luokittelijaa vastaava piste olisi kuvaajassa?

Yes! Se olisi ROC-kuvaajan vasemmassa yläkulmassa, joka vastaa karteesisen tason koordinaattia (0, 1). Tässä molemmat, herkkyys ja spesifisyys, olisivat korkeimpia ja luokittelija luokittelisi oikein kaikki positiiviset ja negatiiviset luokkapisteet.

Pythonin AUC-ROC-käyrän ymmärtäminen

nyt joko voimme manuaalisesti testata jokaisen kynnyksen herkkyyttä ja spesifisyyttä tai antaa sklearnin tehdä työn puolestamme. Valitsemme ehdottomasti jälkimmäisen!

luodaan mielivaltainen datamme sklearn make_luokitusmenetelmällä:

aion testata kahden luokittajan suorituskykyä tällä aineistolla:

Sklearnilla on erittäin tehokas menetelmä roc_curve (), joka laskee ROC: n luokittajallesi muutamassa sekunnissa! Se palauttaa FPR -, TPR – ja kynnysarvot:

AUC-pisteet voidaan laskea sklearnin roc_auc_score () – menetelmällä:

0.9761029411764707 0.9233769727403157

kokeile tätä koodia alla olevassa live-koodausikkunassa:

voimme myös piirtää ROC-käyrät kahdelle algoritmille matplotlibin avulla:

kuvaajasta käy ilmi, että logistisen Regression ROC-käyrän AUC on suurempi kuin KNN ROC-käyrän. Siksi voimme sanoa, että logistinen regressio teki parempaa työtä luokitellessaan positiivisen luokan aineistossa.

AUC-ROC Moniluokkaluokituksessa

kuten aiemmin sanoin, AUC-ROC-käyrä on vain binääriluokitusongelmille. Mutta voimme laajentaa sitä moniluokan luokittelu ongelmia käyttämällä yksi vs kaikki tekniikka.

joten, jos meillä on kolme luokkaa 0, 1 ja 2, Roc luokitusta 0 vastaan ei 0, eli 1 ja 2. ROC luokan 1 syntyy luokitteluna 1 vastaan ei 1, ja niin edelleen.

moniluokkaisten luokitusmallien ROC-käyrä voidaan määrittää seuraavasti:

Loppuhuomautukset

Toivottavasti tämä artikkeli on hyödyllinen ymmärrettäessä, kuinka tehokas AUC-ROC-käyrämittari on luokittajan suorituskyvyn mittaamisessa. Voit käyttää tätä paljon teollisuudessa ja jopa data science tai koneoppiminen hackathons. Paras tutustua siihen!

jatkaen suosittelisin seuraavia kursseja, joista on hyötyä datatieteen taidon rakentamisessa:

• Introduction to Data Science
• Applied Machine Learning

voit lukea myös tämän artikkelin Mobiilisovelluksestamme