El problema de los 4 colores es uno de los problemas matemáticos más famosos. Resistió la prueba durante más de cien años antes de sucumbir finalmente; al final, había una prueba válida, pero que dependía de más de mil horas de tiempo de computadora. La investigación de Jim Tilley sugiere que una simplificación dramática podría ser posible en última instancia. Ha descubierto una propiedad, el bloqueo de Kempe, que debe exhibir un contraejemplo mínimo al teorema de los 4 colores y ha formulado una conjetura, basada en extensas investigaciones, de que el diamante Birkhoff es la única configuración fundamental de bloqueo de Kempe.

La coloración de grafos consiste en asignar etiquetas, o colores, a los vértices de un objeto matemático conocido como grafo. El problema de los 4 colores proporcionó una de las motivaciones originales para el desarrollo de la teoría de grafos algebraicos. La coloración gráfica se utiliza en muchos problemas del mundo real, como minimizar conflictos al programar eventos deportivos, planificar horarios de exámenes y organizar planos de asientos, incluso para la colocación de cámaras de circuito cerrado de televisión en un edificio con muchas esquinas para minimizar el solapamiento de la cámara. También proporciona la base para los rompecabezas de Sudoku.

El problema de los 4 colores
Francis Guthrie, un estudiante del famoso matemático y lógico británico Augustus De Morgan, planteó el problema de los 4 colores en 1852. Formuló el problema con respecto a los mapas que cumplen ciertas condiciones, como no contener agujeros y tener todas las regiones (por ejemplo, país o estado) conectadas de modo que no exista ninguna región en dos o más partes no contiguas. Guthrie afirmó que para tales mapas nunca se necesitarían más de cuatro colores para colorear el mapa de manera que no hubiera dos regiones vecinas del mismo color.

Hoy en día, el problema de los 4 colores se expresa en términos de gráficos, y en lugar de colorear regiones en los mapas, uno colorea los vértices en los gráficos. Todas las pruebas existentes del teorema de los 4 colores demuestran que no puede existir un contraejemplo mínimo. (Un contraejemplo mínimo es el grafo plano más pequeño que requiere más de cuatro colores para una coloración adecuada de sus vértices.) Solo se deben considerar los gráficos planos que son triangulaciones, ya que cualquier gráfico que no es una triangulación se puede convertir en uno insertando bordes. Si la triangulación resultante es de 4 colores, entonces el gráfico original también es de 4 colores. Es muy útil poder restringir el escrutinio a triangulaciones.

Un primer intento de prueba
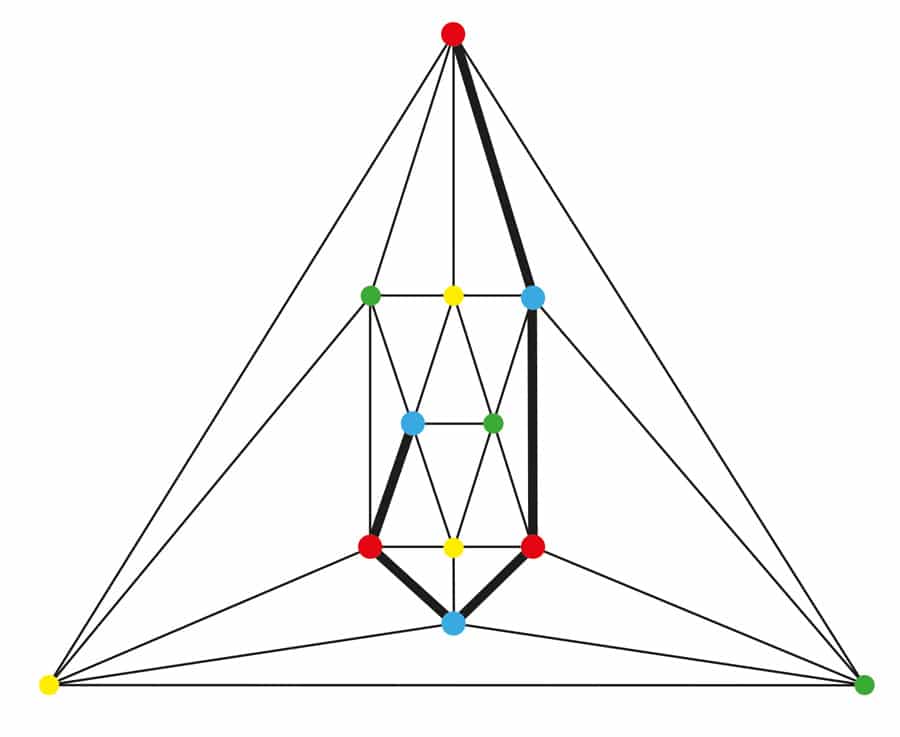
De aquellos que ofrecieron una prueba, Alfred Bray Kempe, un abogado inglés y matemático aficionado, fue la persona cuya reputación estaba más manchada por su esfuerzo fallido. Anunció su éxito en 1879 y su ‘prueba’ se publicó en el American Journal of Mathematics. Once años más tarde, sin embargo, otro matemático inglés, Percy Heawood, creó un mapa que coloreó en 4 colores hasta la región final de tal manera que el método de Kempe falló para esa región final. A pesar de su fracaso, Kempe dejó una herramienta útil: una cadena Kempe. Es un subgrafo máximo conectado (cada vértice accesible desde cualquier otro por un camino a lo largo de las aristas) en el que todos los vértices usan exactamente dos colores. Las cadenas Kempe han demostrado ser útiles para colorear y volver a colorear gráficos. Véase la Figura 1.

Sería una simplificación asombrosa
si el diamante Birkhoff por sí solo es la clave de la 4-colorabilidad.

Prueba por fin
La primera prueba válida fue anunciada en 1976 por Kenneth Appel y Wolfgang Haken. Requirió más de mil horas de tiempo de computadora para verificar aspectos particulares de su argumento. Esta noción de confiar en el código informático, que potencialmente contiene errores inducidos por el hombre (¡y su código sí!), en lugar de una prueba «humana», no ha satisfecho a una gran parte de la comunidad matemática. La prueba de Appel y Haken era elegante en su estructura general, pero los detalles eran feos.

La prueba fue refinada en 1996 por un equipo de cuatro matemáticos: Robertson, Sanders, Seymour y Thomas, pero todavía confiaban en el código de computadora para completar su prueba. En 2010, Steinberger ofreció otra variación. Sin embargo, todavía no hay una respuesta completamente satisfactoria de por qué el teorema de los 4 colores es cierto. (Una vez que la conjetura fue probada, ganó el estatus de teorema’.»)

La búsqueda de una prueba alternativa
El problema de los 4 colores es tan fácil de articular y comprender que ha atraído el interés de muchos miles de matemáticos aficionados, todos creyendo que pueden encontrar una prueba clásica simple y así hacerse famosos. El padre de Jim Tilley, físico y director del Real Colegio Militar de Canadá de 1978 a 1984, era uno de esos soñadores. Cada vez que sentía que había hecho un gran avance, le pedía a su hijo, Jim, que revisara su trabajo. Jim siempre encontraba un defecto. Sin embargo, a pesar de su escepticismo inicial de que los esfuerzos de su padre alguna vez darían fruto, se infectó con un entusiasmo por el problema de los 4 colores y comenzó a estudiarlo intensamente.

Kempe-locking
La investigación de Jim Tilley le llevó a descubrir una nueva propiedad que un contraejemplo mínimo al teorema de los 4 colores debe exhibir. Lo llamó Kempe-locking.»Se dio cuenta de que era probable que fuera incompatible con otra propiedad que un contraejemplo mínimo debía exhibirse, a saber., qué tan conectado está un gráfico (cuántos vértices deben eliminarse de un gráfico antes de que se desmorone).

El bloqueo Kempe de Tilley es una propiedad asociada con una arista en una triangulación. La noción comienza con la eliminación de una arista xy entre los vértices adyacentes x e y. Si por cada 4 colores del gráfico resultante en el que los colores de x e y son los mismos, no hay una secuencia de intercambios de colores en las cadenas de Kempe que haga que el color de x difiera del color de y, entonces se dice que la triangulación original está bloqueada por Kempe con respecto al borde xy. Tilley demostró que un contraejemplo mínimo para el teorema de los 4 colores tiene que ser bloqueado por Kempe con respecto a cada uno de sus bordes; cada borde en un contraejemplo mínimo debe tener esta propiedad de coloración.

El bloqueo de Kempe es una condición particularmente restrictiva que se vuelve más difícil de satisfacer a medida que una triangulación se hace más grande. Tilley se dispuso a descubrir si hay algo común en las triangulaciones que tienen bordes bloqueados por Kempe. Su primera búsqueda de Kempe-locking lo llevó al diamante Birkhoff.

El diamante Birkhoff
En 1913, G. D. Birkhoff descubrió que una cierta configuración de diez países en un mapa (un anillo de límites de seis países que encierra un conjunto de cuatro países) tiene una propiedad importante. Si esa configuración está presente en un mapa y si el submap con esa configuración eliminada es de 4 colores, entonces todo el mapa será de 4 colores. Por lo tanto, un contraejemplo mínimo no puede contener esa configuración en particular. Ha llegado a ser conocido como el diamante Birkhoff. Tilley descubrió que un borde bloqueado por Kempe xy parece surgir solo cuando x e y son también los puntos finales de la versión gráfica de un diamante Birkhoff. Véase la Figura 2.

La conjetura es fácil de establecer, comprensible e intrigante, y ofrece una explicación convincente de por qué todos los gráficos planos son de 4 colores.

Al no haber encontrado ninguna configuración de bloqueo de Kempe sin un diamante Birkhoff, conjeturó que el diamante Birkhoff es la única configuración de bloqueo de Kempe «fundamental», una que no contiene una configuración de bloqueo de Kempe más pequeña como subgrafo. Sin embargo, Tilley descubrió que no podía probar su conjetura crítica. Era frustrante porque, de ser verdad, la conjetura probaría directamente el teorema de los 4 colores. (Para ser un contraejemplo mínimo, una triangulación tendría que contener un subgrafo de diamante Birkhoff, pero si lo hiciera, no podría ser un contraejemplo mínimo.)

Un caso de apoyo abrumador En lugar de probar su conjetura, Tilley hizo lo siguiente mejor. Decidió jugar el papel de un experimentador y construir un caso abrumador para apoyar su conjetura. Dividió todas las triangulaciones planares relevantes en dos clases: aquellas en las que al menos cuatro vértices deben eliminarse antes de que los gráficos se rompan (4-conectados) y aquellas en las que al menos cinco vértices deben eliminarse antes de que los gráficos se rompan (5-conectados). Véase la Figura 3. Útil en la extensa búsqueda de Tilley fue que tuvo que examinar solo un miembro de cada clase de isomorfismo (gráficos que son estructuralmente idénticos). Tilley examinó las 8.044 clases de isomorfismo de triangulaciones planas de 4 conexiones en hasta 15 vértices y las 9.733 clases de isomorfismo de triangulaciones planas de 5 conexiones en hasta 24 vértices. Sólo encontró tres triangulaciones bloqueadas por Kempe. Cada borde bloqueado por Kempe descubierto presentaba un diamante Birkhoff y cada uno ocurría en una triangulación de 4 conexiones. No había ninguna entre 5 triangulaciones conectadas.

Tilley expandió su búsqueda entre 4 triangulaciones conectadas examinando las 30.926 clases de isomorfismo en 16 vértices y las 158.428 clases de isomorfismo en 17 vértices. Las limitaciones de tiempo de cálculo significaron restringir su búsqueda a muestras de 100.000 triangulaciones no isomórficas generadas aleatoriamente para cada clase en 18,19 y 20 vértices. La búsqueda expandida arrojó 45 triangulaciones adicionales bloqueadas por Kempe, pero exactamente los mismos resultados que la búsqueda original: cada borde bloqueado por Kempe en una triangulación presentaba un diamante Birkhoff asociado.

¿Desde dónde?
Las extensas búsquedas de Tilley confirmaron fácilmente que el diamante Birkhoff es una configuración fundamental de bloqueo de Kempe. Ha probado a fondo sus conjeturas, pero siguen sin probarse. Si (o cuando) la conjetura de Tilley se demuestra cierta, es decir, que el diamante Birkhoff por sí solo es la clave de la 4-colorabilidad, sería una simplificación asombrosa del problema: una configuración única que lo explica todo: elegancia matemática.

Probar la conjetura de 4 colores requirió los esfuerzos de muchos matemáticos prominentes. La conjetura de Tilley de que el diamante Birkhoff es la única configuración fundamental de bloqueo de Kempe puede ser aún más difícil de probar. Sin embargo, la evidencia experimental es fuerte. Los teóricos podrían decir ‘ ¿por qué molestarse?’La respuesta de Tilley es que la curiosidad insaciable ganará:» Después de todo, la conjetura es fácil de afirmar, comprensible e intrigante, y ofrece una explicación convincente de por qué todos los gráficos planos son de 4 colores.»