En las afueras de París, a ocho metros bajo tierra en una bóveda climatizada, se encuentra un cilindro de aleación de platino de 143 años de antigüedad. De solo 39 mm de altura, nunca ha sido tocado por manos humanas. Como una delicada muñeca rusa, el cilindro está enjaulado dentro de tres campanas de vidrio anidadas en una habitación a la que solo se puede acceder con tres llaves guardadas por tres personas diferentes. Alrededor del misterioso objeto están «los testigos»: seis cilindros» idénticos » fundidos de la misma aleación de platino.

Aunque los esfuerzos de preservación rivalizan con los del Sudario de Turín, el cilindro no es un objeto religioso sagrado. Es el Kilogramo Prototipo Internacional (IPK), el único kilogramo verdadero contra el que se miden todos los demás. Ubicado en el Pabellón de Breteuil, sede de la Oficina Internacional de Pesos y Medidas (BIPM), el IPK pronto perderá su estatus único y se convertirá en una reliquia de una época pasada. Entonces será tan pintoresco como el Metro Prototipo Internacional (IPM), una barra de aleación de platino que también se encuentra en el BIPM, que sirvió como el metro oficial del mundo hasta 1960.

El 16 de noviembre de 2018, metrólogos y responsables políticos de 60 países de todo el mundo se reunirán en la Conferencia General de Pesos y Medidas (CGPM) en Versalles, Francia. No hay nada inusual allí, ya que la reunión se reúne una vez cada cuatro años para discutir presupuestos y temas de metrología. Pero esta reunión será especial. Los Estados miembros votarán sobre la adopción del cambio más radical del Sistema Internacional de Unidades (Système International, o SI) desde su creación en 1960. Es un cambio que incluirá nuevas definiciones de kelvin, amperio y mol, pero quizás lo más significativo sea el kilogramo.

Cada Estado miembro emitirá su voto en un proceso que se transmitirá en vivo en línea. Si el cambio es ratificado (y todos los signos son que lo será), el evento marcará el fin de basar las unidades en objetos, una práctica que se remonta a milenios. También cumplirá finalmente un deseo expresado por primera vez por James Clerk Maxwell, quien predijo que los estándares de medición podrían definirse de alguna manera por constantes inmutables de la naturaleza.

Una base sólida

Hablando en una reunión de la Asociación Británica para el Avance de la Ciencia en Liverpool en 1870, Maxwell dijo a los delegados que «Si wish deseamos obtener estándares de longitud, tiempo y masa que sean absolutamente permanentes, debemos buscarlos no en las dimensiones, o el movimiento, o la masa de nuestro planeta, sino en la longitud de onda, el período de vibración y la masa absoluta de estas moléculas imperecederas e inalterables y perfectamente similares.»

Dado que los expertos no ven indicios de un resultado negativo en la reunión de BIPM de este mes, es seguro asumir que la resolución de reformar la IS pasará sin oposición y el deseo de Maxwell de estándares «absolutamente permanentes» se realizará. El nuevo SI entrará en vigor oficialmente el 20 de mayo de 2019, precisamente una docena de docenas (144) años después del primer tratado internacional sobre unidades de medida, la Convención del Metro, que se firmó el mismo día en 1875. Pero, ¿por qué es tan importante que las unidades se basen en constantes de la naturaleza?

Las unidades han sido un elemento básico de la sociedad desde al menos la época de los antiguos egipcios. Utilizaron diferentes partes del cuerpo humano u objetos de su entorno como escalas para medir las cosas. Sin embargo, estas normas podrían ser muy diferentes de un lugar a otro. Para los filósofos naturales de la Europa de los siglos XVII y XVIII, la variabilidad de unidades, particularmente en longitud y masa, hacía casi imposible comparar los resultados para el mismo fenómeno físico si se había medido en diferentes lugares.

Se hicieron varios intentos para crear una medida universal y en 1799 Francia introdujo el sistema métrico, basado en dos unidades: el metro y el kilogramo. Conocidos como el Metro de los Archivos y el Kilogramo de los Archivos, estos dos artefactos de platino se almacenaron en los Archives Nationales de París para definir legal y prácticamente las unidades. Estos estándares se mantuvieron durante 90 años hasta que fueron reemplazados por el IPM y el IPK, que eran físicamente más duros y mejor diseñados.

Pensamiento universal

Las unidades SI se han entrelazado en la ciencia. Desde el joule que define la energía hasta el katal para medir la actividad catalítica, las 29 unidades SI nombradas se pueden definir mediante una combinación de solo siete unidades básicas: la segunda, el metro, el kilogramo, el amperio, el kelvin, el mole y la candela. Pero a medida que la ciencia se hizo cada vez más precisa en el siglo XX, un nuevo problema surgió. Cualquier unidad basada en algo – un objeto, experimento o fenómeno – que no es universal será inestable.

Considere el segundo. Está históricamente vinculado a la revolución de la Tierra, que se define como la toma de 24 horas, donde una hora es de 60 minutos, y un minuto es de 60 segundos. Pero, ¿qué sucede si la Tierra comienza a girar más lentamente, como lo está haciendo aunque sea ligeramente? Un día será más largo, lo que significa que un segundo también será más largo en términos reales. Significa que un coche que registra 30 km / h viajará un poco más lento, una bombilla de 30 W será un poco más tenue y, lo que es más absurdo, el universo se expandirá a un ritmo diferente.

Si, sin embargo, la noción y la duración de un segundo se mantienen, pero la rotación de la Tierra se elimina de la definición y se reemplaza con algo que nunca cambia donde y cuando se mide en el universo, el segundo se vuelve estable. Esto se hizo en 1967, cuando el segundo fue redefinido como 9,192,631,770 veces el período de radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio-133, Δν (ver «Breve historia del mantenimiento del tiempo» de Helen Margolis).

Más tarde, en 1983, el metro también se redefinió, como la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de 1/299,792,458 segundos. La exquisita precisión con la que los científicos han podido medir desde entonces el tiempo y la distancia ha beneficiado a la sociedad, en particular al crear sistemas de determinación de la posición basados en satélites, en particular el GPS.

Planck al rescate

A pesar de haber servido bien a la sociedad durante 143 años, definir el kilogramo en términos de un solo objeto es una noción inherentemente inestable. Esto se debe a que si el IPK se vuelve más ligero o más pesado, incluso en una pequeña cantidad, la masa del universo expresada en kilogramos también cambia, una propuesta loca. Bastante preocupante, el IPK ha estado cambiando. Cuando los metrólogos lo midieron en 1988-1991, el IPK tenía una masa de alrededor de 50 µg menos en promedio que los seis testigos. Por definición, esto significa que los testigos habían ganado una pequeña cantidad de masa de alguna manera, tal vez absorbiendo moléculas de aire. Pero lo más probable, dado que muchas copias nacionales del kilogramo también parecían estar ganando masa, es que el IPK había perdido masa. O tal vez todos habían ganado o perdido masa, solo que a diferentes ritmos.

Los metrólogos no vieron más deriva entre el IPK y los testigos desde 1991 hasta 2014, la última vez que se hicieron las mediciones. Pero el hecho de que no hubiera deriva no significaba que la masa del IPK o de los testigos no hubiera cambiado. Es posible que simplemente hayan estado perdiendo o ganando masa en tándem. Y ese es el problema: no hay forma de saberlo porque la masa siempre está calibrada contra el IPK.

«Con el SI revisado, no tendremos que preocuparnos por estas cosas», explica Richard Davis, ex jefe de la división de masas de la BIPM que ahora es consultor de la oficina. En lugar de ser definido por la masa de un cilindro de metal, en el nuevo SI el kilogramo se basará en una constante fundamental de la física cuántica: la constante de Planck.

Lleva el nombre de Max Planck, quien desarrolló la idea de que la energía viene en pequeños paquetes llamados cuantos, la constante de Planck, h, relaciona la energía de un cuántico de radiación electromagnética con su frecuencia mediante la famosa fórmula E = hv. La constante de Planck está a su vez vinculada a la masa a través de la E = mc2 de Einstein. Actualmente, h tiene un valor medido de aproximadamente 6,62607 × 10-34 m2 kg s–1, pero los metrólogos ahora quieren fijar su valor en piedra, con el kilogramo definido en términos de este valor.

Por lo tanto, será adiós al IPK, que es un objeto físicamente inestable, y adiós a la incertidumbre en el valor de la constante de Planck. «Después de la redefinición, la constante inquebrantable de Planck se fija a un valor, mientras que la incertidumbre se desvía más apropiadamente a la masa del IPK», dice Stephan Schlamminger, un metrólogo del Instituto Nacional de Estándares y Tecnología de Estados Unidos. «Y con una tabla fija constante, mejores dispositivos podrán realizar un kilogramo cada vez con más precisión.»

Watt quiere decir

Para comenzar con el pie derecho, es importante que el valor al que se fija la constante de Planck se mida con la mayor precisión posible actualmente. Esta responsabilidad se basa en mediciones de dos tipos de experimentos muy diferentes. El primero de ellos se llama balanza de croquetas, anteriormente llamada balanza de vatios, pero ahora se le cambia el nombre en honor a su inventor Bryan Kibble, del Laboratorio Nacional de Física del Reino Unido, que murió en 2016. Actualmente, solo Francia, Canadá y los Estados Unidos tienen balanzas de croquetas capaces de hacer las mediciones necesarias para fijar la constante de Planck. Sin embargo, muchos otros están trabajando en construir balances propios. Al igual que un juego de básculas de alta tecnología, la balanza de Croquetas utiliza fuerzas electromagnéticas proporcionadas por una bobina de alambre sumergida en un campo magnético para equilibrar un kilogramo de masa. El equipo permite a los metrólogos tomar valores precisos de corriente y voltaje, de los que se puede derivar la constante de Planck (consulte el cuadro a continuación).

La Croqueta balance

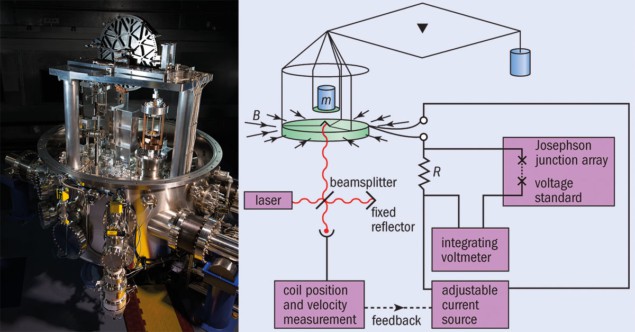
¿Qué es? La balanza de croquetas (o vatios) consiste en una bobina circular y horizontal de alambre de longitud, en L, colgado de un brazo de una balanza. La bobina se coloca en un campo magnético fuerte, B, y una corriente eléctrica, I, pasa a través de ella generando una fuerza, F = BIL, que se puede ajustar para igualar el peso de una masa colocada en el mismo brazo de la balanza (mg). La masa viene dada por m = BIL / g.

¿Cuál es el problema? Aunque se puede medir con precisión, es difícil hacer lo mismo para B y L.

Entonces, ¿cuál es la solución? Los metrólogos extraen la masa y mueven la bobina a velocidad u en el campo magnético para generar un voltaje V = BLu. El dispositivo se denomina equilibrio de vatios porque, al reorganizar las dos ecuaciones, la potencia eléctrica (VI) se equilibra con la potencia mecánica (mgu). En otras palabras, m = VI / gu. Como u es fácil de medir y g (la aceleración debida a la gravedad) es bien conocida, los problemas con la medición de B y L han desaparecido.

Pero, ¿cuál es el vínculo con la constante de Planck, h? Esa es la parte inteligente. La corriente se determina pasándola a través de una resistencia y usando el efecto Josephson para medir la caída de voltaje resultante. Este efecto describe el hecho de que si dos superconductores están separados por un aislante delgado, pares de electrones en cada capa se acoplan de modo que la radiación de microondas de frecuencia, f, crea un voltaje a través de la capa de V = hf/2e, donde e es la carga en el electrón. La resistencia de la resistencia se puede medir porque el flujo de electrones en sistemas 2D a temperaturas ultrabajas está cuantizado, y la conductividad aumenta en múltiplos de e2/h.

¿Por qué es bueno esto para la metrología? Hasta ahora, una balanza de croquetas medía h en unidades SI. Pero cuando se cambia la definición del kilogramo, el valor numérico de h se fija en piedra, lo que permite a cualquiera usar la balanza para medir la masa con una precisión exquisita.

La segunda forma de medir h se llama Densidad de cristal de rayos X (XRCD) o el experimento Avogadro. Se trata de un cristal uniforme de átomos de silicio-28 que se ha mecanizado en una esfera casi redonda de 1 kg. Usando interferometría óptica, los metrólogos calculan primero el diámetro total – y por lo tanto el volumen – de la esfera. Luego, al combinar la interferometría óptica con el análisis de rayos X, pueden calcular el espaciado entre átomos, el volumen que ocupa cada uno y, por lo tanto, el número total de átomos en la esfera. Finalmente, al pesar la esfera, pueden determinar la constante de Avogadro. Este enfoque define cuántos átomos o moléculas hay en un mol de una sustancia, una cantidad bastante diferente a la masa, que ahora definirá el mol en sí. Una ecuación de la física atómica que une las constantes de Avogadro y Planck permite capturar un valor preciso de esta última.

Los laboratorios de todo el mundo han utilizado estas dos técnicas diferentes para medir la constante de Planck con una precisión extraordinaria para obtener un valor final acordado de 6.626, 070,150 × 10-34 kg m2 s–1,con una incertidumbre relativa de solo 10 partes por mil millones (2018 Metrologia 55 L13). Como por la constante de Avogadro, se fija en 6.022,140,76 × 1023 mol–1. Y una vez que se fijan las constantes de Planck y Avogadro, los complejos experimentos de los que se derivaron se pueden usar como estándares para medir un kilogramo y un mol.

Impacto práctico

La forma más fácil de explicar cómo funcionará esto es considerar el equilibrio de Croquetas. Hasta ahora, se ha utilizado para medir valores precisos de corriente y voltaje que luego se conectan a ecuaciones para obtener la constante de Planck. En el futuro, la constante de Planck será un valor fijo y esas mismas mediciones producirán la masa en la balanza. En otras palabras, cualquier persona con acceso a una balanza de croquetas puede obtener un kilogramo perfecto. El mismo principio se aplicará también al amperio y al kelvin, que en el futuro se darán en términos de carga en un electrón, e, y la constante de Boltzmann, k, respectivamente. Los equipos diseñados para medir con precisión estas constantes fundamentales ahora se girarán en la cabeza para realizar con precisión las unidades de amperio y kelvin (consulte el cuadro a continuación). En cuanto al metro, el segundo y la candela, sus definiciones se modificarán, pero permanecerán sin cambios.

Fuera de la metrología, el nuevo SI tendrá pocas consecuencias prácticas inmediatas y pasará desapercibido para la mayoría de las personas. Después de todo, las unidades pueden definirse de manera diferente, pero el objetivo es siempre mantener su tamaño igual. Sin embargo, definir el kilogramo, kelvin, amperio y mole de formas completamente nuevas basadas en constantes de la naturaleza los hace invariables, accesibles y prácticos. Por lo tanto, los científicos podrán medirlos en cualquier lugar, momento y escala.

«Por primera vez, podremos medir cantidades pequeñas y grandes con la misma precisión, ya que a las constantes fundamentales no les importa una escala», añade Schlamminger. Esto es importante. Antes de redefinir el metro, la longitud solo se podía medir con mucha precisión alrededor de un metro. Pero desde su redefinición, las aplicaciones de alta precisión, como la microelectrónica, se han beneficiado enormemente de la precisión con la que pueden medir la distancia a pequeñas escalas.

Del mismo modo, el nuevo kilogramo permitirá medir un kilogramo, gramo y miligramo con idéntica precisión, incluso hasta el punto de que las masas atómicas se medirán en kilogramos. Mientras exista una conexión experimental con la constante de Planck, se podrá medir la masa. Por lo tanto, los metrólogos están compitiendo para construir balanzas de mesa y nuevos dispositivos que miden la masa exactamente a escalas grandes y pequeñas. Por lo tanto, la nueva unidad de masa y las unidades SI generalmente son finalmente aptas para el siglo XXI, y permanecerán por mucho tiempo en el futuro. Como concluye acertadamente Schlamminger: «El nuevo SI es una construcción de belleza y lógica.»

• Para obtener más información sobre las nuevas definiciones de SI, consulte el libro electrónico gratuito de Descubrimiento del Mundo de la Física Redefiniendo el Kilogramo y otras unidades de SI de Stephan Schlamminger en www.physicsworlddiscovery.org