Secuencia de Fibonacci
La secuencia de Fibonacci es la serie de números:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
El siguiente número se encuentra sumando los dos números anteriores:
- el 2 se encuentra sumando los dos números anteriores (1 + 1),
- el 3 se encuentra sumando los dos números anteriores (1+2),
- el 5 es (2+3),
- y así sucesivamente!
Ejemplo: el siguiente número en la secuencia de arriba es 21 + 34 = 55
¡Es así de simple!
Aquí hay una lista más larga:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
¿Puedes averiguar los siguientes números?
Hace una Espiral
Cuando hacemos cuadrados con esos anchos, obtenemos una bonita espiral:
¿Ves cómo los cuadrados encajan perfectamente juntos?
Por ejemplo, 5 y 8 hacen 13, 8 y 13 hacen 21, y así sucesivamente.

Esta espiral se encuentra en la naturaleza!
Ver: La Naturaleza,La Proporción Áurea y Fibonacci
La Regla
La Secuencia de Fibonacci se puede escribir como una «Regla» (ver Secuencias y Series).
Primero, los términos están numerados de 0 en adelante de la siguiente manera:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Por lo que el término número 6 se llama x6 (que es igual a 8).
|
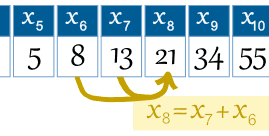
Ejemplo: el 8 de término es x8 = x7 + x6 |
 |
Así que podemos escribir la regla:
La Regla es xn = xn−1 + xn−2
donde:
- xn es el término número «n»
- xn−1 es el término anterior (n−1)
- xn−2 es el término antes de que (n−2)
Ejemplo: plazo 9 se calcula de la siguiente manera:
Cociente de Oro
Y aquí es una sorpresa. Cuando tomamos dos números de Fibonacci sucesivos (uno tras otro), su relación es muy cercana a la Relación Áurea «φ» que es aproximadamente 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
No tenemos que empezar con 2 y 3, aquí elegí al azar 192 y 16 (y obtuve la secuencia 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
Se tarda más en obtener buenos valores, pero muestra que no solo la secuencia de Fibonacci puede hacer esto!
Usando la Proporción Áurea para Calcular Números de Fibonacci
Y aún más sorprendente es que podemos calcular cualquier Número de Fibonacci usando la Proporción Áurea:
xn = φn – (1-φ)n√5
La respuesta sale como un número entero, exactamente igual a la suma de los dos términos anteriores.
Ejemplo: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
Cuando utilicé una calculadora en esto (solo ingresando la Proporción áurea a 6 decimales) Obtuve la respuesta 8.00000033 , un cálculo más preciso estaría más cerca de 8.
Pruebe n=12 y vea lo que obtiene.
También puede calcular un Número de Fibonacci multiplicando el Número de Fibonacci anterior por la Proporción Áurea y luego redondeando (funciona para números por encima de 1):
Ejemplo: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (redondeado)
Algunas cosas interesantes
Aquí está la secuencia de Fibonacci de nuevo:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Hay un patrón interesante:
- Mira el número x3 = 2. Cada 3er número es un múltiplo de 2 (2, 8, 34, 144, 610, …)
- Mira el número x4 = 3. Cada 4º número es un múltiplo de 3 (3, 21, 144, …)
- Mira el número x5 = 5. Cada 5º número es un múltiplo de 5 (5, 55, 610, …)
Y así sucesivamente (cada enésimo número es un múltiplo de xn).
1/89 = 0,011235955056179775…
Observe que los primeros dígitos (0,1,1,2,3,5) son la secuencia de Fibonacci?
En una forma en que todos, a excepción de varios números de un dígito (13, 21, etc) se superponen, como este:
… sucesivamente …
0.011235955056179775… = 1/89
Términos por Debajo de Cero
La secuencia de obras por debajo de cero también, como este:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(probarte a ti mismo que cada número es la suma de los dos números antes!)
De hecho, la secuencia por debajo de cero tiene los mismos números que la secuencia por encima de cero, excepto que siguen un+ -+ -… patrón. Puede ser escrita así:
x−n = (-1)n+1 xn
que dice que el término «n» es igual a (-1)n+1 veces término «n», y el valor (-1)n+1 hábilmente hace que el correcto +1, -1, +1, -1, … patrón.
Historia
Fibonacci no fue el primero en conocer la secuencia, ¡se conocía en la India cientos de años antes!

Sobre Fibonacci El Hombre
Su nombre real era Leonardo Pisano Bogollo, y vivió entre 1170 y 1250 en Italia.
«Fibonacci» era su apodo, que aproximadamente significa «Hijo de Bonacci».
Además de ser famoso por la Secuencia de Fibonacci, ayudó a difundir números arábigos Hindúes (como nuestros números actuales 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) a través de Europa en lugar de Números romanos (I, II, III, IV, V, etc.). ¡Eso nos ha ahorrado a todos muchos problemas! Gracias Leonardo.

Fibonacci Día
Fibonacci Día 23 de noviembre, ya que tiene los dígitos «1, 1, 2, 3», que es parte de la secuencia. Así que el próximo 23 de noviembre, ¡que todos lo sepan!


Leave a Reply