Revista beanz
Mapa de Merian-Erben (1652) en Wikipedia
El rompecabezas matemático de este mes se remonta a 1735, cuando fue resuelto por primera vez por Leonhard Euler, un matemático y físico suizo.
El rompecabezas se llama Los Siete Puentes de Königsberg. Se basa en una ciudad real, entonces en Prusia, ahora Kaliningrado en Rusia. La ciudad está dividida por un río con dos islas en el medio y, más abajo, el río divide la ciudad de nuevo.
El problema es engañosamente simple: hay (o había, en la época de Euler) siete puentes para conectar las dos islas y las partes aguas abajo de la ciudad. Euler se preguntó si una persona podría cruzar cada uno de los siete puentes una sola vez para tocar cada parte de la ciudad. Comenzar y terminar en el mismo lugar no era un requisito.
Aquí es un mapa que puede utilizar para intentar resolver el problema por sí mismo:
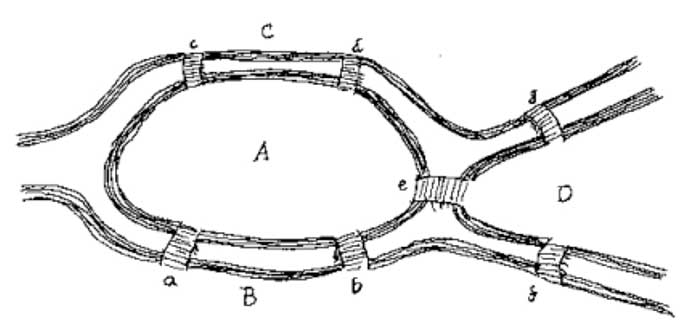
¿cuál crees Que es más importante para resolver este problema: el número de puentes o la ubicación de cada puente?
Respuesta: el número de puentes.
Euler demostró que el número de puentes debe ser par, por ejemplo, seis puentes en lugar de siete, si desea caminar sobre cada puente una vez y viajar a cada parte de Königsberg. La solución ve cada puente como un punto final, un vértice en términos matemáticos y las conexiones entre cada puente (vértice). Euler se dio cuenta de que solo un número par de puentes producía el resultado correcto de poder tocar cada parte de la ciudad sin cruzar un puente dos veces.
Euler utilizó las matemáticas para demostrar que era imposible cruzar los siete puentes una sola vez y visitar cada parte de Königsberg. Al hacerlo, puso en marcha una serie de descubrimientos e ideas sobre cómo se pueden definir el espacio y los espacios que se cruzan, así como sus propiedades. Una descripción detallada de la solución de Euler en el enlace de Wikipedia debajo de este artículo.
Si alguna vez has visto una tira de mobius, por ejemplo, has visto un ejemplo de topología, un campo de estudio matemático que evolucionó de la solución de Euler a este problema. La topología se refiere al espacio y a cómo las cosas se conectan entre sí, así como a la continuidad y los límites del espacio. La topología también estudia cómo las propiedades de un espacio cambian y no cambian cuando el espacio se expande o contrae.
En computación, la topología es útil para comprender las redes (rutas) que los datos pueden fluir dentro de cualquier sistema, así como cómo los conjuntos de datos pueden relacionarse entre sí. Los Siete Puentes de Königsberg también es similar a otro problema informático común llamado a veces el Problema del Vendedor Ambulante, donde se intenta encontrar la ruta más eficiente dado un conjunto de restricciones como los siete puentes en el problema de Euler.
Los no matemáticos (probablemente tú, definitivamente yo) experimentan el problema de los vendedores ambulantes cada vez que subimos a un tren o autobús. El Problema del Vendedor Ambulante es encontrar la forma más eficiente de viajar entre pares de ciudades de distancias especificadas. La gestión de recursos escasos (trenes, autobuses) que viajan a lo largo de rutas finitas es un problema perfecto para la computación, ya que las computadoras son más rápidas y eficientes. Pero primero necesitamos que Euler y otros expongan el problema y definan soluciones con matemáticas. Luego programamos nuestras computadoras para hacer los cálculos.
La topología también se ocupa de la teoría de conjuntos, cómo los grupos de cosas se pueden clasificar en conjuntos para identificar elementos comunes con otros grupos, así como elementos únicos. Un diagrama de Venn es un gran ejemplo de un conjunto. Y la programación a veces tiene que ordenar los datos de diferentes maneras. El método de clasificación que funciona mejor para una situación se puede determinar mediante la teoría de conjuntos.
¿Y qué pasó con los siete puentes de la época de Euler? Dos de ellos no sobrevivieron a la Segunda Guerra Mundial. Dos puentes fueron demolidos y reemplazados por una sola carretera. De los tres puentes restantes, uno fue reconstruido en 1935, mientras que los otros dos permanecen intactos como los conocía Euler. Y, por supuesto, Königsberg, Prusia, ha cambiado su nombre a Kaliningrado, Rusia.
Leave a Reply