El gráfico de una desigualdad lineal en una variable es una recta numérica. El uso de un círculo abierto para < y > y un círculo cerrado para ≤ y ≥.

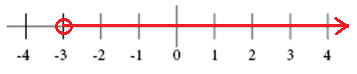
La gráfica para x > -3

La gráfica para x ≥ 2

las Desigualdades que tienen la misma solución se llaman equivalentes. Hay propiedades de desigualdades, así como también hay propiedades de igualdad. Todas las propiedades a continuación también son válidas para desigualdades que implican ≥ y ≤.

La propiedad de suma de la desigualdad dice que agregar el mismo número a cada lado de la desigualdad produce una desigualdad equivalente

If If \: x>y,\: then\: x+z>y+z

If If\: x<y,\: entonces\: x + z< y + z The

La propiedad de sustracción de la desigualdad nos dice que restar el mismo número de ambos lados de una desigualdad da una desigualdad equivalente.

If If \: x>y,\: then\: x-z>y-z

If If\: x<y,\: then\: x-z<y-z

La propiedad de multiplicación de la desigualdad nos dice que la multiplicación en ambos lados de una desigualdad con un número positivo produce una desigualdad equivalente.

If If\: x >y\: y\: z>0,\:, a continuación,\: xz>yz$$

$$ $ Si\: x<y\: y\: z>0,\:, a continuación,\: xz<yz$$

la Multiplicación en cada lado de una desigualdad con un número negativo por otro lado no producir un equivalente de la desigualdad a menos que también se invierte el sentido de la desigualdad símbolo

$$ $ Si \: x>y \: y\: z<0,\ :, a continuación,\: xz<yz$$

$$ $ Si\: x<y\: y\: z< 0,\: then\: xz> yz

Lo mismo ocurre con la propiedad de división de la desigualdad.

La división de ambos lados de una desigualdad con un número positivo produce una desigualdad equivalente.

$$ $ Si \: x>y \: y\: z>0,\:, a continuación,\: \frac{x}{z}>\frac{y}{z}$$

$$ $ Si\: x<y\: y\: z>0,\:, a continuación,\: \frac{x}{z}<\frac{y} {z}

Y la división en ambos lados de una desigualdad con un número negativo produce una desigualdad equivalente si el símbolo de desigualdad se invierte.

$$ $ Si \: x>y \: y\: z<0,\:, a continuación,\: \frac{x}{z}<\frac{y}{z}$$

$$ $ Si\: x<y\: y\: z<0,\:, a continuación,\: \frac{x}{z}>\frac{y}{z}$$

Para resolver un multi-paso de la desigualdad que hacer como hizo cuando la resolución de ecuaciones de varios pasos. Tome una cosa a la vez preferiblemente comenzando por aislar la variable de las constantes. Al resolver desigualdades de varios pasos, es importante no olvidar revertir el signo de desigualdad al multiplicar o dividir con números negativos.

Ejemplo

Resolver la desigualdad

$$-2\left ( x+3 \right )<10$$