Articles

Permutaciones y Combinaciones fáciles

by admin

Siempre he confundido «permutación» y «combinación» — ¿cuál es cuál?

Esta es una manera fácil de recordar: la permutación suena complicada, ¿no? Y lo es. Con permutaciones, cada pequeño detalle importa. Alice, Bob y Charlie es diferente de Charlie, Bob y Alice (inserta los nombres de tus amigos aquí).Las combinaciones

, por otro lado, son bastante fáciles de usar. Los detalles no importan. Alice, Bob y Charlie es lo mismo que Charlie, Bob y Alice.

Las permutaciones son para listas (el orden importa) y las combinaciones son para grupos (el orden no importa).

Ya sabes, un» bloqueo de combinación «debería llamarse» bloqueo de permutación». El orden en el que pones los números importa.

Permutaciones y combinaciones fáciles

Un «bloqueo de combinación» verdadero aceptaría tanto 10-17-23 como 23-17-10 como correctos.

Permutaciones: Los detalles peludos

Comencemos con las permutaciones, o todas las formas posibles de hacer algo. Estamos usando el término de pantalones elegantes «permutación», por lo que nos preocuparemos por cada detalle, incluido el orden de cada artículo. Digamos que tenemos 8 personas:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

¿De cuántas maneras podemos otorgar un premio de 1er, 2do y 3er lugar entre ocho concursantes? (Oro / Plata / Bronce)

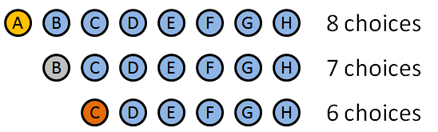
medallas de ejemplo de permuación

Vamos a usar permutaciones ya que el orden en que entregamos estas medallas importa. Así es como se desglosa:

  • Medalla de oro: 8 opciones: A B C D E F G H (Ingenioso cómo hice que los nombres coincidieran con las letras, ¿eh?). Digamos que A gana el Oro.
  • Medalla de plata: 7 opciones: B C D E F G H. Digamos que B gana la plata.
  • Medalla de bronce: 6 opciones: C D E F G H. Digamos que C C gana el bronce.

Elegimos a ciertas personas para ganar,pero los detalles no importan: al principio teníamos 8 opciones, luego 7 y luego 6. El número total de opciones fue $8 * 7 * 6 = 336$.

Veamos los detalles. Tuvimos que pedir 3 personas de 8. Para hacer esto, comenzamos con todas las opciones (8) y luego las quitamos una a la vez (7, luego 6) hasta que nos quedamos sin medallas.

sabemos que el factorial es:

\displaystyle{ 8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 }

¡Desafortunadamente, eso hace demasiado! Sólo queremos $8 * 7 * 6$. ¿Cómo podemos «detener» el factorial a las 5?

aquí es donde permutaciones enfriar: observe cómo queremos deshacernos de $5 * 4 * 3 * 2 * 1$. Cuál es otro nombre para esto? 5 factorial!

Entonces, si hacemos 8!/5! obtenemos:

\ displaystyle {\frac{8!}{5!} = \frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \cdot 6}

¿Y por qué usamos el número 5? Porque quedó después de que escogimos 3 medallas de 8. Así, una mejor manera de escribir esto sería:

\displaystyle{\frac{8!}{(8-3)!}}

donde 8!/(8-3)! es solo una forma elegante de decir » ¡Usa los primeros 3 números de 8!”. Si tenemos un total de n artículos y queremos elegir k en un orden determinado, obtenemos:

\displaystyle {\frac{n!{(n-k)!}}

Y esta es la fórmula de permutación de fantasía: Tiene n elementos y desea encontrar el número de formas en que se pueden ordenar k elementos:

\displaystyle{P (n,k) = \frac{n!{(n-k)!}}

Combinaciones, Ho!Las combinaciones

son fáciles de usar. El orden no importa. Puedes mezclarlo y se ve igual. Digamos que soy un tacaño y no puedo permitirme medallas de Oro, Plata y Bronce separadas. De hecho, solo puedo permitirme latas vacías.

¿De cuántas maneras puedo regalar 3 latas a 8 personas?

Bueno, en este caso, el orden que elegimos no importa. Si le doy una lata a Alice, Bob y luego a Charlie, es lo mismo que darle a Charlie, Alice y luego a Bob. De cualquier manera, están igualmente decepcionados.

Esto plantea un punto interesante-tenemos algunas redundancias aquí. Alice Bob Charlie = Charlie Bob Alice. Por un momento, vamos a averiguar cuántas maneras podemos reorganizar a 3 personas.

Bueno, tenemos 3 opciones para la primera persona, 2 para la segunda y solo 1 para la última. Así que tenemos $3 * 2 * 1 ways formas de reorganizar a 3 personas.

Espera un minuto this ¡esto se parece un poco a una permutación! ¡Me engañaste!

De hecho lo hice. Si tienes N personas y quieres saber cuántos arreglos hay para todos ellos, ¡es solo N factorial o N!

Así, si tenemos 3 latas para regalar, hay 3! o 6 variaciones para cada elección que elijamos. Si queremos averiguar cuántas combinaciones tenemos, simplemente creamos todas las permutaciones y dividimos por todas las redundancias. En nuestro caso, obtenemos 336 permutaciones (desde arriba), y dividimos por las 6 redundancias para cada permutación y obtenemos 336/6 = 56.

La fórmula general es

\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}

que significa » Encuentra todas las formas de elegir a k personas de n, y divídelas por k! variante”. Escribiendo esto, obtenemos nuestra fórmula de combinación, o el número de formas de combinar k elementos de un conjunto de n:

\displaystyle{C (n,k) = \frac{n!{(n-k)!¡k!}}

a Veces C(n,k) se escribe como:

\displaystyle{\binom {n}{k}}

que es el coeficiente binomial.

Algunos ejemplos

Aquí hay algunos ejemplos de combinaciones (el orden no importa) de permutaciones (el orden importa).Combinación

  • : Elegir un equipo de 3 personas de un grupo de 10. C C ( 10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.Permutación: Elegir un Presidente, Vicepresidente y Aguador de un grupo de 10. P P ( 10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • Combinación: Elegir 3 postres de un menú de 10. C (10,3) = 120.Permutación

    : Enumere sus 3 postres favoritos, en orden, de un menú de 10. P (10,3) = 720.

No memorice las fórmulas, comprenda por qué funcionan. Las combinaciones suenan más simples que las permutaciones, y lo son. Tienes menos combinaciones que permutaciones.

Otros Posts De Esta Serie

  1. Permutaciones y Combinaciones fáciles
  2. Navegar por una Cuadrícula Usando Combinaciones Y Permutaciones
  3. Cómo Entender Combinaciones Usando Multiplicación
  4. ¿Por qué multiplicamos combinaciones?