los Números Complejos: Introducción (página 1 de 3)

Secciones: Introducción, Operaciones con complejos, La Fórmula Cuadrática

hasta ahora, usted ha dicho que usted no puede tomar la raíz cuadrada de un número negativo. Esto se debe a que no tenías números que fueran negativos después de haberlos cuadrado (por lo que no podías «retroceder» tomando la raíz cuadrada). Cada número fue positivo después de que lo cuadraste. Así que no podrías muy bien poner la raíz cuadrada de un negativo y esperar que se te ocurra algo sensato.

Ahora, sin embargo, puede tomar la raíz cuadrada de un número negativo, pero implica usar un nuevo número para hacerlo. Este nuevo número fue inventado (¿descubierto? alrededor de la época de la Reforma. En ese momento, nadie creía que se encontraría ningún uso en el «mundo real» para este nuevo número, aparte de facilitar los cálculos involucrados en la resolución de ciertas ecuaciones, por lo que el nuevo número se veía como un número ficticio inventado por conveniencia.

(Pero entonces, cuando lo piensas, ¿no son todos los números inventos? ¡No es como si los números crecieran en los árboles! Viven en nuestras cabezas. Nos hizo a todos! ¿Por qué no inventar uno nuevo, siempre y cuando funcione bien con lo que ya tenemos?)

a Continuación:

Ahora, usted puede pensar que usted puede hacer esto:

Pero esto no tiene ningún sentido! Ya tienes dos números que cuadran a 1; a saber, -1 y +1. Y ya cuadradas a -1. Así que no es razonable que también cuadrara a 1. Esto señala un detalle importante: Al tratar con imaginarios, ganas algo (la capacidad de lidiar con negativos dentro de raíces cuadradas), pero también pierdes algo (algunas de las reglas flexibles y convenientes que solías tener al tratar con raíces cuadradas). En particular, ¡SIEMPRE DEBES HACER LA PARTE i PRIMERO!

• Simplificar sqrt (-9). Copyright © Elizabeth Stapel 2000-2011 Todos los derechos Reservados

(Advertencia: El paso que pasa por el tercer signo «igual» es ««, no»«. El yo está fuera de lo radical.)

• Simplificar sqrt (-25).

• Simplificar sqrt(-18).

• Simplificar –sqrt(-6).

En sus cálculos, usted tratará con i, como se haría con x, excepto por el hecho de que x2 es simplemente x2, pero i2 -1:

• Simplificar 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Simplificar 16i – 5i.

16i – 5i = (16 – 5)i = 11i

• Multiplicar y simplificar (3i)(4i).

(3i)(4i) = (3·4)(i·i) = (12)(i2) = (12)(-1) = -12

• Multiplicar y simplificar (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

tenga en cuenta a este último problema. Dentro de él, puede ver que , porque i2 = -1. Continuando, obtenemos:

Este patrón de potencias, signos, 1 e i es un ciclo:

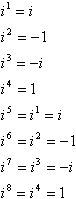
En otras palabras, para calcular cualquier potencia alta de i, puede convertirla a una potencia más baja al tomando el múltiplo más cercano de 4 que no es mayor que el exponente y restando este múltiplo del exponente. Por ejemplo, una pregunta capciosa común en las pruebas es algo parecido a» Simplificar i99″, la idea es que intentarás multiplicar i noventa y nueve veces y te quedarás sin tiempo, y los profesores se reirán a tu costa en la sala de profesores. Así es como funciona el acceso directo:

i99 = i96+3 = i(4×24)+3 = i3 = –i

Es decir, i99 = i3, porque solo puede cortar el i96. (Noventa y seis es un múltiplo de cuatro, por lo que i96 es solo 1, que puede ignorar. En otras palabras, puede dividir el exponente por 4 (usando división larga), descartar la respuesta y usar solo el resto. Esto te dará la parte del exponente que te importa. Estos son algunos ejemplos más:

• Simplify i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• Simplificar i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Simplificar i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>