Las matemáticas son más un maratón que un sprint: es un recorrido largo, lento y constante, con momentos excepcionales de avance. Aún así, de vez en cuando, obtenemos esos preciados momentos «Eureka», esas líneas cortas de letras y números que cambian la ciencia para siempre. Estas son algunas de las ecuaciones más famosas, desde los antiguos griegos hasta la física moderna.

Teorema de Pitágora (530 AC)

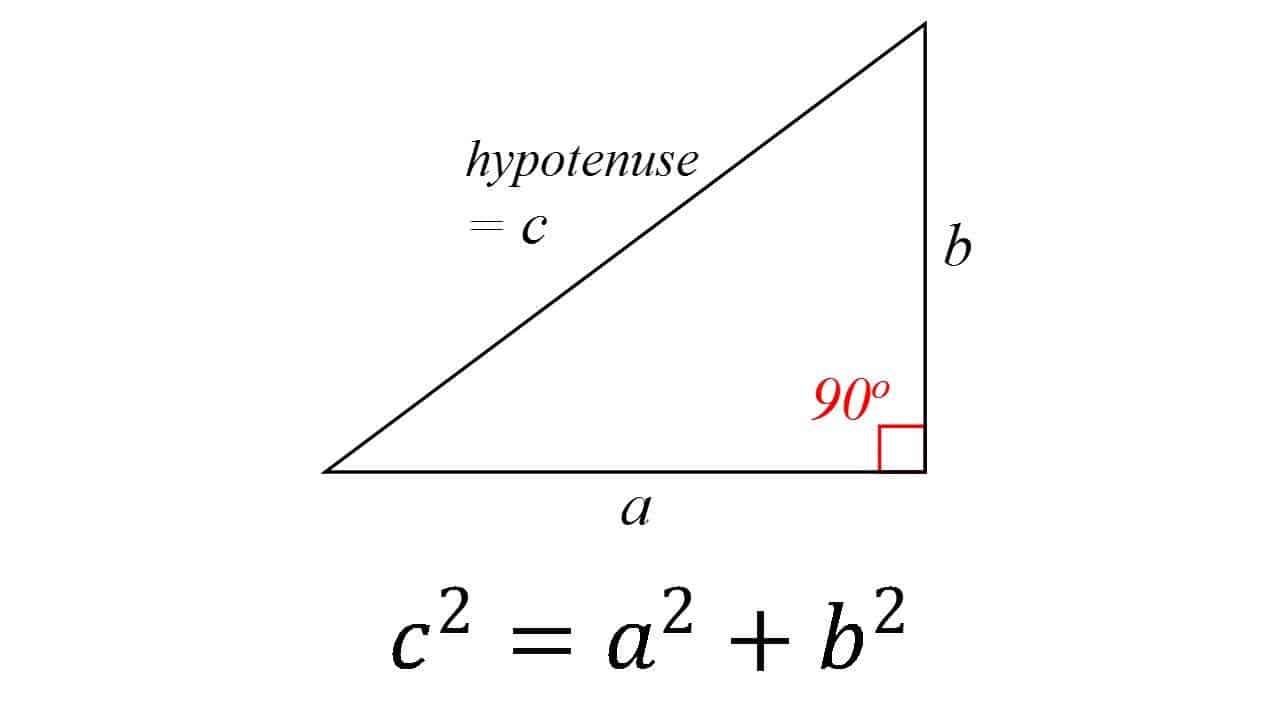
Este es uno de los pilares fundamentales de toda la geometría: en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos. La teoría se atribuye generalmente al matemático griego Pitágoras, aunque hay alguna evidencia de que los matemáticos babilónicos entendieron la fórmula. También es muy posible que el teorema fuera conocido por mucha gente, pero él fue el primero en probarlo.

El teorema ha recibido numerosas pruebas, posiblemente la mayor para cualquier teorema matemático. Son muy diversas, incluyendo tanto pruebas geométricas como pruebas algebraicas, algunas de las cuales datan de miles de años atrás.

números Complejos

El matemático italiano Gerolamo Cardano es el primero conocido en la introducción de los números complejos, llamándolos «ficticio» en el tiempo. Sin embargo, el desarrollo matemático de «i» como el número imaginario que representa la raíz cuadrada de -1 se atribuye a Leonhard Euler, uno de los matemáticos y científicos más importantes de la historia de la humanidad.

Los números complejos son básicamente números que en realidad no existen, pero que son muy útiles para varios cálculos. Consisten en números con una parte real (los números que todos conocemos) y una parte imaginaria (el que representé aquí) y tienen aplicaciones prácticas en muchos campos, incluida la física, la química, la biología, la economía, la ingeniería eléctrica y la estadística.

Los logaritmos

los Logaritmos son, básicamente, la función inversa de la exponenciación. Se necesita un número (N), una base (a), y el logaritmo de N en la base a será x, donde N es igual a a a la potencia de x. Puede parecer solo una forma diferente de escribir lo mismo (y en cierto sentido, lo es), pero los logaritmos tienen una miríada de aplicaciones prácticas, que se utilizan en psicología, economía y mediciones de muchos fenómenos físicos (como el pH o la magnitud del terremoto).

Los logaritmos fueron propuestos públicamente por John Napier en 1614, en un libro titulado Mirifici Logarithmorum Canonis Descriptio (Descripción de la Maravillosa Regla de los Logaritmos), un título apropiado. Un caso especial de logaritmo es el logaritmo natural-e, donde e es un número irracional y trascendental aproximadamente igual a 2,71828182845. De hecho, e tiene una historia fascinante y un número impresionante de aplicaciones, pero esa es una historia para otro momento.

Cálculo

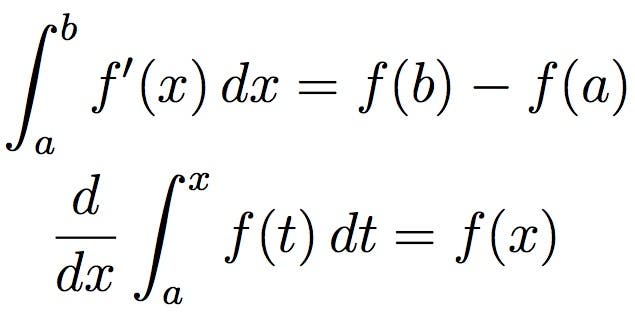
Algunos de los campos de las matemáticas han sido tan impactantes como el cálculo. Desarrollado en el siglo XVII por Isaac Newton y Gottfried Wilhelm Leibniz, el cálculo es ampliamente utilizado en ciencia, ingeniería y economía. El cálculo generalmente se enfoca en tratar con pequeñas cantidades, particularmente cantidades infinitamente pequeñas. A través del cálculo, estos pueden tratarse como números reales, a pesar de que son técnicamente infinitamente pequeños.

Para una visualización más simple, la integración, descrita anteriormente, puede considerarse como la medición del área bajo una curva, definida por una función.

La Ley de la Gravedad

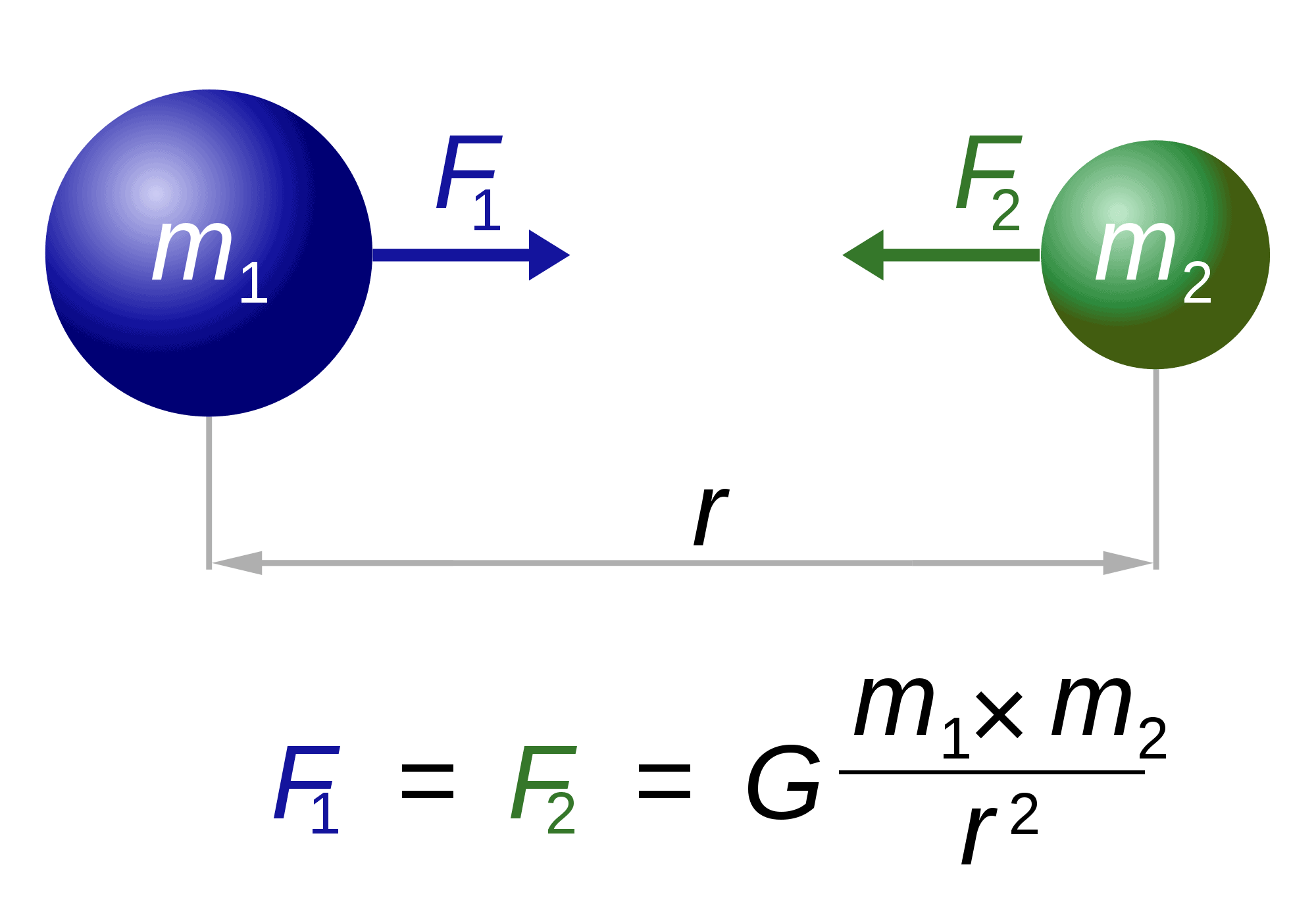
Hablando de Newton, también es «responsable» de una de las ecuaciones más famosas y espectaculares del mundo: la ley de la gravedad.

La ley básicamente describe cómo dos cuerpos de masas m1 y m2 se atraen entre sí. La fuerza (F1, F2) es inversamente proporcional al cuadrado de la distancia entre ellos (r). El único factor restante, G, es una constante gravitacional. La naturaleza de esta constante sigue siendo esquiva.

Relatividad general

Durante casi 200 años, la ley de Newton definió nuestro nivel de comprensión de la mecánica. El trabajo de Einstein en el siglo XX llevó las cosas al siguiente nivel: estos dos logros se elevan en los pedestales más altos del mundo de la física.

La relatividad general es esencialmente una teoría geométrica de la gravitación, generalizando la teoría de Newton proporcionando una descripción unificada de la gravedad como una propiedad geométrica del espacio y el tiempo, o espacio — tiempo. En particular, Einstein demostró no solo que existe tal cosa como» espacio-tiempo » que fusiona las tres dimensiones con la cuarta dimensión del tiempo, sino que también demostró que este espacio-tiempo puede curvarse por gravedad, con la curvatura directamente relacionada con la energía y el momento de cualquier materia y radiación presentes.

Segunda ley de la termodinámica

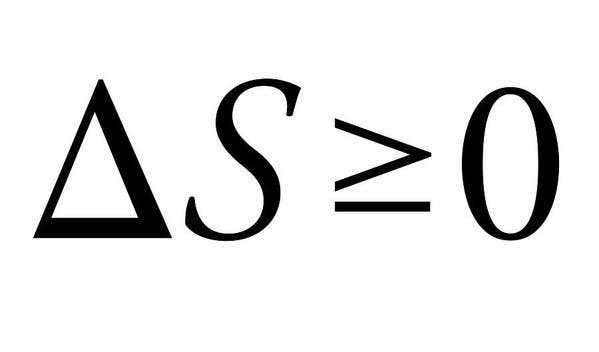
La Segunda Ley de la Termodinámica es por qué no podemos tener cosas buenas en el Universo. Bromas aparte, las cuatro leyes de la termodinámica definen cantidades físicas fundamentales (temperatura, energía y entropía) que caracterizan a los sistemas termodinámicos. El segundo, en particular, destaca aquí por su simplicidad, pero con implicaciones absolutamente masivas.

La ley establece esencialmente que la suma de las entropías de los sistemas termodinámicos que interactúan siempre debe aumentar, o a lo sumo permanecer constante. Cuando la energía cambia de una forma a otra o la materia se mueve, la entropía (o desorden) en un sistema cerrado aumenta. Todas las diferencias en temperatura, presión y densidad tienden a aplanarse después de un tiempo

Las ecuaciones de Maxwell

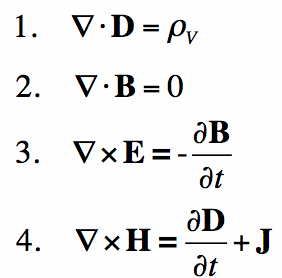
En pocas palabras, las ecuaciones de Maxwell son para el electromagnetismo lo que la ley de Newton es para la mecánica. Proporcionan una base matemática para el electromagnetismo clásico, la óptica clásica y los circuitos eléctricos. Son ampliamente utilizados en el mismo dispositivo en el que está leyendo esto, básicamente, en todos los dispositivos electrónicos.

Las leyes de Maxwell describen cómo los campos eléctricos y magnéticos son generados por cargas, corrientes y cambios de los campos. Un avance significativo fue la demostración de que los campos eléctricos y magnéticos se propagan a la velocidad de la luz.

Identidad de Euler

Por último, esta es posiblemente la ecuación más elegante, una cosa de belleza suprema, porque involucra todos los números «básicos»:

• 0, que es neutral para la suma y la resta;
• 1, que es neutral para la multiplicación y la división;
• e, que es el número de Euler (ver arriba), la base de logaritmos naturales;
• i es la unidad imaginaria (ver arriba); y
• π es pi, la relación entre la circunferencia de un círculo y su diámetro.

Encontrar una relación que unifique todos estos números es nada menos que impresionante, y parece bastante improbable. La demostración no es exactamente simple, pero se puede ver aquí.

Es lógico que el profesor de matemáticas de la Universidad de Stanford Keith Devlin describiera la ecuación, diciendo que «al igual que un soneto shakesperiano que captura la esencia misma del amor, o una pintura que resalta la belleza de la forma humana que es mucho más que superficial, la ecuación de Euler llega hasta las profundidades de la existencia»

No es frecuente que las matemáticas y la física se reduzcan a ecuaciones simples y elegantes, pero cuando lo hacen, es todo un espectáculo para la vista.