Evaluación de Kappa de Cohen

El valor de kappa puede ser inferior a 0 (negativo). Una puntuación de 0 significa que hay acuerdo aleatorio entre los evaluadores, mientras que una puntuación de 1 significa que hay un acuerdo completo entre los evaluadores. Por lo tanto, una puntuación que es menor que 0 significa que hay menos concordancia que la probabilidad aleatoria. A continuación, le mostraré la fórmula para resolver esto, pero es importante que se familiarice con la figura 4 para tener una comprensión sólida.

la razón por La que destacaron dos redes se pondrá de manifiesto en un momento, pero por ahora, permítanme romper cada cuadrícula.

A => El número total de instancias que ambos evaluadores dijeron que eran correctas. Los evaluadores están de acuerdo.

B => El número total de instancias que el Evaluador 2 dijo que eran incorrectas, pero el Evaluador 1 dijo que eran correctas. Esto es un desacuerdo.

C => El número total de instancias que el Evaluador 1 dijo que eran incorrectas, pero el Evaluador 2 dijo que eran correctas. Esto también es un desacuerdo.

D => El número total de instancias que ambos evaluadores dijeron que eran incorrectas. Los evaluadores están de acuerdo.

Para calcular el valor kappa, primero necesitamos saber la probabilidad de concordancia (esto explica por qué resalté la diagonal de concordancia). Esta fórmula se obtiene sumando el número de pruebas en las que los evaluadores están de acuerdo y luego dividiéndola por el número total de pruebas. Usando el ejemplo de la figura 4, eso significaría (A + D)/(A + B+ C+ D).

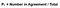
Perfecto! El siguiente paso es calcular la probabilidad de acuerdo aleatorio. Usando la figura 4 como guía, el valor esperado es el número total de veces que el Evaluador 1 dijo correcto dividido por el número total de instancias, multiplicado por el número total de veces que el Evaluador 2 dijo correcto dividido por el número total de instancias, agregado al número total de veces que el Evaluador 1 dijo incorrecto multiplicado por el número total de veces que el Evaluador 2 dijo incorrecto. Es mucha información para asimilar, así que en la figura 6 he formulado esta ecuación usando la cuadrícula de arriba.

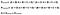
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

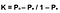
Genial! Ahora puede distinguir entre fiabilidad y validez, explicar el kappa de Cohen y evaluarlo. Esta estadística es muy útil, aunque ya que he entendido cómo funciona, ahora creo que puede estar infrautilizada al optimizar algoritmos a una métrica específica. Además, el kappa de Cohen también hace un buen trabajo al medir problemas de clases múltiples y desequilibradas.

P.D. Si hay algo que quieres que cubra que tenga que ver con la ciencia de datos, puedes enviarme un mensaje directo en Twitter @KurtisPykes o dejar una respuesta a este post.