Integrales definidas
¡Le gustaría leer Introducción a la Integración primero!
Integración
|
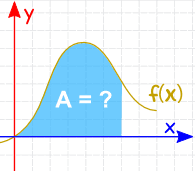
La integración se puede utilizar para encontrar áreas, volúmenes, puntos centrales y muchas cosas útiles. Pero a menudo se usa para encontrar el área debajo del gráfico de una función como esta: |
 |
||
|
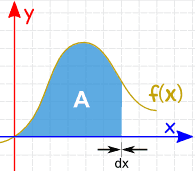
El área se puede encontrar agregando segmentos que se acercan a cero en ancho: Y hay Reglas de Integración que nos ayudan a obtener la respuesta. |
 |
Notación
El símbolo para «Integral» es una elegante «S» (para «Suma», la idea de sumar segmentos):
Después del Símbolo Integral ponemos la función de la que queremos encontrar la integral (llamada el Integrador).
Y luego termina con dx para significar que los cortes van en la dirección x (y se acercan a cero en ancho).
Integral definida
Una Integral Definida tiene valores iniciales y finales: en otras palabras, hay un intervalo .
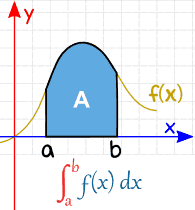
a y b (llamados límites, límites o límites) se colocan en la parte inferior y superior de la «S», así:
 |
 |
|
| Definite Integral (from a to b) |
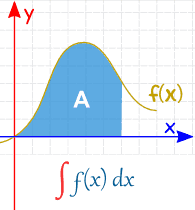
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
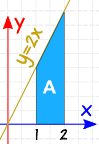
Ejemplo: Qué es 2 ∫ 1 2x dx
Se nos pide la Integral Definida, de 1 a 2, de 2x dx
Primero necesitamos encontrar la Integral Indefinida Integral.
el Uso de las Reglas de Integración, nos encontramos con que ∫2x dx = x2 + C
Ahora se calcula que en 1 y 2:
- En x=1: ∫2x dx = 12 + C
- En x=2: ∫2x dx = 22 + C
Restar:
Y «C» se cancela … así que con las Integrales Definidas podemos ignorar C.
Resultado:

de Verificación: con tal de una forma simple, también vamos a tratar de calcular el área de la geometría:
Un = 2+42 × 1 = 3
Sí, tiene un área de 3.
(Yay!Notación
: Podemos mostrar la integral indefinida (sin el +C) dentro de los corchetes, con los límites a y b después de que, como este:
Ejemplo (continuación)
Una buena manera de mostrar su respuesta:
=
intentemos otro ejemplo:
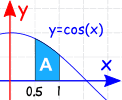
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
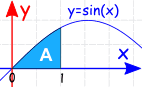
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
La Integral Indefinida es: ∫sin(x) dx = −cos(x) + C
Puesto que se va de 0, ¿se puede calcular la integral en x=1?
− – cos ( 1) = -0,540…
¿Qué? Es negativo? Pero parece positivo en el gráfico.
Bien … ¡cometimos un error!
Porque necesitamos restar la integral en x = 0. No debemos asumir que es cero.
Así que hagámoslo correctamente, restando una de la otra:
=
¡Eso es mejor!
Pero podemos tener regiones negativas, cuando la curva está por debajo del eje:
Ejemplo:
La Integral Definida, de 1 a 3, de cos(x) dx:
Observe que algunos son positivos y otros negativos.
La integral definida calculará el valor neto.
Déjanos hacer los cálculos:
=
hay más negativo que positivo con el resultado neto de -0.700….
así que tenemos esta cosa importante que recordar:
Intente integrar cos(x) con diferentes valores de inicio y final para ver por sí mismo cómo funcionan los positivos y los negativos.
Área positiva
Pero a veces queremos que toda el área se trate como positiva (sin restar la parte debajo del eje).
En ese caso debemos calcular las áreas por separado, como en este ejemplo:

Ejemplo: ¿Cuál es el área total entre y = cos (x) y el eje x, de x = 1 a x = 3?
Esto es como el ejemplo que acabamos de hacer, pero ahora esperamos que toda el área sea positiva (imagina que tuviéramos que pintarla).
Así que ahora tenemos que hacer las piezas por separado:
- Uno para el área sobre el eje de las x
- Uno para el área por debajo del eje x
La curva cruza el eje x en x = π/2 por lo tanto tenemos:
De 1 a π/2:
= sen(π/2) − sin(1)
Desde π/2 a 3:
= sin(3) − sen(π/2)
la última sale negativo, pero queremos que sea positivo, así:
área Total = 0.159… + 0.859… = 1.018…
Esto es muy diferente de la respuesta del ejemplo anterior.
Continuo
Oh sí, la función que estamos integrando debe ser Continua entre a y b: sin agujeros, saltos o asíntotas verticales (donde la función se dirige hacia arriba/abajo hacia el infinito).
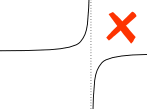
Ejemplo:
Una asíntota vertical entre a y b afecta a la integral definida.
Propiedades
Área por encima-área por debajo
La integral suma el área por encima del eje pero resta el área por debajo, para un «valor neto»:
Agregar funciones
La integral de f+g es igual a la integral de f más la integral de g:
Revertir el intervalo
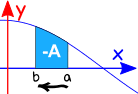
la inversión de la dirección de intervalo se le da a la negativa de la dirección original.
![]()


Leave a Reply