Entendiendo Fracciones Equivalentes

Las fracciones equivalentes representan la misma parte de un todo

La mejor manera de pensar en fracciones equivalentes es que son fracciones que tienen el mismo valor general.

Por ejemplo, si cortamos un pastel exactamente por el centro, en dos piezas del mismo tamaño, una pieza es igual a la mitad del pastel.

Y si se corta otro pastel (del mismo tamaño) en 4 piezas iguales, dos piezas de ese pastel representan la misma cantidad de pastel que 1/2.

Así que podemos decir que 1/2 es equivalente (o igual) a 2/4.

¡No dejes que las fracciones equivalentes te confundan!

Eche un vistazo a los cuatro círculos de arriba.¿Puedes ver que el «1/2″, los dos» 1/4 «y los cuatro» 1/8 » ocupan la misma cantidad de área coloreada en naranja para su círculo?Bueno, eso significa que cada área coloreada en naranja es una fracción equivalente o una cantidad igual. Por lo tanto, podemos decir que 1/2 es igual a 2/4, y 1/2 también es igual a 4/8. Y sí, saltamontes, 2/4 es una fracción equivalente a 4/8 too.As ya lo sabes, estamos locos por las reglas. Por lo tanto, echemos un vistazo a la Regla para comprobar si dos fracciones son equivalentes o iguales. La regla para fracciones equivalentes puede ser un poco difícil de explicar, pero aguanta, aclararemos las cosas en un poco.

he Aquí la Regla

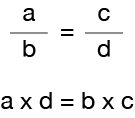
Lo que esta Regla dice es que dos fracciones son equivalentes (iguales) sólo si el producto del numerador (a) de la primera fracción y el denominador (d) de la otra fracción es igual al producto del denominador (b) de la primera fracción y el numerador (c) de la otra fracción.

Un producto simplemente significa que multiplicas.

Eso suena como un trabalenguas, así que intentémoslo con números

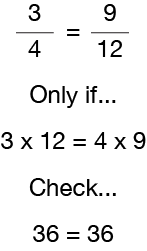
Probar la Regla

Ahora conectemos los números a la Regla de fracciones equivalentes para asegurarnos de que la tiene «fría». 3/4 son equivalentes (iguales) 9/12 sólo si el producto del numerador (3) de la primera fracción y el denominador (12) de la otra fracción es igual al producto del denominador (4) de la primera fracción y el numerador (9) de la otra fracción. Así que sabemos que 3/4 es equivalente a 9/12, porque 3×12 = 36 y 4×9 = 36. Una forma sencilla de ver cómo verificar fracciones equivalentes es hacer lo que se llama «multiplicación cruzada», que significa multiplicar el numerador de una fracción por el denominador de la otra fracción. Luego haz lo mismo al revés. Ahora compare las dos respuestas para ver si son iguales. Si son iguales, entonces las dos fracciones son fracciones equivalentes.

El siguiente gráfico le muestra cómo multiplicar por cruz

Bien, hagamos uno con números donde las fracciones no son equivalentes

Como puede ver en este ejemplo, 1/2 no es una fracción equivalente de 2/3.

Si recuerda utilizar el método de multiplicación cruzada, no debería tener problemas para verificar fracciones equivalentes.

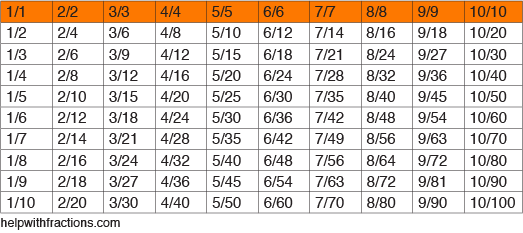
La siguiente tabla enumera algunas fracciones comunes y sus equivalentes. Lee la mesa de izquierda a derecha. Lo que muestra son valores multiplicados por diferentes variaciones de fracciones iguales a»1″. ¿Recuerdas que cualquier número dividido por sí mismo es igual a» 1″, verdad?