Con el éxito de taquilla de la película «Interestelar», muchas personas están entusiasmadas con las perspectivas de los agujeros de gusano como un medio para el transporte interestelar. Aunque actualmente no hay evidencia de que tales objetos exóticos existan en la naturaleza, es posible que pudieran ser creados artificialmente, tal vez a partir de versiones de la teoría de cuerdas de dimensiones superiores e ingeniería de la espuma espacio-temporal fundamental. La investigación de agujeros de gusano es hoy un tema emocionante con docenas de artículos publicados en revistas revisadas por pares cada año, pero vale la pena recordar sus orígenes, y comienza en un lugar sorprendente.

En 1915 Albert Einstein publicó su teoría general de la relatividad, su descripción de la gravedad que define claramente cómo los objetos se atraerán entre sí y afectarán el espacio y el tiempo que los rodea. Muchos años más tarde, el físico estadounidense John Wheeler acuñaría la frase «el espacio le dice a la materia cómo moverse, y la materia le dice al espacio cómo curvarse». Einstein describió la gravedad como una manifestación de la curvatura espacio-temporal. La relatividad General es una teoría de campos continuos en contraste con la teoría de partículas de la materia que condujo a la mecánica cuántica.

Einstein también participó en el desarrollo de la mecánica cuántica, la teoría que describe las partículas subatómicas. Pero no estaba del todo contento con sus incertidumbres inherentes y su carácter probabilístico. En 1935, trabajó con Nathan Rosen para producir una teoría de campos para electrones, usando la relatividad general. Su artículo se tituló «El Problema de las Partículas en la Teoría General de la Relatividad». Einstein y Rosen estaban investigando la posibilidad de una teoría atomística de la materia y la electricidad que, excluyendo discontinuidades (singularidades) en el campo, no hizo uso de otras variables que la descripción (métrica) de la relatividad general y la teoría electromagnética de Maxwell. Una de las consecuencias fue que se encontró que la partícula cargada más elemental era una de masa cero.

Al final, lo que produjeron fue algo bastante original. Comenzaron con las ecuaciones para una distribución de masa esférica simétrica, ya utilizada para agujeros negros, y conocida como la solución de Schwarzschild,

ds ds^2 = -\dfrac{1}{1-2m/r}dr^2 – r^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)dt^2

donde \(ds^2\) es la métrica y \(m=GM/c^2\) con coordenadas esféricas \((r,\theta,\phi)\) y tiempo \(t\).

Realizaron una transformación de coordenadas para eliminar la región que contiene la singularidad de curvatura, una discontinuidad en la curvatura del espacio implicada por agujeros negros y fenómenos similares. La singularidad en \(r=2m\) fue eliminado por la transformación de coordenadas \(u^2 = r – 2m\), resultando en una solución final,

$$ds^2 = -4(u^2 + 2m)du^2 – (u^2 + 2m)^2 d\Omega^2 + \dfrac{u^2}{u^2 + 2m} dt^2$$

donde \(d\Omega^2 = d\theta^2 + \sin^2\theta d\phi^2\).

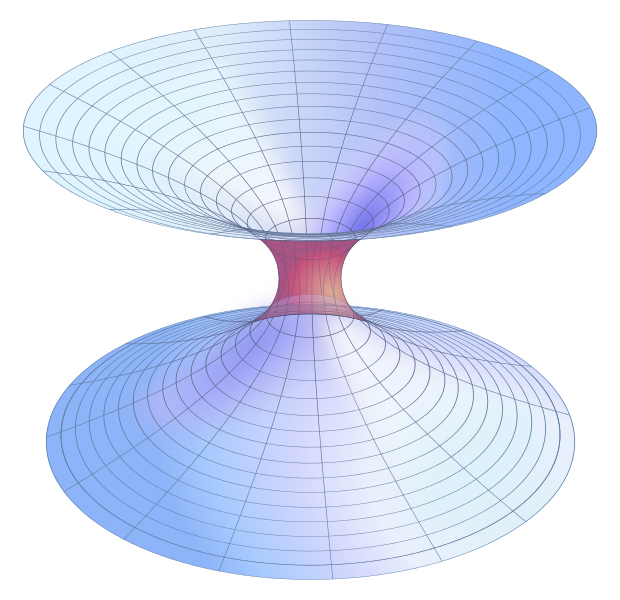
Esta solución era una representación matemática del espacio físico por un espacio de dos hojas asintóticamente planas conectadas por un puente o un agujero de gusano Schwarzschild con una «garganta». Esto conecta las dos hojas y, por analogía, dos partes separadas del universo real tridimensional. La Figura 1 muestra el espacio alrededor del agujero de gusano, con el espacio arriba y abajo haciéndose plano en los «bordes» a medida que se aleja hacia el infinito.

Este no era un agujero de gusano atravesable, para eso tuvimos que esperar la llegada de los físicos John Wheeler en la década de 1950 y Kip Thorne en la década de 1980. En 1987, con el apoyo de Carl Sagan para su novela «Contact» (más tarde un largometraje), Thorne y su colega Michael Morris fueron capaces de construir una descripción matemática, una métrica, para describir un agujero de gusano esférico simétrico y estático con una circunferencia real finita. Esto tenía una disminución coordinada de infinito negativo en el espacio mínimamente curvo, a un valor mínimo donde se encontraba la garganta, y luego aumentaba desde la garganta hasta el infinito positivo, en un espacio mínimamente curvo diferente. Esta solución tiene la característica distintiva de no tener horizonte de eventos, a diferencia de un agujero negro. El artículo de Thorne y Morris se tituló «Agujeros de gusano en el Espacio-tiempo y su uso para Viajes Interestelares: Una Herramienta para Enseñar la Relatividad General». Este artículo ayudó a establecer la investigación de agujeros de gusano como una nueva área de investigación académica.

Desde entonces, se han publicado muchos artículos, y de hecho se han realizado estudios astronómicos, examinando las estrellas y galaxias más lejanas en busca de agujeros de gusano naturales. Todavía no se ha identificado ninguno, pero recuerde el origen de este campo de investigación: el Puente Einstein — Rosen no era un agujero de gusano atravesable, y no era la intención del autor producir uno, pero sí produjeron la primera descripción matemática de un agujero de gusano. Deberían ser recordados por esto. La investigación científica a menudo produce algo bastante inesperado con implicaciones que van mucho más allá de las intenciones originales de los investigadores.

Kelvin F. Desde que se publicó este artículo, nuestra revista, Principium, ha publicado dos números (números 9 & 10) donde discutimos los agujeros de gusano y el Puente Einstein-Rosen con más detalle. Estos temas también detallan el simposio de un día sobre «Agujeros de gusano Interestelares: Física y Realización Práctica» organizado por la Iniciativa para Estudios Interestelares en colaboración con la Sociedad Interplanetaria Británica.