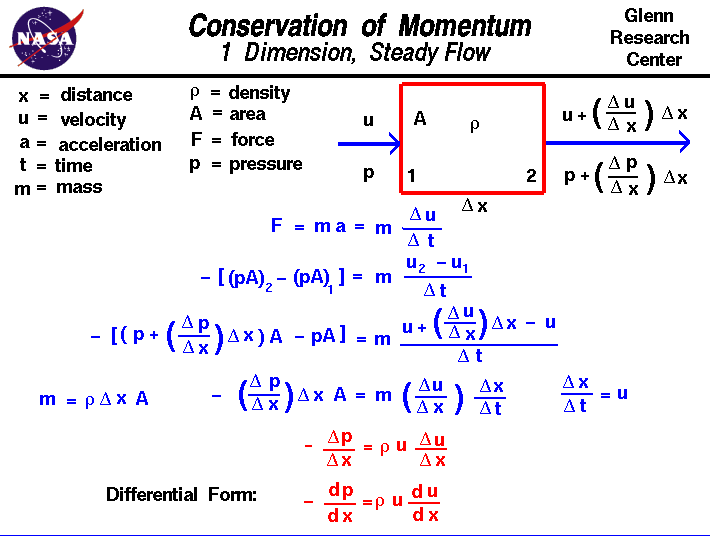
La conservación del momento es un concepto fundamental de lo físico junto con la conservación de la energía y la conservación de la masa.El momento se define como la masa de un objeto multiplicada por la velocidad del objeto.La conservación del impulso indica que, dentro de algún dominio del problema, la cantidad de impulso permanece constante;el impulso no se crea ni se destruye, sino que solo se cambia a través de la acción de las fuerzas como se describe en las garras del movimiento de Newton.Lidiar con el momento es más difícil que lidiar con la masa y la energía porque el momento es una cantidad de un sector que tiene una magnitud y una dirección. El momento se conserva en las tres direcciones físicas al mismo tiempo. Es aún más difícil cuando se trata de agas, ya que las fuerzas en una dirección pueden afectar el momento en otra dirección debido a las colisiones de muchas moléculas.En esta diapositiva, presentaremos un problema de flujo muy, muy simplificado donde las propiedades solo cambian en una dirección.El problema se simplifica aún más al considerar un flujo constante que no cambia con el tiempo y al limitar las fuerzas solo a aquellas asociadas con thepressure.Be consciente de que los problemas de flujo reales son mucho más complejos que este ejemplo sencillo.

Consideremos el flujo de un gas a través de un dominio en el que las propiedades de flujo solo cambian en una dirección, que llamaremos «x». El gas entra en el dominio en la estación 1 con un poco de velocidad u y un poco de presión p y sale en la estación 2 con un valor diferente de velocidad y presión. Para simplificar, asumiremos que la densidad r permanece constante dentro del dominio y que el área A a través de la cual fluye el gas también permanece constante. La ubicación de las estaciones 1 y 2 están separadas por una distancia llamada del x. (Delta es el pequeño triángulo en el deslizamiento y es la letra griega «d». Los matemáticos a menudo usan este símbolo para denotar un cambio o variación de una cantidad. La fuente de impresión web no admite las letras griegas, por lo que simplemente la llamaremos «del».) Un cambio con la distancia se denomina gradiente para evitar confusiones con un cambio con el tiempo que se denomina tasa.El gradiente de velocidad se indica por del u / del x; el cambio en la velocidad por cambio en la distancia. Así que en la estación 2, la velocidad viene dada por la velocidad en 1 más el gradiente por la distancia.

Una expresión similar da la pressureat la salida:

la segunda ley de movimiento de Newton establece que la fuerza F es igual al cambio en el momento con respecto al tiempo. Para un objeto con masa constantem, esto se reduce a la aceleración de los tiempos de masa a.An la aceleración es un cambio en la velocidad con un cambio en el tiempo (del u / del t). Entonces:

La fuerza en este problemcomes de la gradiente de presión. Dado que la presión es una fuerza por unidad de área,la fuerza neta en nuestro dominio de fluido es la presión por el área en el exterior menos la presión por el área en la entrada.

El signo menos al principio de esta expresión se usa porque los gases se mueven de una región de alta presión a una región de baja presión; si la presión aumenta con x, la velocidad disminuirá. La sustitución de nuestras expresiones para velocityand presión:

Simplificar:

Observando que (del x / del t) es thevelocity y de que la masa es la densidad r veces el volumen (área de veces del x):

Simplificar:

El del p / del x y del u / del xrepresent la presión y los gradientes de velocidad.Si reducimos nuestro dominio a tamaños diferenciales, estos degradados se convierten en diferenciales:

Esta es una forma unidimensional y constante de Equation.It es interesante observar que la caída de presión de un fluido (el término de la izquierda) es proporcional tanto al valor de la velocidad como al gradiente de la velocidad.Una solución de esta ecuación de momento nos da la forma de la presión dinámica que aparece en la ecuación de Bernoulli.

Actividades:
Visitas guiadas

• Ecuaciones Básicas de Dinámica de Fluidos:

Navegación..

Página de Inicio de la Guía para Principiantes