Por Jason McCormick
Profesor asociado, Civil & Ingeniería ambiental, Universidad de Michigan, Ann Arbor, MI, EE.UU.

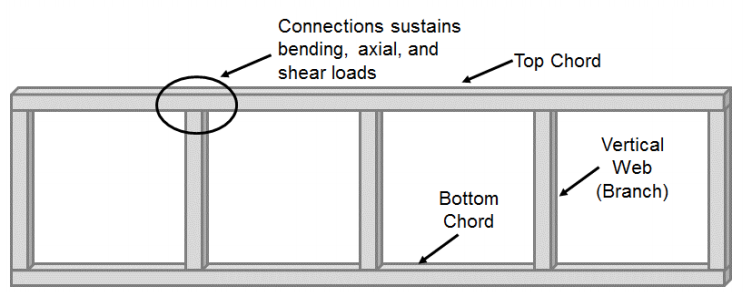
Las conexiones de momento hechas de secciones estructurales huecas rectangulares y cuadradas (HSS) han recibido menos consideración en comparación con las conexiones de HSS a HSS compuestas de miembros con carga axial (T, Y,-conexiones). La mayoría de los estudios estáticos centrados en estas conexiones han considerado sistemas de armadura Vierendeel. Estos sistemas a menudo están formados por acordes superiores e inferiores cuadrados o rectangulares que están conectados con miembros de banda vertical (rama) cuadrados o rectangulares (Figura 1). Como resultado de esta configuración, la conexión de cuerda a banda sufre una flexión significativa junto con cargas axiales y de corte y no se considera una conexión fija como se hace comúnmente en los sistemas de armadura típicos. Originalmente concebido en 1896 por Arthur Vierendeel, no fue hasta que se desarrollaron los HSS que el potencial de las vigas Vierendeel comenzó a realizarse (Korol et al. 1977), pero su uso requería una comprensión de cómo transferir momentos entre conexiones T de HSS a HSS.

Muchos de los primeros estudios de estas conexiones se centraron en la capacidad de la conexión para desarrollar la capacidad de momento completo del miembro de rama. Jubb y Redwood (1966) demostraron que cuando la sección de ramificación tenía un ancho igual al de la sección de cuerda (β=1), la capacidad de momento total del miembro HSS se podía lograr sin refuerzo. Sin embargo, este estudio no consideró la pérdida potencial de capacidad de momento debido a la presencia de carga axial. Por otro lado, Korol et al. (1977) mostraron que las conexiones con un ancho de rama más pequeño que el acorde no podían desarrollar la capacidad de momento completo de la rama sin refuerzo a través de una serie de 29 pruebas de conexión diferentes considerando 5 configuraciones diferentes (sin refuerzo, placas de refuerzo de brida de rama, refuerzos de brida de acorde, anilla y pirámide truncada). En general, la resistencia y rigidez de las conexiones de tipo Vierendeel no reforzadas disminuye con un aumento en la relación de esbeltez de los acordes (B/t) y una disminución en la relación de ancho de rama a acorde (β). Como resultado, las conexiones de tipo armadura Vierendeel no estiradas solo se pueden considerar rígidas (es decir, se someten a una rotación relativa mínima entre el acorde y la rama) cuando la relación de ancho de rama a acorde es 1.0 y la relación de esbeltez del acorde es baja o la conexión está reforzada (Packer 1993).

Debido a que los momentos máximos en estas articulaciones pueden ocurrir en deformaciones excesivamente grandes, se adopta un enfoque similar al utilizado para juntas HSS cuadradas y rectangulares con carga axial, donde se utiliza una capacidad de carga última o un límite de deformación o rotación para caracterizar el momento de diseño (Wardenier 1982). AISC 360-10 (Capítulo K3) considera tres estados límite para conexiones en T HSS cuadradas y rectangulares bajo flexión estática en el plano: plastificación de la pared de cuerdas, flanco local y flanco local de la rama debido a la distribución desigual de la carga. La plastificación de la pared de acordes se produce como resultado de que el ancho del miembro de la rama es menor que el ancho del acorde (β ≤ 0,85), lo que requiere que las cargas de tensión y compresión producidas por el momento de flexión se transfieran a través de la cara relativamente flexible del acorde en lugar de directamente a las paredes laterales más rígidas. La ecuación del estado límite (Ecuación AISC 360-10 K3-6) se puede derivar de la teoría de la línea de rendimiento (Figura 2):

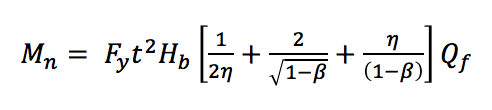
Mn es la capacidad de momento nominal de la conexión, Fy es el límite elástico mínimo especificado del acorde, Hb es la altura total de la rama, h es el parámetro de longitud de carga igual a la altura de la rama dividida por el ancho del acorde (suponiendo un ángulo de 90o entre el acorde y el miembro de la rama, como es típico de Vierendeel trusses), y Qf es un parámetro para reducir la capacidad de la unión en presencia de compresión axial en la cuerda.

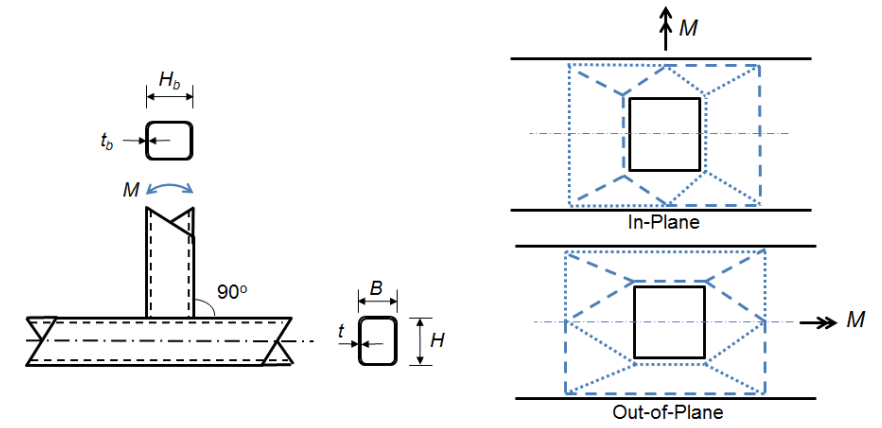
Los otros dos estados límite están asociados con conexiones donde el ancho del miembro de rama es igual o casi igual al ancho del acorde (β > 0.85), lo que significa que las cargas de tensión y compresión desarrolladas en las bridas del miembro de la rama se transfieren casi directamente a las paredes laterales más rígidas de la cuerda. El estado límite para el rendimiento local de la pared lateral (Ecuación AISC 360-10 K3-7) de una conexión en T puede derivarse de la ecuación de rendimiento local de banda para fuerzas concentradas aplicadas a una distancia desde el extremo de la barra mayor que su profundidad (Ecuación AISC 360-10 J10-2):

Mn = 0.5Fyt(Hb + 5t)2
Ecuación 2

Para el rendimiento local de la rama debido a la distribución desigual de la carga (Ecuación AISC 360-10 K3-8) en una conexión en T, se utiliza un enfoque de ancho efectivo para reducir la capacidad del elemento de refuerzo para obtener el momento nominal aplicado por el refuerzo:

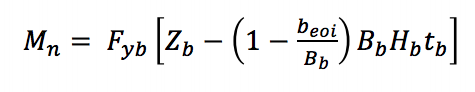
Fyb es el límite elástico mínimo especificado de la rama, Zb es el módulo de sección de plástico de la rama sobre el eje de flexión, beoi es el ancho efectivo de la rama, Bb es el ancho total de la rama y tb es el grosor de pared de diseño de la rama.

Debido a que existe evidencia experimental limitada para apoyar modelos de diseño específicos para conexiones de armadura Vierendeel (conexiones en T) bajo plegado fuera del plano, se utilizan estados límite análogos a los de plegado en el plano (Packer et al. 2010). Un estado límite adicional de falla de distorsión de acorde se desarrolla a partir del par aplicado al acorde por el miembro de rama como resultado del momento fuera del plano. Este par puede provocar una distorsión romboidal del acorde. Las ecuaciones de momento nominal para flexión fuera del plano se pueden encontrar en las ecuaciones AISC 360-10 K3-9, K3-10, K3-11 y K3-12. Las ecuaciones para la flexión tanto en el plano como fuera del plano de las conexiones en T son similares a las que se han adoptado internacionalmente (Packer et al. 2010).

Las ecuaciones de diseño anteriores se derivaron considerando los sistemas de armadura Vierendeel bajo cargas estáticas. Un estudio reciente (Fadden et al. 2015) ha promovido este trabajo para considerar el comportamiento de las conexiones de momento HSS a HSS cuadradas y rectangulares bajo grandes cargas cíclicas para su uso en sistemas de marcos de momento sísmicos basados en tubos (marcos de momento intermedios y especiales). Este sistema busca aprovechar las excelentes propiedades axiales, de flexión y de torsión, la alta relación resistencia-peso y la naturaleza arquitectónicamente agradable del HSS cuadrado y rectangular. La alta resistencia a la torsión puede conducir a una reducción en el arriostramiento lateral del haz, mientras que la alta relación resistencia-peso da como resultado una masa sísmica más baja. Sin embargo, tales conexiones deben poder someterse a un bisagra de plástico estable del miembro de la viga, donde el 80% de la capacidad de plástico del miembro de la viga se mantiene a 0,2 rad. (IMF) o 0,4 rad. (SMF) de deriva entre pisos (AISC 341-10). Dado que el diseño sísmico actual de los sistemas de marco de momentos requiere que la mayoría del comportamiento inelástico ocurra en el miembro de la viga, el miembro de la viga también debe alcanzar su capacidad plástica completa antes de someterse a pandeo local. Fadden y McCormick (2014a) consideraron tanto modelos experimentales como de elementos finitos para determinar los requisitos de ancho-espesor y espesor de profundidad límite para HSS en flexión, ya que los especificados en las Disposiciones sísmicas actuales de AISC (AISC 341-10) se desarrollaron en gran medida sobre la base de pruebas de miembros de HSS con carga axial cíclica.

Para determinar la configuración adecuada y los requisitos detallados para satisfacer esta demanda de resistencia y ductilidad, se probaron experimentalmente cuatro configuraciones de conexión diferentes: dos conexiones no reforzadas soldadas directamente (no compatibles y compatibles) y dos conexiones reforzadas (placa pasante y placa de diafragma externa). Todas las conexiones utilizaban una columna HSS de 10x10x5/8. Las conexiones soldadas directamente utilizaron soldaduras CJP precalificadas como se especifica en AWS D1.1 (2010). Para la conexión inigualable, el haz era un HSS 12x8x3/8 (β = 0.8) sugiriendo que la plastificación de la cara de la columna puede ser una preocupación. Para la conexión emparejada, la viga era un HSS 12x10x3/8 (β = 1.0) que permitía transferir las cargas directamente a la pared lateral. Se utilizó el protocolo de carga AISC para precalificación de conexiones de momento sísmico (AISC 341-10) para cargar las conexiones. El comportamiento de las conexiones fue el previsto con la conexión sin igual que mostraba deformación en la cara de la columna, mientras que la conexión emparejada era capaz de transferir la carga a las paredes laterales de la columna. Sin embargo, ambas conexiones fallaron debido a una fractura en el metal base de la columna en la punta de la esquina de la soldadura (Figura 3). Este fallo frágil a rotaciones de 0,4 rad. y 0.5 rad., respectivamente, confirmó que las conexiones soldadas directamente no proporcionan el comportamiento adecuado para aplicaciones sísmicas.

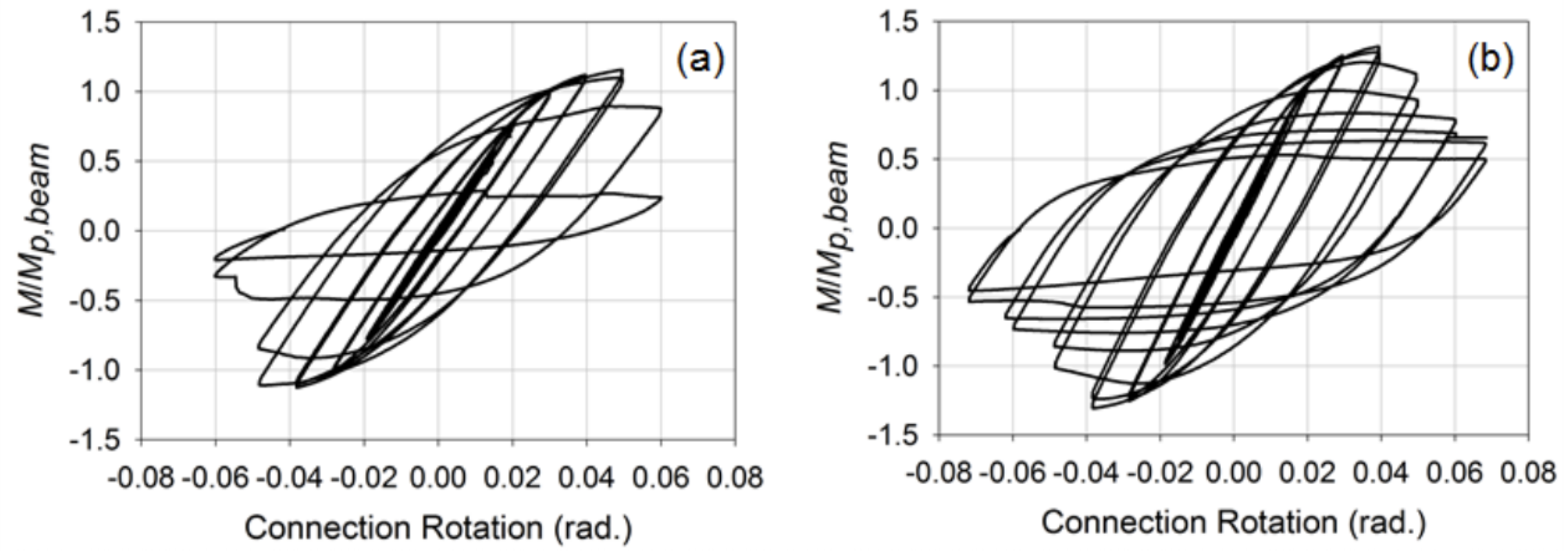
Las conexiones reforzadas se desarrollaron teniendo en cuenta las placas a través de la placa y las placas de diafragma externas que se usan a menudo en conexiones de columna de viga a HSS de brida ancha para proporcionar un mejor mecanismo para transferir las fuerzas de tensión y compresión a la pared lateral de la columna y minimizar las concentraciones de tensión colocadas en las soldaduras. Para estas conexiones, las vigas eran barras HSS 12x8x3/8 (β = 0,8). La información con respecto al procedimiento específico utilizado para diseñar y detallar estas conexiones se puede encontrar en Fadden y McCormick (2014b) y Fadden et al. (2015). Colocadas bajo la misma carga que las conexiones no reforzadas, las conexiones mostraron un comportamiento más estable con la bisagra de plástico alejándose de la cara de la columna al final de la placa de diafragma interna o externa (Figura 4). Ambas conexiones también fueron capaces de alcanzar 0,4 rad. de rotación antes de someterse a pandeo local que resultó en la degradación de la capacidad de momento. Sin embargo, la fractura se inició en la esquina del haz HSS debido al ciclo a grandes niveles de rotación de 0,7 rad. En la Figura 5 se puede ver una comparación de las curvas de rotación de momento normalizadas para las conexiones de placa de diafragma emparejadas y externas. En general, las conexiones reforzadas mostraron ser prometedoras para el uso de sistemas de marco de momento sísmico HSS a HSS, pero se necesita más trabajo para mover estas conexiones hacia una eventual precalificación.

AISC. (2010). «Disposiciones Sísmicas para Edificios de Acero Estructural». ANSI / AISC 341-10. Instituto Americano de Construcción de Acero, Chicago, IL.

AISC. (2010). «Especificaciones para Edificios de Acero Estructural». ANSI / AISC 360-10. Instituto Americano de Construcción de Acero, Chicago, IL.

AWS. (2010). «Código de Soldadura Estructural». ANSI / AWS D1.1, American Welding Society, Miami, FL.

Fadden, F. and McCormick, J. (2014a). «Finite Element Model of the Cyclic Bending Behavior of Hollow Structural Sections». Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. y McCormick, J. (2014b). «HSS-to-HSS Seismic Moment Connection Performance and Design» (en inglés). Journal of Constructional Steel Research, 101, págs. 373 a 384.

Fadden, F., Wei, D., y McCormick, J. (2015). «Pruebas Cíclicas de conexiones de momento Soldadas de HSS a HSS para aplicaciones Sísmicas». ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J. E. M. and Redwood, R. G. (1966). «Diseño de Juntas a Secciones de Caja». The Institution of Structural Engineers, Conferencia sobre la Construcción Industrializada y el Ingeniero Estructural, Instituto de Ingenieros Estructurales, Londres.

Korol, R. M., El-Zanaty, M., and Brady, F. J. (1977). «Unequal Width Connections of Square Hollow Sections in Vierendeel Trusses» (en inglés). Canadian Journal of Civil Engineering, 4, 190-201.Packer, J. A. (1993). «Conexiones de Momento entre Secciones Huecas Rectangulares». Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. y Kurobane, Y. (2010). Guía de Diseño 3: Para Juntas de Sección Hueca Rectangular (RHS) con Carga Predominantemente Estática 2a Edición. CIDECT, Canadá.Wardenier, J. (1982). «Juntas de Sección Hueca». Delft University Press, Delft, Países Bajos.

de septiembre de 2016

Descargar PDF