Proporcione números separados por comas para calcular.

Calculadora de Estadísticas Relacionadas / Calculadora de Desviación Estándar / Calculadora de Tamaño de Muestra

Media

La palabra media, que es un homónimo para varias otras palabras en el idioma inglés, es igualmente ambigua incluso en el área de las matemáticas. Dependiendo del contexto, ya sea matemático o estadístico, lo que se entiende por «media» cambia. En su definición matemática más simple con respecto a los conjuntos de datos, la media utilizada es la media aritmética, también conocida como expectativa matemática, o promedio. En esta forma, la media se refiere a un valor intermedio entre un conjunto discreto de números, a saber, la suma de todos los valores del conjunto de datos, dividida por el número total de valores. La ecuación para calcular una media aritmética es prácticamente idéntica a la para calcular los conceptos estadísticos de media de población y muestra, con ligeras variaciones en las variables utilizadas:

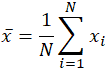
La media a menudo se denota como x, pronunciada «barra x», e incluso en otros usos cuando la variable no es x, la notación de barras es un indicador común de alguna forma de media. En el caso específico de la media de población, en lugar de usar la variable x, se usa el símbolo griego mu, o μ. De manera similar, o más bien confusamente, la media de la muestra en las estadísticas a menudo se indica con una X mayúscula. Dado el conjunto de datos 10, 2, 38, 23, 38, 23, 21, aplicando la suma anterior a los rendimientos:

Como se mencionó anteriormente, este es uno de los más simples definiciones de la media, y algunos otros incluyen la ponderación de la media aritmética (que sólo se diferencia en que ciertos valores en el conjunto de datos de aportar más valor que otros), y la media geométrica. La comprensión adecuada de determinadas situaciones y contextos a menudo puede proporcionar a una persona las herramientas necesarias para determinar qué método estadísticamente relevante usar. En general, lo ideal es que la media, la mediana, el modo y el rango se calculen y analicen para una muestra o conjunto de datos dado, ya que dilucidan diferentes aspectos de los datos dados y, si se consideran por sí solos, pueden dar lugar a tergiversaciones de los datos, como se demostrará en las siguientes secciones.

Mediana

El concepto estadístico de la mediana es un valor que divide una muestra de datos, una población o una distribución de probabilidad en dos mitades. Encontrar la mediana esencialmente implica encontrar el valor en una muestra de datos que tiene una ubicación física entre el resto de los números. Tenga en cuenta que al calcular la mediana de una lista finita de números, el orden de las muestras de datos es importante. Convencionalmente, los valores se enumeran en orden ascendente, pero no hay ninguna razón real por la que enumerar los valores en orden descendente proporcione resultados diferentes. En el caso de que el número total de valores en una muestra de datos sea impar, la mediana es simplemente el número en el medio de la lista de todos los valores. Cuando la muestra de datos contiene un número par de valores, la mediana es la media de los dos valores medios. Si bien esto puede ser confuso, simplemente recuerde que a pesar de que la mediana a veces implica el cálculo de una media, cuando se presenta este caso, solo involucrará los dos valores medios, mientras que una media involucra todos los valores de la muestra de datos. En los casos impares donde solo hay dos muestras de datos o hay un número par de muestras donde todos los valores son iguales, la media y la mediana serán iguales. Dado el mismo conjunto de datos que antes, la mediana se adquiriría de la siguiente manera:

2,10,21,23,23,38,38

Después de enumerar los datos en orden ascendente y determinar que hay un número impar de valores, está claro que 23 es la mediana en este caso. Si hubiera otro valor añadido al conjunto de datos:

2,10,21,23,23,38,38,1027892

Dado que hay un número par de valores, la mediana será el promedio de los dos números medios, en este caso 23 y 23, cuya media es 23. Tenga en cuenta que en este conjunto de datos en particular, la adición de un valor atípico (un valor muy fuera del rango de valores esperado), el valor 1,027,892, no tiene un efecto real en el conjunto de datos. Sin embargo, si se calcula la media para este conjunto de datos, el resultado es 128.505, 875. Este valor claramente no es una buena representación de los otros siete valores en el conjunto de datos que son mucho más pequeños y más cercanos en valor que el promedio y el valor atípico. Esta es la principal ventaja de utilizar la mediana para describir los datos estadísticos en comparación con la media. Mientras que ambos, así como otros valores estadísticos, deben calcularse al describir los datos, si solo se puede usar uno, la mediana puede proporcionar una mejor estimación de un valor típico en un conjunto de datos dado cuando hay variaciones extremadamente grandes entre los valores.

Mode

En estadísticas, el modo es el valor de un conjunto de datos que tiene el mayor número de recurrencias. Es posible que un conjunto de datos sea multimodal, lo que significa que tiene más de un modo. Por ejemplo:

2,10,21,23,23,38,38

Ambos 23 y 38 aparecen dos veces cada uno, convirtiéndolos en un modo para el conjunto de datos anterior.

De manera similar a la media y la mediana, el modo se utiliza como una forma de expresar información sobre variables y poblaciones aleatorias. Sin embargo, a diferencia de la media y la mediana, el modo es un concepto que se puede aplicar a valores no numéricos, como la marca de chips de tortilla que se compran más comúnmente en una tienda de comestibles. Por ejemplo, al comparar las marcas Tostitos, Mission y XOCHiTL, si se descubre que en la venta de chips de tortilla, XOCHiTL es el modo y se vende en una proporción de 3:2:1 en comparación con Tostitos y chips de tortilla de la marca Mission, respectivamente, la proporción se podría usar para determinar cuántas bolsas de cada marca hay en stock. En el caso de que 24 bolsas de chips de tortilla se vendan durante un período determinado, la tienda almacenaría 12 bolsas de chips XOCHiTL, 8 de Tostitos y 4 de Mission si usa el modo. Sin embargo, si la tienda simplemente usaba un promedio y vendía 8 bolsas de cada una, podría perder 4 ventas si un cliente solo deseaba chips XOCHiTL y no cualquier otra marca. Como se desprende de este ejemplo, es importante tener en cuenta todos los tipos de valores estadísticos al intentar sacar conclusiones sobre cualquier muestra de datos.

Rango

El rango de un conjunto de datos en estadísticas es la diferencia entre los valores más grandes y los más pequeños. Mientras el rango tiene diferentes significados en las diferentes áreas de la estadística y las matemáticas, esta es su definición más básica, y es lo que usan la calculadora. Usando el mismo ejemplo:

2,10,21,23,23,38,38
38 – 2 = 36

El rango en este ejemplo es 36. De manera similar a la media, el rango puede verse afectado significativamente por valores extremadamente grandes o pequeños. Usando el mismo ejemplo que antes: