Análisis de regresión lineal en Excel
El tutorial explica los conceptos básicos del análisis de regresión y muestra algunas formas diferentes de hacer regresión lineal en Excel.
Imagine esto: se le proporciona una gran cantidad de datos diferentes y se le pide que prediga las cifras de ventas del próximo año para su empresa. Usted ha descubierto docenas, tal vez incluso cientos, de factores que posiblemente pueden afectar los números. Pero, ¿cómo sabes cuáles son realmente importantes? Ejecute análisis de regresión en Excel. Le dará una respuesta a esta y muchas más preguntas: ¿Qué factores importan y cuáles pueden ignorarse? ¿Qué tan estrechamente están relacionados entre sí estos factores? ¿Y qué tan seguro puedes estar de las predicciones?
- Análisis de regresión en Excel
- Regresión lineal en Excel con Herramienta de análisis
- Dibujar un gráfico de regresión lineal
- Análisis de regresión en Excel con fórmulas
Análisis de regresión en Excel: lo básico
En el modelado estadístico, el análisis de regresión se utiliza para estimar las relaciones entre dos o más variables:
La variable dependiente (también conocida como variable de criterio) es el factor principal que está tratando de entender y predecir.
Las variables independientes (también conocidas como variables explicativas o predictores) son los factores que pueden influir en la variable dependiente.
El análisis de regresión le ayuda a comprender cómo cambia la variable dependiente cuando varía una de las variables independientes y permite determinar matemáticamente cuál de esas variables realmente tiene un impacto.
Técnicamente, un modelo de análisis de regresión se basa en la suma de cuadrados, que es una forma matemática de encontrar la dispersión de los puntos de datos. El objetivo de un modelo es obtener la suma más pequeña posible de cuadrados y dibujar una línea que se acerque más a los datos.
En estadística, diferencian entre una regresión lineal simple y múltiple. Modelos de regresión lineal simple la relación entre una variable dependiente y una variable independiente utilizando una función lineal. Si utiliza dos o más variables explicativas para predecir la variable dependiente, se trata de regresión lineal múltiple. Si la variable dependiente se modela como una función no lineal porque las relaciones de datos no siguen una línea recta, use regresión no lineal en su lugar. El enfoque de este tutorial estará en una regresión lineal simple.
Como ejemplo, tomemos los números de ventas de paraguas de los últimos 24 meses y averigüemos la precipitación mensual promedio para el mismo período. Trace esta información en un gráfico, y la línea de regresión demostrará la relación entre la variable independiente (lluvia) y la variable dependiente (ventas de paraguas):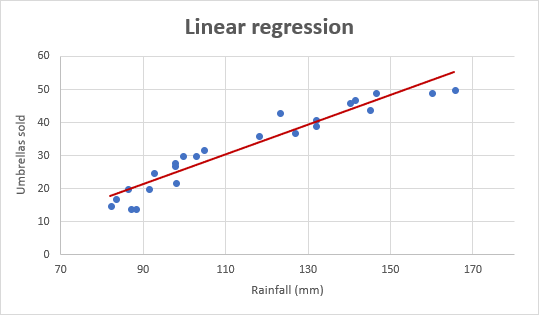
Ecuación de regresión lineal
Matemáticamente, una regresión lineal se define por esta ecuación:
Donde:
- x es una variable independiente.
- y es una variable dependiente.
- a es la intersección Y, que es el valor medio esperado de y cuando todas las variables x son iguales a 0. En un gráfico de regresión, es el punto donde la línea cruza el eje Y.
- b es la pendiente de una línea de regresión, que es la tasa de cambio para y como x cambia.
- ε es el término de error aleatorio, que es la diferencia entre el valor real de una variable dependiente y su valor predicho.
La ecuación de regresión lineal siempre tiene un término de error porque, en la vida real, los predictores nunca son perfectamente precisos. Sin embargo, algunos programas, incluido Excel, hacen el cálculo del término de error entre bastidores. Por lo tanto, en Excel, realiza una regresión lineal utilizando el método de mínimos cuadrados y busca coeficientes a y b tales que:
Para nuestro ejemplo, la ecuación de regresión lineal toma la siguiente forma:
Umbrellas sold = b * rainfall + a
Existen varias formas diferentes de encontrar a y b. Los tres métodos principales para realizar el análisis de regresión lineal en Excel son:
- Herramienta de regresión incluida con la herramienta de análisis \ / li>
- Gráfico de dispersión con una línea de tendencia
- Fórmula de regresión lineal
A continuación encontrará las instrucciones detalladas sobre el uso de cada método.
Cómo hacer regresión lineal en Excel con Análisis ToolPak
Este ejemplo muestra cómo ejecutar regresión en Excel mediante una herramienta especial incluida con el complemento Analysis ToolPak.
Habilitar el complemento Analysis ToolPak
Analysis ToolPak está disponible en todas las versiones de Excel 2019 a 2003, pero no está habilitado de forma predeterminada. Por lo tanto, debe encenderlo manualmente. Aquí le mostramos cómo:
- En su Excel, haga clic en Archivo > Opciones.
- En el cuadro de diálogo Opciones de Excel, seleccione Complementos en la barra lateral izquierda, asegúrese de que Complementos de Excel estén seleccionados en el cuadro Administrar y haga clic en Ir.
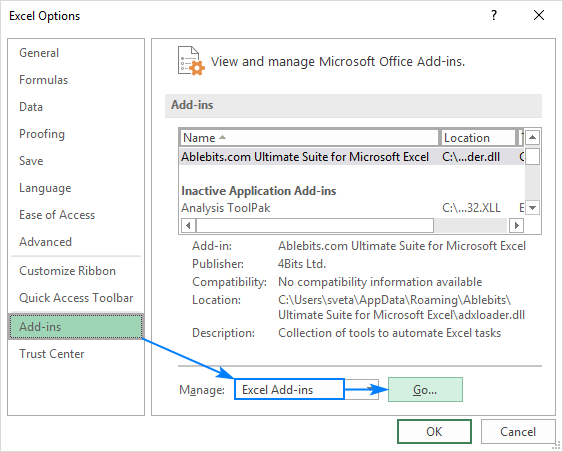
- En el cuadro de diálogo Complementos, marque la casilla Herramienta de análisis y haga clic en Aceptar:
Esto agregará las Herramientas de análisis de datos a la pestaña Datos de su cinta de opciones de Excel.
Ejecutar análisis de regresión
En este ejemplo, vamos a hacer una regresión lineal simple en Excel. Lo que tenemos es una lista de precipitaciones mensuales promedio de los últimos 24 meses en la columna B, que es nuestra variable independiente (predictor), y el número de paraguas vendidos en la columna C, que es la variable dependiente. Por supuesto, hay muchos otros factores que pueden afectar las ventas, pero por ahora nos centramos solo en estas dos variables: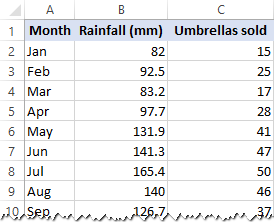
Con la herramienta de análisis añadida habilitada, realice estos pasos para realizar análisis de regresión en Excel:
- En la pestaña Datos, en el grupo Análisis, haga clic en el botón Análisis de datos.
- Seleccione Regresión y haga clic en Aceptar.
- En el cuadro de diálogo Regresión, configure los siguientes parámetros:
- Seleccione el Rango Y de entrada, que es su variable dependiente. En nuestro caso, se trata de ventas de paraguas (C1: C25).
- Seleccione el rango X de entrada, es decir, su variable independiente. En este ejemplo, es la precipitación mensual promedio (B1: B25).
Si está creando un modelo de regresión múltiple, seleccione dos o más columnas adyacentes con diferentes variables independientes.
- Marque la casilla Etiquetas si hay encabezados en la parte superior de los rangos X e Y.
- Elija su opción de salida preferida, una nueva hoja de trabajo en nuestro caso.
- Opcionalmente, seleccione la casilla Residuos para obtener la diferencia entre los valores previstos y reales.
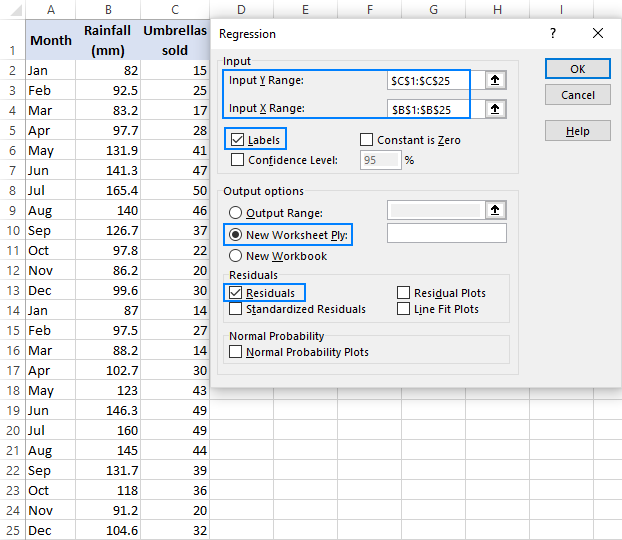
- Haga clic en Aceptar y observe el resultado del análisis de regresión creado por Excel.
Interpretar la salida del análisis de regresión
Como acaba de ver, ejecutar la regresión en Excel es fácil porque todos los cálculos se realizan automáticamente. La interpretación de los resultados es un poco más complicada porque necesitas saber qué hay detrás de cada número. A continuación encontrará un desglose de 4 partes principales del resultado del análisis de regresión.
Salida de análisis de regresión: Salida de resumen
Esta parte le indica qué tan bien se ajusta la ecuación de regresión lineal calculada a los datos de origen.
Esto es lo que significa cada pieza de información:
R múltiple. Es el Coeficiente de Correlación que mide la fuerza de una relación lineal entre dos variables. El coeficiente de correlación puede ser cualquier valor entre -1 y 1, y su valor absoluto indica la fuerza de la relación. Cuanto mayor es el valor absoluto, más fuerte es la relación:
- 1 significa una relación positiva fuerte
- -1 significa una relación negativa fuerte
- 0 significa ninguna relación en absoluto
R Cuadrado. Es el Coeficiente de Determinación, que se utiliza como indicador de la bondad de ajuste. Muestra cuántos puntos caen en la línea de regresión. El valor R2 se calcula a partir de la suma total de cuadrados, más precisamente, es la suma de las desviaciones al cuadrado de los datos originales de la media.
En nuestro ejemplo, R2 es 0.91 (redondeado a 2 dígitos), lo que es muy bueno. Significa que el 91% de nuestros valores se ajustan al modelo de análisis de regresión. En otras palabras, el 91% de las variables dependientes (valores y) se explican por las variables independientes (valores x). En general, R al cuadrado de 95% o más se considera un buen ajuste.
R Cuadrado Ajustado. Es el cuadrado R ajustado para el número de variables independientes en el modelo. Querrá usar este valor en lugar de R cuadrado para el análisis de regresión múltiple.Error estándar
. Es otra medida de bondad de ajuste que muestra la precisión de su análisis de regresión: cuanto más pequeño sea el número, más seguro podrá estar sobre su ecuación de regresión. Mientras que R2 representa el porcentaje de la varianza de las variables dependientes que se explica por el modelo, el error estándar es una medida absoluta que muestra la distancia promedio a la que caen los puntos de datos de la línea de regresión.
Observaciones. Es simplemente el número de observaciones en su modelo.
Análisis de regresión salida: ANOVA
La segunda parte de la salida es Análisis de Varianza (ANOVA):
Básicamente, divide la suma de cuadrados en componentes individuales que proporcionan información sobre los niveles de variabilidad dentro de su modelo de regresión:
- df es el número de grados de libertad asociados con las fuentes de varianza.
- SS es la suma de cuadrados. Cuanto menor sea el SS Residual en comparación con el SS Total, mejor se ajustará su modelo a los datos.
- MS es el cuadrado medio.
- F es la estadística de F, o prueba de F para la hipótesis nula. Se utiliza para probar la importancia general del modelo.
- Significación F es el valor P de F.
La parte ANOVA rara vez se usa para un análisis de regresión lineal simple en Excel, pero definitivamente debe echar un vistazo de cerca al último componente. El valor F de significación da una idea de cuán confiables (estadísticamente significativos) son sus resultados. Si la significación F es inferior a 0,05 (5%), su modelo está bien. Si es mayor que 0.05, probablemente sea mejor elegir otra variable independiente.
Resultados del análisis de regresión: coeficientes
Esta sección proporciona información específica sobre los componentes de su análisis:
El componente más útil de esta sección son los coeficientes. Le permite construir una ecuación de regresión lineal en Excel:
Para nuestro conjunto de datos, donde y es el número de paraguas vendidos y x es una precipitación mensual promedio, nuestra fórmula de regresión lineal es la siguiente:
Y = Rainfall Coefficient * x + Intercept
Equipado con valores a y b redondeados a tres decimales, se convierte en:
Y=0.45*x-19.074
Por ejemplo, con una precipitación mensual promedio igual a 82 mm, las ventas de paraguas serían aproximadamente 17.8:
0.45*82-19.074=17.8
De manera similar, puede averiguar cuántos paraguas se venderán con cualquier otra precipitación mensual (variable x) que especificar.
Resultado del análisis de regresión: residuos
Si compara el número estimado y real de paraguas vendidos correspondiente a la precipitación mensual de 82 mm, verá que estos números son ligeramente diferentes:
- Estimado: 17.8 (calculado arriba)
- Real: 15 (fila 2 de los datos de origen)
¿Por qué la diferencia? Porque las variables independientes nunca son predictores perfectos de las variables dependientes. Y los residuos pueden ayudarlo a comprender cuán lejos están los valores reales de los valores predichos:
Cómo hacer un gráfico de regresión lineal en Excel
Si necesita visualizar rápidamente la relación entre las dos variables, dibuje un gráfico de regresión lineal. Que es muy fácil! Así es como:
- Seleccione las dos columnas con sus datos, incluidos los encabezados.
- En la pestaña de inserción, en el grupo de Chats, haga clic en el icono del gráfico de dispersión y seleccione la miniatura de dispersión (la primera):
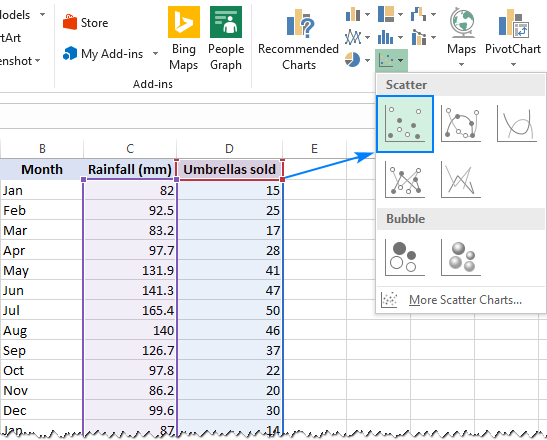
Esto insertará un gráfico de dispersión en su hoja de trabajo, que se parecerá a este:
- Ahora, necesitamos dibujar el gráfico menos línea de regresión de cuadrados. Para hacerlo, haga clic con el botón derecho en cualquier punto y elija Agregar línea de tendencia from en el menú contextual.
- En el panel derecho, seleccione la forma de línea de tendencia lineal y, opcionalmente, marque la ecuación de visualización en el gráfico para obtener su fórmula de regresión:
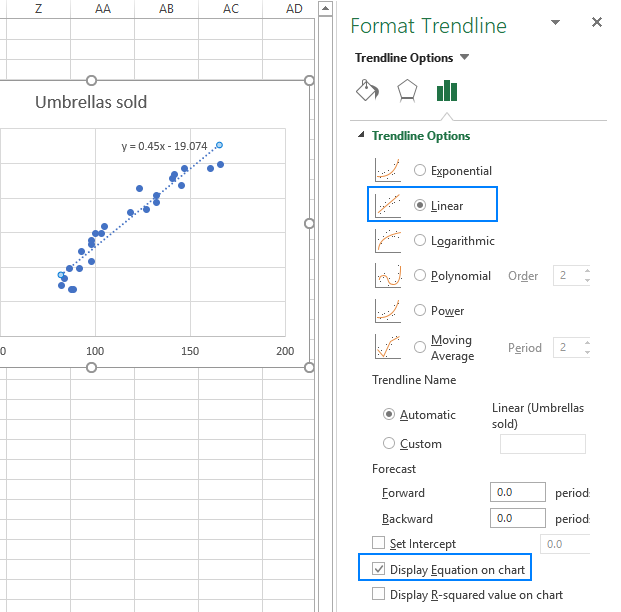
Como puede observar, la ecuación de regresión que Excel ha creado para nosotros es la misma que la fórmula de regresión lineal que construimos en base a la salida de coeficientes.
- Cambie a la pestaña Fill & y personalice la línea a su gusto. Por ejemplo, puede elegir un color de línea diferente y usar una línea sólida en lugar de una línea discontinua (seleccione Línea sólida en el cuadro Tipo guión):
En este punto, su gráfico ya se ve como un gráfico de regresión decente:
Aún así, es posible que desee realizar algunas mejoras más:
- Arrastra la ecuación donde mejor te parezca.
- Añadir títulos de ejes (Botón Elementos de gráfico > Títulos de ejes).
- Si sus puntos de datos comienzan en el centro del eje horizontal y/o vertical, como en este ejemplo, es posible que desee deshacerse del espacio en blanco excesivo. El siguiente consejo explica cómo hacerlo: Escala los ejes del gráfico para reducir el espacio en blanco.
Y así es como se ve nuestro gráfico de regresión mejorado:
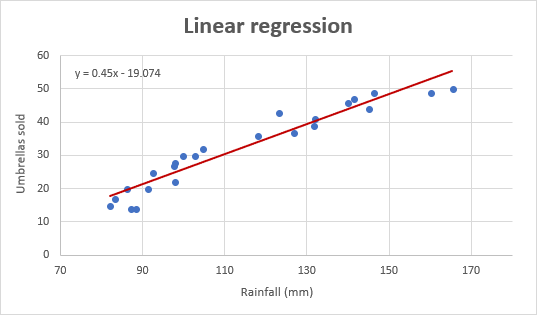¡Nota importante! En el gráfico de regresión, la variable independiente siempre debe estar en el eje X y la variable dependiente en el eje Y. Si su gráfico está trazado en orden inverso, cambie las columnas de su hoja de trabajo y, a continuación, dibuje el gráfico de nuevo. Si no se le permite reorganizar los datos de origen, puede cambiar los ejes X e Y directamente en un gráfico.
Cómo hacer regresión en Excel usando fórmulas
Microsoft Excel tiene algunas funciones estadísticas que pueden ayudarlo a hacer análisis de regresión lineal, como LINEST, SLOPE, INTERCPET y CORREL.
La función LINEST utiliza el método de regresión de mínimos cuadrados para calcular una línea recta que explica mejor la relación entre las variables y devuelve una matriz que describe esa línea. Puede encontrar la explicación detallada de la sintaxis de la función en este tutorial. Por ahora, hagamos una fórmula para nuestro conjunto de datos de muestra:
=LINEST(C2:C25, B2:B25)
Debido a que la función LINEST devuelve una matriz de valores, debe ingresarla como una fórmula de matriz. Seleccione dos celdas adyacentes en la misma fila, E2:F2 en nuestro caso, escriba la fórmula y presione Ctrl + Mayús + Entrar para completarla.
La fórmula devuelve el coeficiente b (E1) y la constante a (F1) para la ecuación de regresión lineal ya familiar:
y = bx + a
Si evita usar fórmulas de matriz en sus hojas de trabajo, puede calcular a y b individualmente con fórmulas regulares:
Obtener la intersección en Y (a):
=INTERCEPT(C2:C25, B2:B25)
Obtener la pendiente (b):
=SLOPE(C2:C25, B2:B25)
Además, puede encontrar el coeficiente de correlación (R múltiple en la salida del resumen del análisis de regresión) que indica la fuerza con la que las dos variables están relacionadas entre sí:
=CORREL(B2:B25,C2:C25)
La siguiente captura de pantalla muestra todas estas fórmulas de regresión de Excel en acción:
Así es como se hace la regresión lineal en Excel. Dicho esto, tenga en cuenta que Microsoft Excel no es un programa estadístico. Si necesita realizar análisis de regresión a nivel profesional, es posible que desee utilizar software específico como XLSTAT,RegressIt, etc.
Descargas disponibles:
Para echar un vistazo más de cerca a nuestras fórmulas de regresión lineal y otras técnicas discutidas en este tutorial, puede descargar nuestro análisis de regresión de muestra en el libro de Excel.
- ¿Cómo utilizar Solver en Excel con ejemplos
- Cómo calcular el interés compuesto en Excel
- Cómo calcular CAGR (tasa de crecimiento anual compuesto) en Excel
Leave a Reply