Energía de la Formación de Enlaces Iónicos

Los enlaces iónicos se forman cuando los iones cargados positiva y negativamente se mantienen unidos por fuerzas electrostáticas. Considere un solo par de iones, un catión y un anión. ¿Cuán fuerte será la fuerza de su atracción? De acuerdo con la Ley de Coulomb, la energía de la atracción electrostática (\(E\)) entre dos partículas cargadas es proporcional a la magnitud de las cargas e inversamente proporcional a la distancia internuclear entre las partículas (\(r\)):

\

\

donde la carga de cada ion está representada por el símbolo Q. La constante de proporcionalidad k es igual a 2,31 × 10-28 J·m. Este valor de k incluye la carga de un solo electrón (1,6022 × 10-19 C) para cada ion. La ecuación también se puede escribir usando la carga de cada ion, expresada en culombios (C), incorporados en la constante. En este caso, la constante de proporcionalidad, k, es igual a 8,999 × 109 J·m/C2. En el ejemplo dado, Q1 = +1(1.6022 × 10-19 C) y Q2 = -1(1.6022 × 10-19 C). Si Q1 y Q2 tienen signos opuestos (como en NaCl, por ejemplo, donde Q1 es +1 para Na+ y Q2 es -1 para Cl−), entonces E es negativo, lo que significa que la energía se libera cuando los iones con carga opuesta se unen desde una distancia infinita para formar un par de iones aislados.

La energía siempre se libera cuando se forma un enlace y, en consecuencia, siempre requiere energía para romper un enlace.

Como se muestra en la curva verde de la mitad inferior de la figura \(\pageIndex{1}\), la energía máxima se liberará cuando los iones estén infinitamente cerca entre sí, a r = 0. Debido a que los iones ocupan espacio y tienen una estructura con el núcleo positivo rodeado de electrones, sin embargo, no pueden estar infinitamente juntos. A distancias muy cortas, las interacciones electrón–electrón repulsivas entre electrones en iones adyacentes se vuelven más fuertes que las interacciones atractivas entre iones con cargas opuestas, como se muestra en la curva roja en la mitad superior de la figura \(\pageIndex{1}\). La energía total del sistema es un equilibrio entre las interacciones atractivas y repulsivas. La curva púrpura de la Figura \(\pageIndex{1}\) muestra que la energía total del sistema alcanza un mínimo en r0, el punto donde las repulsiones electrostáticas y las atracciones están exactamente equilibradas. Esta distancia es la misma que la distancia de enlace medida experimentalmente.

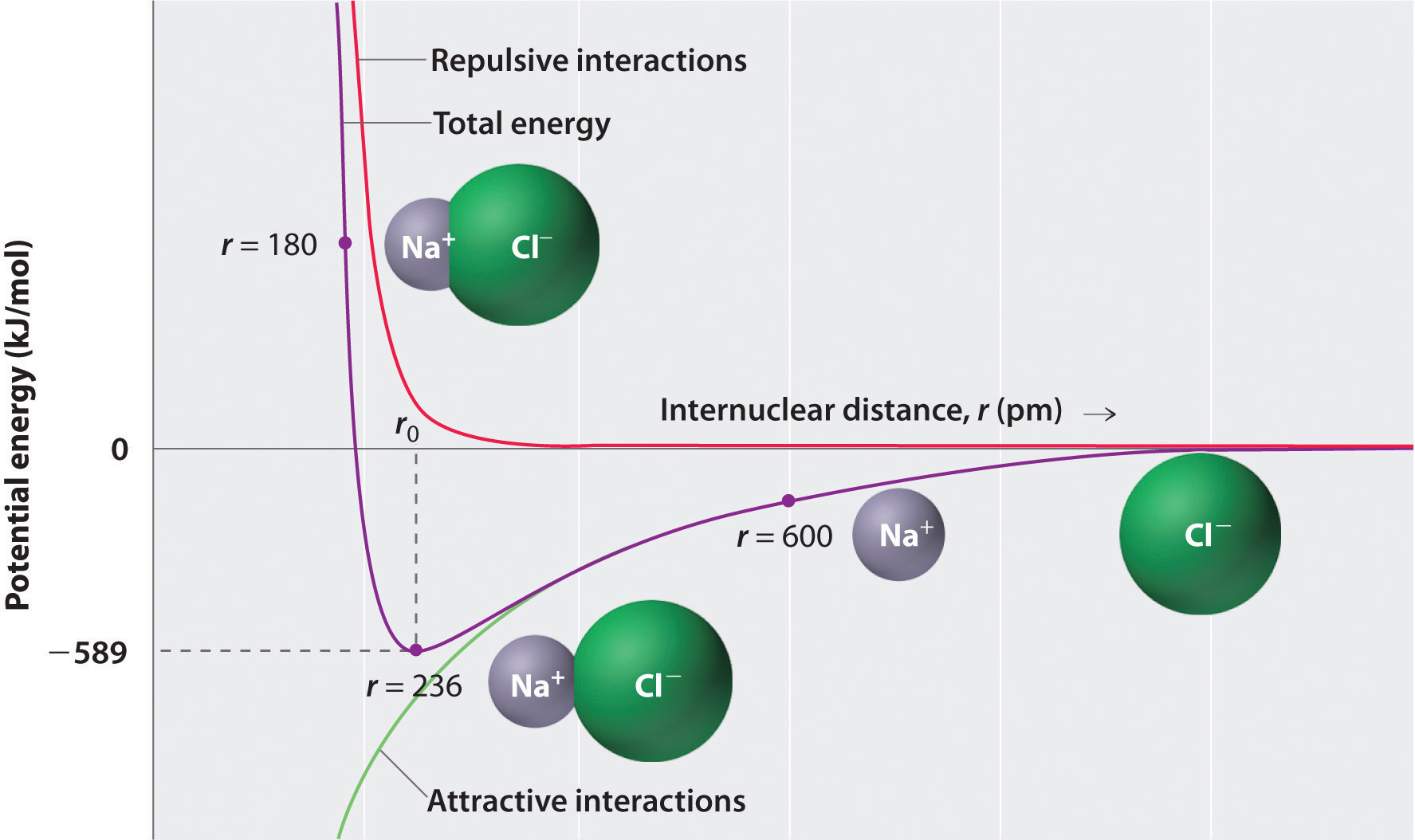
Considere la energía liberada cuando un ion \(Na^+\) gaseoso y un ion \(Cl^-\) gaseoso se unen de r = ∞ a r = r0. Dado que la distancia internuclear de fase gaseosa observada es de 236 pm, el cambio de energía asociado con la formación de un par de iones a partir de un ion \(Na^+_{(g)}\) y un ion \(Cl^-_{(g)}\) es el siguiente:

\ &= (2.31 \times {10^ {- 28}}\rm{J}\cdot \cancel{m} ) \izquierda( \dfrac{( + 1)( – 1)}{236\; \cancel{pm} \ times 10^ {- 12} \cancel{m/pm}} \right) \\ &= – 9.79 \times 10^ {- 19}\; J / ion\; pair \ label{Eq2} \end{align*}\]

El valor negativo indica que se libera energía. Nuestra convención es que si un proceso químico proporciona energía al mundo exterior, el cambio energético es negativo. Si requiere energía, el cambio de energía es positivo. Para calcular el cambio de energía en la formación de un mol de pares de NaCl, necesitamos multiplicar la energía por par de iones por el número de Avogadro:

\

Esta es la energía liberada cuando se forma 1 mol de pares de iones gaseosos, no cuando 1 mol de iones positivos y negativos se condensa para formar una red cristalina. Debido a las interacciones de largo alcance en la estructura de la red, esta energía no se corresponde directamente con la energía de la red del sólido cristalino. Sin embargo, el gran valor negativo indica que unir iones positivos y negativos es energéticamente muy favorable, ya sea que se forme un par de iones o una red cristalina.

Resumimos los puntos importantes sobre la unión iónica:

• En r0, los iones son más estables (tienen una energía potencial menor) que a una distancia internuclear infinita. Cuando los iones con carga opuesta se unen de r = ∞ a r = r0, la energía del sistema se reduce (se libera energía).
• Debido a la baja energía potencial en r0, se debe agregar energía al sistema para separar los iones. La cantidad de energía necesaria es la energía de enlace.
• La energía del sistema alcanza un mínimo a una distancia internuclear particular (la distancia de enlace).