Wird ein altes Problem zu einer neuen Erkenntnis führen? Vielleicht ein eleganter Beweis für den 4-Farben-Satz?
Das 4-Farben-Problem ist eines der bekanntesten mathematischen Probleme. Am Ende gab es einen gültigen Beweis, der sich jedoch auf mehr als tausend Stunden Computerzeit stützte. Jim Tilleys Forschung legt nahe, dass letztendlich eine dramatische Vereinfachung möglich sein könnte. Er hat eine Eigenschaft entdeckt, Kempe-Locking, dass ein minimales Gegenbeispiel zum 4-Farben-Theorem aufweisen muss, und hat eine Vermutung formuliert, basierend auf umfangreichen Untersuchungen, dass der Birkhoff-Diamant die einzige grundlegende Kempe-Locking-Konfiguration ist.
Beim Färben von Graphen werden den Eckpunkten eines mathematischen Objekts, das als Graph bezeichnet wird, Beschriftungen oder Farben zugewiesen. Das 4-Farben-Problem lieferte eine der ursprünglichen Motivationen für die Entwicklung der algebraischen Graphentheorie. Graph Coloring wird bei vielen realen Problemen eingesetzt, z. B. bei der Minimierung von Konflikten bei der Planung von Sportveranstaltungen, der Planung von Prüfungsplänen und der Organisation von Sitzplänen, selbst bei der Platzierung von CCTV-Kameras in einem Gebäude mit vielen Ecken, um Kameraüberschneidungen zu minimieren. Es bietet auch die Grundlage für Sudoku-Rätsel.
Das 4-Farben-Problem
Francis Guthrie, ein Schüler des berühmten britischen Mathematikers und Logikers Augustus De Morgan, stellte 1852 das 4-Farben-Problem. Er formulierte das Problem in Bezug auf Karten, die bestimmte Bedingungen erfüllen, z. B. keine Löcher enthalten und jede Region (z. B. Land oder Bundesstaat) so verbunden ist, dass keine Region in zwei oder mehr nicht zusammenhängenden Teilen existiert. Guthrie behauptete, dass für solche Karten niemals mehr als vier Farben benötigt würden, um die Karte so einzufärben, dass keine zwei benachbarten Regionen dieselbe Farbe hätten.
Heutzutage wird das 4-Farben-Problem in Graphen ausgedrückt, und anstatt Regionen in Karten zu färben, färbt man Eckpunkte in Graphen. Alle vorhandenen Beweise des 4-Farben-Theorems zeigen, dass ein minimales Gegenbeispiel nicht existieren kann. (Ein minimales Gegenbeispiel ist der kleinste planare Graph, der mehr als vier Farben benötigt, um seine Eckpunkte richtig einzufärben.) Nur planare Graphen, die Triangulationen sind, müssen berücksichtigt werden, da jeder Graph, der keine Triangulation ist, durch Einfügen von Kanten in einen Graphen umgewandelt werden kann. Wenn die resultierende Triangulation 4-farbig ist, ist auch der ursprüngliche Graph 4-farbig. Es ist sehr nützlich, die Kontrolle auf Triangulationen beschränken zu können.

Ein früher Versuch des Beweises
Von denen, die einen Beweis anboten, war Alfred Bray Kempe, ein englischer Rechtsanwalt und Amateurmathematiker, die Person, deren Ruf durch seine gescheiterten Bemühungen am stärksten beeinträchtigt wurde. Er kündigte seinen Erfolg im Jahre 1879 und seine ‚Beweis‘ wurde in der American Journal of Mathematics veröffentlicht. Elf Jahre später erstellte jedoch ein anderer englischer Mathematiker, Percy Heawood, eine Karte, die er bis zur endgültigen Region 4-farbig machte, so dass Kempes Methode für diese endgültige Region fehlschlug. Trotz seines Scheiterns hinterließ Kempe ein nützliches Werkzeug – eine Kempe-Kette. Es ist ein maximaler, verbundener Untergraph (jeder Scheitelpunkt ist von jedem anderen durch einen Pfad entlang der Kanten erreichbar), in dem alle Scheitelpunkte genau zwei Farben verwenden. Kempe-Ketten haben sich beim Färben und Neufärben von Graphen als hilfreich erwiesen. Siehe Abbildung 1.
Es wäre eine verblüffende Vereinfachung
wenn der Birkhoff-Diamant allein der Schlüssel zur 4-Farbigkeit wäre. Der erste gültige Beweis wurde 1976 von Kenneth Appel und Wolfgang Haken angekündigt. Es erforderte über tausend Stunden Computerzeit, um bestimmte Aspekte ihrer Argumentation zu überprüfen. Diese Vorstellung, sich auf Computercode zu verlassen, der möglicherweise von Menschen verursachte Fehler enthält (und deren Code!), sondern als ein ‚menschlicher‘ Beweis, hat einen großen Teil der mathematischen Gemeinschaft nicht zufrieden gestellt. Der Beweis von Appel und Haken war in seiner Gesamtstruktur elegant, aber die Details waren hässlich. Der Beweis wurde 1996 von einem Team von vier Mathematikern verfeinert: Robertson, Sanders, Seymour und Thomas, aber sie verließen sich immer noch auf Computercode, um ihren Beweis zu vervollständigen. 2010 bot Steinberger eine weitere Variante an. Es gibt jedoch immer noch keine völlig befriedigende Antwort darauf, warum der 4-Farben-Satz wahr ist. (Sobald die Vermutung bewiesen war, erhielt sie den Status eines Theorems.‘)

und Amateurmathematiker.
Die Suche nach einem alternativen Beweis
Das 4-Farben-Problem ist so einfach zu artikulieren und zu verstehen, dass es das Interesse vieler tausender Amateurmathematiker geweckt hat, die alle glauben, einen einfachen klassischen Beweis finden und so berühmt werden zu können. Jim Tilleys Vater, Physiker und Rektor des kanadischen Royal Military College von 1978-1984, war ein solcher Träumer. Wann immer er das Gefühl hatte, einen Durchbruch erzielt zu haben, bat er seinen Sohn Jim, seine Arbeit zu überprüfen. Jim hat immer einen Fehler gefunden. Doch trotz seiner anfänglichen Skepsis, dass die Bemühungen seines Vaters jemals Früchte tragen würden, wurde er von einer Begeisterung für das 4-Farben-Problem infiziert und begann, es intensiv zu studieren.
Kempe-locking
Jim Tilleys Forschung führte dazu, dass er eine neue Eigenschaft entdeckte, die ein minimales Gegenbeispiel zum 4-Farben-Theorem aufweisen muss. Er nannte es ‘Kempe-Locking. Er erkannte, dass es wahrscheinlich mit einer anderen Eigenschaft unvereinbar war, die ein minimales Gegenbeispiel aufweisen muss – nämlich., wie verbunden ein Diagramm ist (wie viele Eckpunkte müssen aus einem Diagramm entfernt werden, bevor es auseinander fällt).
Tilleys Kempe-Locking ist eine Eigenschaft, die einer Kante in einer Triangulation zugeordnet ist. Der Begriff beginnt mit dem Löschen einer Kante xy zwischen benachbarten Eckpunkten x und y. Wenn es für jede 4-Färbung des resultierenden Graphen, in dem die Farben von x und y gleich sind, keine Folge von Farbaustauschen auf Kempe-Ketten gibt, die bewirkt, dass sich die Farbe von x von der Farbe von y unterscheidet, dann wird die ursprüngliche Triangulation gesagt Kempe-gesperrt in Bezug auf die Kante xy. Tilley bewies, dass ein minimales Gegenbeispiel zum 4-Farben-Theorem in Bezug auf jede seiner Kanten Kempe-gesperrt sein muss; Jede Kante in einem minimalen Gegenbeispiel muss diese Farbeigenschaft haben.
Kempe-Locking ist eine besonders restriktive Bedingung, die schwieriger zu erfüllen ist, wenn eine Triangulation größer wird. Tilley machte sich daran herauszufinden, ob Triangulationen mit Kempe-gesperrten Kanten etwas gemeinsam haben. Seine früheste Suche nach Kempe-Locking führte ihn zum Birkhoff-Diamanten.

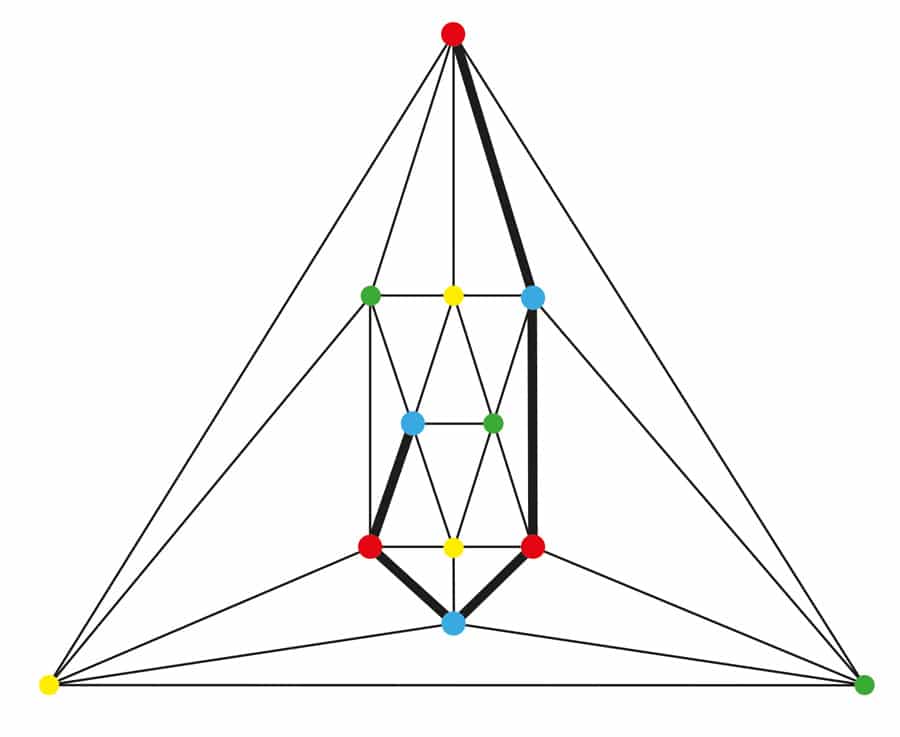
Abbildung 3. Zwei planare Graphen, einer eine 4-verbundene Triangulation auf 6 Eckpunkten und einer eine 5-verbundene Triangulation auf 17 Eckpunkten.
Der Birkhoff-Diamant
1913 entdeckte G. D. Birkhoff, dass eine bestimmte Konfiguration von zehn Ländern auf einer Karte (ein Grenzring aus sechs Ländern, der eine Gruppe von vier Ländern umschließt) eine wichtige Eigenschaft hat. Wenn diese Konfiguration in einer Karte vorhanden ist und die Unterkarte mit dieser entfernten Konfiguration 4-farbig ist, ist die gesamte Karte 4-farbig. Daher kann ein minimales Gegenbeispiel diese bestimmte Konfiguration nicht enthalten. Es wurde als Birkhoff-Diamant bekannt. Tilley fand heraus, dass eine Kempe-verriegelte Kante xy nur dann zu entstehen scheint, wenn x und y auch die Endpunkte der Graphversion eines Birkhoff-Diamanten sind. Siehe Abbildung 2.
Die Vermutung ist leicht zu sagen, verständlich und faszinierend und bietet eine überzeugende Erklärung dafür, warum alle planaren Graphen 4-farbig sind. Da er keine Kempe-Locking-Konfiguration ohne einen Birkhoff-Diamanten gefunden hatte, vermutete er, dass der Birkhoff-Diamant die einzige ‚fundamentale‘ Kempe-Locking-Konfiguration ist, die keine kleinere Kempe-Locking-Konfiguration als Subgraphen enthält. Tilley stellte jedoch fest, dass er seine kritische Vermutung nicht beweisen konnte. Es war frustrierend, weil die Vermutung, wenn sie wahr wäre, den 4-Farben-Satz direkt beweisen würde. (Um ein minimales Gegenbeispiel zu sein, müsste eine Triangulation einen Birkhoff-Diamant-Untergraphen enthalten, aber wenn dies der Fall wäre, könnte es kein minimales Gegenbeispiel sein.)
Ein überwältigender unterstützender Fall
Anstatt seine Vermutung zu beweisen, tat Tilley das nächstbeste. Er beschloss, die Rolle eines Experimentators zu spielen und einen überwältigenden Fall zu erstellen, um seine Vermutung zu stützen. Er teilte alle relevanten planaren Triangulationen in zwei Klassen ein: solche, bei denen mindestens vier Eckpunkte entfernt werden müssen, bevor die Graphen auseinanderfallen (4-verbunden), und solche, bei denen mindestens fünf Eckpunkte entfernt werden müssen, bevor die Graphen auseinanderfallen (5-verbunden). Siehe Abbildung 3. Hilfreich bei Tilleys umfangreicher Suche war, dass er nur ein Mitglied jeder Isomorphismusklasse untersuchen musste (Graphen, die strukturell identisch sind). Tilley untersuchte alle 8.044 Isomorphismusklassen von 4-verbundenen planaren Triangulationen an bis zu 15 Scheitelpunkten und alle 9.733 Isomorphismusklassen von 5-verbundenen planaren Triangulationen an bis zu 24 Scheitelpunkten. Er fand nur drei Kempe-Locked-Triangulationen. Jede entdeckte Kempe-verriegelte Kante wies einen Birkhoff-Diamanten auf und trat jeweils in einer 4-verbundenen Triangulation auf. Es gab überhaupt keine unter 5-verbundenen Triangulationen.

Tilley erweiterte seine Suche unter 4-verbundenen Triangulationen, indem er alle 30.926 Isomorphismusklassen auf 16 Eckpunkten und alle 158.428 Isomorphismusklassen auf 17 Eckpunkten untersuchte. Rechenzeitbeschränkungen bedeuteten, dass er seine Suche auf Stichproben von 100.000 zufällig generierten nicht-isomorphen Triangulationen für Klassen auf 18, 19 und 20 Scheitelpunkten beschränkte. Die erweiterte Suche ergab 45 zusätzliche Kempe-Locked-Triangulationen, aber genau die gleichen Ergebnisse wie die ursprüngliche Suche: Jede Kempe-Locked-Kante in einer Triangulation enthielt einen zugehörigen Birkhoff-Diamanten.
Wo von hier? Tilleys umfangreiche Recherchen bestätigten leicht, dass der Birkhoff Diamond eine grundlegende Kempe-Verriegelungskonfiguration ist. Er hat seine Vermutung gründlich getestet, aber es bleibt unbewiesen. Wenn (oder wenn) sich Tilleys Vermutung bewahrheitet, dass der Birkhoff-Diamant allein der Schlüssel zur 4-Farbigkeit ist, wäre dies eine erstaunliche Vereinfachung des Problems: Eine einzige Konfiguration, die alles erklärt – mathematische Eleganz.

Der Nachweis der 4-Farben-Vermutung erforderte die Bemühungen vieler prominenter Mathematiker. Tilleys Vermutung, dass der Birkhoff-Diamant die einzige grundlegende Kempe-Verriegelungskonfiguration ist, könnte noch schwieriger zu beweisen sein. Die experimentellen Beweise sind jedoch stark. Theoretiker könnten sagen: ‚warum die Mühe? Tilleys Antwort ist, dass unersättliche Neugierde siegen wird: „Schließlich ist die Vermutung leicht zu sagen, verständlich und faszinierend und bietet eine überzeugende Erklärung dafür, warum alle planaren Graphen 4-farbig sind.“
Persönliche Antwort
Was hat Ihre Begeisterung für das 4-Farben-Problem ursprünglich ausgelöst und Sie dazu veranlasst, es so intensiv zu studieren?
Es war die Besessenheit meines Vaters mit dem Problem in seinem Ruhestand und sein Wunsch, mich als Resonanzboden für seine Ideen zu benutzen.
Was sind Ihre Pläne für die zukünftige Forschung in diesem Bereich?
Ich habe kürzlich ein kompliziertes Papier überprüft, das einen völlig anderen Ansatz für das 4-Farben-Problem beinhaltet. Wie das Papier steht, Ich glaube, es hat Mängel. Dennoch hat es Versprechen. Ich könnte versucht sein, eine Zusammenarbeit zu erkunden.
Leave a Reply