Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Einführung
Quadratwurzeln werden am häufigsten mit einem radikalen Zeichen geschrieben, so ![]() . Es gibt jedoch eine andere Möglichkeit, das Nehmen einer Wurzel darzustellen. Sie können rationale Exponenten anstelle eines Radikals verwenden. Ein rationaler Exponent ist ein Exponent, der ein Bruch ist. Zum Beispiel kann
. Es gibt jedoch eine andere Möglichkeit, das Nehmen einer Wurzel darzustellen. Sie können rationale Exponenten anstelle eines Radikals verwenden. Ein rationaler Exponent ist ein Exponent, der ein Bruch ist. Zum Beispiel kann ![]() als
als ![]() geschrieben werden.
geschrieben werden.
Können Sie sich nicht vorstellen, eine Zahl zu einem rationalen Exponenten zu erhöhen? Sie mögen schwer zu gewöhnen sein, aber rationale Exponenten können tatsächlich helfen, einige Probleme zu vereinfachen. Lassen Sie uns die Beziehung zwischen rationalen (gebrochenen) Exponenten und Radikalen untersuchen.
Radikale Ausdrücke mit rationalen Exponenten umschreiben
Radikale und gebrochene Exponenten sind alternative Möglichkeiten, dasselbe auszudrücken. Sie haben bereits gesehen, wie Quadratwurzeln als Exponent zur Potenz der Hälfte ausgedrückt werden können.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Denken Sie daran, das Würfeln einer Zahl erhöht sie auf die Potenz von drei. Beachten Sie, dass in diesen Beispielen der Nenner des rationalen Exponenten die Zahl 3 ist.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and rationale Exponenten: nämlich, dass die n-te Wurzel einer Zahl entweder als ![]() oder
oder ![]() geschrieben werden kann.
geschrieben werden kann.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an ausdruck, der einen rationalen Exponenten enthält, können Sie ihn mit einem Radikal umschreiben. Beachten Sie in der obigen Tabelle, wie der Nenner des rationalen Exponenten den Index der Wurzel bestimmt. Also, ein Exponent von ![]() übersetzt in die Quadratwurzel, ein Exponent von
übersetzt in die Quadratwurzel, ein Exponent von ![]() übersetzt in die fünfte Wurzel oder
übersetzt in die fünfte Wurzel oder ![]() und
und ![]() übersetzt in die achte Wurzel oder
übersetzt in die achte Wurzel oder ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
Antwort |
|
|
Denken Sie daran, dass sich Exponenten nur auf die Menge unmittelbar links von ihnen beziehen, es sei denn, es wird ein Gruppierungssymbol verwendet. Das folgende Beispiel sieht dem vorherigen Beispiel mit einem wichtigen Unterschied sehr ähnlich – es gibt keine Klammern! Schau, was passiert.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Der Nenner des Bruchs bestimmt die Wurzel, in diesem Fall die Kubikwurzel. Der Exponent bezieht sich nur auf den Teil des Ausdrucks unmittelbar links vom Exponenten, in diesem Fall x, aber nicht auf die 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. In diesem Fall ist der Index des Radikals 3, also ist der rationale Exponent Da 4 außerhalb des Radikals liegt, ist es nicht im Gruppierungssymbol enthalten und der Exponent bezieht sich nicht darauf. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
Antwort |
|
|
Rationale Exponenten mit anderen Zählern als einem
Alle Zähler für die gebrochenen Exponenten in den obigen Beispielen waren 1. Sie können gebrochene Exponenten mit anderen Zählern als 1 verwenden, um Wurzeln auszudrücken, wie unten gezeigt. Bemerken Sie irgendwelche Muster in dieser Tabelle?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
chreiben Sie ein Radikal mit einem gebrochenen Exponenten um, die Potenz, auf die der Radikand angehoben wird, wird zum Zähler und die Wurzel zum Nenner.
Schreiben von Bruchexponenten
Jedes Radikal in der Form ![]() kann mit einem Bruchexponenten in der Form
kann mit einem Bruchexponenten in der Form ![]() geschrieben werden.
geschrieben werden.
Die Beziehung zwischen ![]() und
und ![]() funktioniert auch für rationale Exponenten, die einen Zähler von 1 haben. Zum Beispiel kann das Radikal
funktioniert auch für rationale Exponenten, die einen Zähler von 1 haben. Zum Beispiel kann das Radikal ![]() auch als
auch als ![]() geschrieben werden, da jede Zahl den gleichen Wert behält, wenn sie auf die erste Potenz erhöht wird. Sie können jetzt sehen, woher der Zähler von 1 in der äquivalenten Form von
geschrieben werden, da jede Zahl den gleichen Wert behält, wenn sie auf die erste Potenz erhöht wird. Sie können jetzt sehen, woher der Zähler von 1 in der äquivalenten Form von ![]() .
.
Vereinfachung radikaler Ausdrücke mit rationalen Exponenten und den Gesetzen der Exponenten
Lassen Sie uns jetzt einige radikale Ausdrücke untersuchen und sehen, wie sie vereinfacht werden können. Hier ist ein radikaler Ausdruck, der vereinfacht werden muss, ![]() .
.
Eine Methode zur Vereinfachung dieses Ausdrucks besteht darin, Gruppen von a3 zu faktorisieren und herauszuziehen, wie in diesem Beispiel unten gezeigt.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Antwort |
|
|
Sie können diesen Ausdruck auch vereinfachen, indem Sie das Radikal als Ausdruck mit einem rationalen Exponenten betrachten und das Prinzip anwenden, dass jedes Radikal in der Form ![]() mit einem gebrochenen Exponenten geschrieben werden kann in der Form
mit einem gebrochenen Exponenten geschrieben werden kann in der Form ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
Beide Vereinfachungsmethoden ergaben das gleiche Ergebnis, a2. Abhängig vom Kontext des Problems kann es einfacher sein, die eine oder andere Methode zu verwenden, aber im Moment werden Sie feststellen, dass Sie diesen Ausdruck mit rationalen Exponenten schneller vereinfachen konnten als mit der „Pull-out“ -Methode.
Versuchen wir ein anderes Beispiel.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the rationaler Exponent zurück zur radikalen Form. |
|
|
Antwort |
|
|
Auch hier besteht die alternative Methode darin, mit Factoring an der Vereinfachung unter dem Radikal zu arbeiten. Für das Beispiel, das Sie gerade gelöst haben, sieht es so aus.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Antwort ausblenden
Versuchen wir es mit einem komplizierteren Ausdruck, ![]() . Dieser Ausdruck hat zwei Variablen, einen Bruch und ein Radikal. Nehmen wir es Schritt für Schritt und sehen Sie, ob die Verwendung von Bruchexponenten uns helfen kann, es zu vereinfachen.
. Dieser Ausdruck hat zwei Variablen, einen Bruch und ein Radikal. Nehmen wir es Schritt für Schritt und sehen Sie, ob die Verwendung von Bruchexponenten uns helfen kann, es zu vereinfachen.
Beginnen wir mit der Vereinfachung des Nenners, da sich hier das radikale Zeichen befindet.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Konventionell wird ein Ausdruck normalerweise nicht als vereinfacht betrachtet, wenn er einen gebrochenen Exponenten oder ein Radikal im Nenner hat. |
||
|
Antwort |
|
||
Nun, das hat eine Weile gedauert, aber du hast es geschafft. Sie haben das, was Sie über gebrochene Exponenten, negative Exponenten und die Regeln der Exponenten wissen, angewendet, um den Ausdruck zu vereinfachen.
Zusammenfassung
Ein Radikal kann als Ausdruck mit einem gebrochenen Exponenten ausgedrückt werden, indem man der Konvention ![]() folgt. Das Umschreiben von Radikalen mit gebrochenen Exponenten kann nützlich sein, um einige radikale Ausdrücke zu vereinfachen. Denken Sie beim Arbeiten mit gebrochenen Exponenten daran, dass gebrochene Exponenten denselben Regeln unterliegen wie andere Exponenten, wenn sie in algebraischen Ausdrücken vorkommen.
folgt. Das Umschreiben von Radikalen mit gebrochenen Exponenten kann nützlich sein, um einige radikale Ausdrücke zu vereinfachen. Denken Sie beim Arbeiten mit gebrochenen Exponenten daran, dass gebrochene Exponenten denselben Regeln unterliegen wie andere Exponenten, wenn sie in algebraischen Ausdrücken vorkommen.
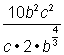
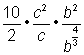
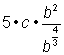
Leave a Reply