Von Jason McCormick
Associate Professor, Civil & Environmental Engineering, University of Michigan, Ann Arbor, MI, USA

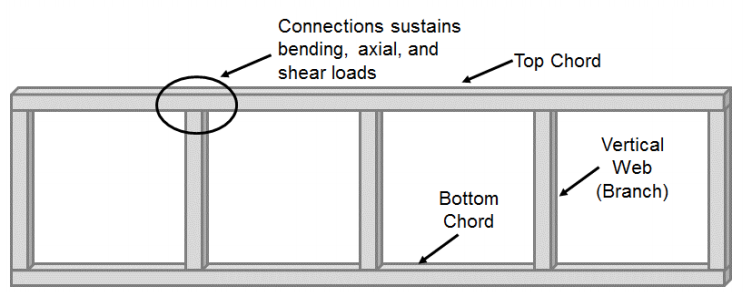
Momentverbindungen aus rechteckigen und quadratischen Hohlprofilen (HSS) wurden im Vergleich zu HSS-zu-HSS-Verbindungen aus axial belasteten Elementen (T-, Y-, Kreuz- und K-Verbindungen) weniger berücksichtigt. Die Mehrheit der statischen Studien, die sich auf diese Verbindungen konzentrieren, haben Vierendeel-Traversensysteme berücksichtigt. Diese Systeme werden häufig durch quadratische oder rechteckige Ober- und Untergurte gebildet, die mit quadratischen oder rechteckigen vertikalen Stegelementen (Verzweigungselementen) verbunden sind (Abbildung 1). Als Ergebnis dieser Konfiguration erfährt die Sehne-zu-Steg-Verbindung eine signifikante Biegung zusammen mit Scher- und Axialbelastungen und wird nicht als Stiftverbindung betrachtet, wie dies üblicherweise in typischen Fachwerksystemen der Fall ist. Ursprünglich 1896 von Arthur Vierendeel konzipiert, wurde erst mit der Entwicklung von HSS das Potenzial für Vierendeel-Traversen erkannt (Korol et al. 1977), aber ihre Verwendung erforderte ein Verständnis dafür, wie Momente zwischen HSS-zu-HSS-T-Verbindungen übertragen werden können.

Viele der frühen Studien dieser Verbindungen konzentrierten sich auf die Fähigkeit der Verbindung, die volle Momentkapazität des Abzweigglieds zu entwickeln. Jubb und Redwood (1966) zeigten, dass bei gleicher Breite des Verzweigungsabschnitts zum Sehnenabschnitt (β = 1) die volle Momentkapazität des HSS-Elements ohne Verstärkung erreicht werden konnte. Diese Studie berücksichtigte jedoch nicht den potenziellen Verlust der Momentenkapazität aufgrund der axialen Belastung. Auf der anderen Seite, Korol et al. (1977) zeigten, dass Verbindungen mit einer kleineren Astbreite als die Sehne nicht die volle Momentenkapazität der Verzweigung ohne Verstärkung durch eine Reihe von 29 verschiedenen Verbindungstests unter Berücksichtigung von 5 verschiedenen Konfigurationen (unverstärkt, Zweigflanschverstärkungsplatten, Akkordflanschversteifungen, Haunch und Pyramidenstumpf) entwickeln konnten. Im Allgemeinen nimmt die Festigkeit und Steifigkeit von unverstärkten Vierendeel-Verbindungen mit einer Zunahme des Sehnenschlankheitsverhältnisses (B / t) und einer Abnahme des Abzweig-zu-Sehnenbreitenverhältnisses (β) ab. Infolgedessen können ungesteifte Vierendeel-Fachwerkverbindungen nur dann als starr angesehen werden (d. h. eine minimale relative Drehung zwischen Sehne und Abzweig erfahren), wenn das Verhältnis von Ast zu Sehne 1,0 beträgt und das Verhältnis von Sehne zu Sehne gering ist oder die Verbindung verstärkt ist (Packer 1993).Da die maximalen Momente in diesen Gelenken bei zu großen Verformungen auftreten können, wird ein ähnlicher Ansatz wie bei axial belasteten quadratischen und rechteckigen HSS-Gelenken gewählt, wobei durch eine endgültige Tragfähigkeit oder eine Verformungs- oder Rotationsgrenze das Konstruktionsmoment charakterisiert wird (Wardenier 1982). AISC 360-10 (Kapitel K3) berücksichtigt drei Grenzzustände für quadratische und rechteckige HSS-T-Verbindungen unter statischer Biegung in der Ebene: Sehnenwandplastifizierung, lokales Nachgeben der Seitenwand und lokales Nachgeben des Zweigs aufgrund ungleichmäßiger Lastverteilung. Die Streckwandplastifizierung erfolgt dadurch, dass die Breite des Abzweiggliedes geringer ist als die Breite der Strecksehne (β ≤ 0,85), so dass die durch das Biegemoment erzeugten Zug- und Druckbelastungen durch die relativ flexible Fläche der Strecksehne und nicht direkt auf die steiferen Seitenwände übertragen werden müssen. Die Grenzzustandsgleichung (AISC 360-10 Gleichung K3-6) kann aus der Fließlinientheorie abgeleitet werden (Abbildung 2):

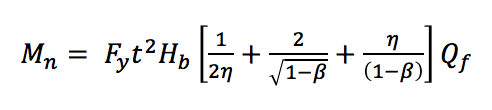
Mn ist die Nennmomentkapazität der Verbindung, Fy ist die angegebene Mindeststreckgrenze der Sehne, Hb ist die Gesamthöhe der Verzweigung, h ist der Parameter für die Lastlänge, der der Höhe der Verzweigung geteilt durch die Breite der Sehne entspricht (unter der Annahme eines Winkels von 90o zwischen Sehne und Verzweigungselement, wie es für Vierendeel-Traversen typisch ist), und Qf ist ein Parameter zur Verringerung der Kapazität des Gelenks bei axialer Kompression in der Sehne.

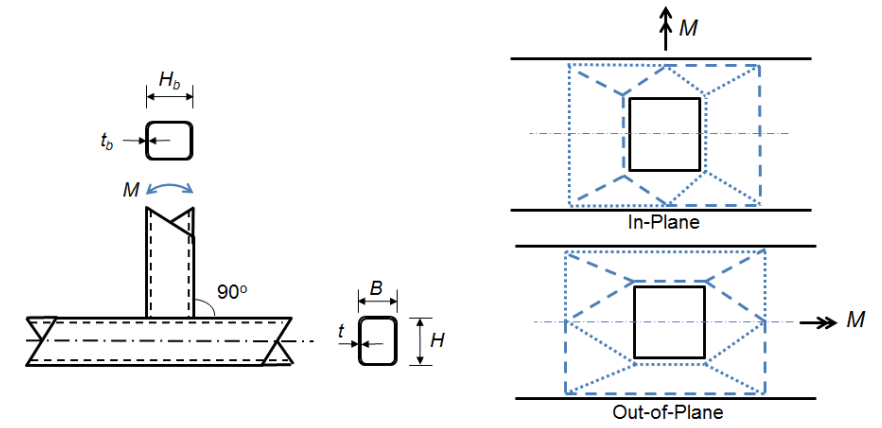
Die anderen beiden Grenzzustände sind Verbindungen zugeordnet, bei denen die Breite des Verzweigungselements gleich oder nahezu gleich der Breite der Sehne ist (β > 0.85), d.h. die in den Flanschen des Abzweiggliedes entstehenden Zug- und Druckbelastungen werden nahezu direkt in die steiferen Seitenwände der Sehne übertragen. Der Grenzzustand für die lokale Nachgiebigkeit der Seitenwand (AISC 360-10-Gleichung K3-7) einer T-Verbindung kann dann aus der lokalen Nachgiebigkeitsgleichung für konzentrierte Kräfte abgeleitet werden, die in einem Abstand vom Ende des Elements aufgebracht werden, der größer als seine Tiefe ist (AISC 360-10-Gleichung J10-2):

Mn = 0.5Fyt(Hb + 5t)2
Gleichung 2

Für das lokale Nachgeben des Zweigs aufgrund einer ungleichmäßigen Lastverteilung (AISC 360-10 Gleichung K3-8) in einer T-Verbindung wird ein effektiver Breitenansatz verwendet, um die Kapazität des Abstützelements zu reduzieren, um das von der Abstützung aufgebrachte Nennmoment zu erhalten:

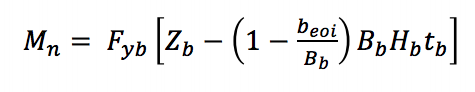
Fyb ist die angegebene Mindeststreckgrenze des Zweigs, Zb ist der Kunststoffquerschnittsmodul des Zweigs um die Biegeachse, beoi ist die effektive Breite des Zweigs, Bb ist die Gesamtbreite des Zweigs und tb ist die konstruktive Wandstärke des Zweigs.

Da es nur begrenzte experimentelle Beweise gibt, um spezifische Designmodelle für Vierendeel-Fachwerkverbindungen (T-Verbindungen) unter Biegung außerhalb der Ebene zu unterstützen, werden analoge Grenzzustände wie für das Biegen in der Ebene verwendet (Packer et al. 2010). Ein weiterer Grenzzustand des Sehnenverzerrversagens ergibt sich aus dem Drehmoment, das das Abzweigglied infolge des Out-of-Plane-Moments auf die Sehne ausübt. Dieses Drehmoment kann zu einer rhomboidalen Verzerrung des Akkords führen. Die Nennmomentgleichungen für das Biegen außerhalb der Ebene finden Sie in den AISC 360-10-Gleichungen K3-9, K3-10, K3-11 und K3-12. Die Gleichungen für das In-Plane- und Out-of-Plane-Biegen von T-Verbindungen ähneln denen, die international übernommen wurden (Packer et al. 2010).

Die obigen Konstruktionsgleichungen wurden unter Berücksichtigung von Vierendeel-Fachwerksystemen unter statischen Belastungen abgeleitet. Eine aktuelle Studie (Fadden et al. 2015) hat diese Arbeit weiterentwickelt, um das Verhalten von quadratischen und rechteckigen HSS-zu-HSS-Momentenverbindungen unter großen zyklischen Belastungen für den Einsatz in rohrbasierten seismischen Momentenrahmensystemen (Zwischen- und Sondermomentenrahmen) zu untersuchen. Ein solches System scheint die hervorragenden Axial-, Biege- und Torsionseigenschaften, das hohe Festigkeits-Gewichts-Verhältnis und die architektonisch ansprechende Natur von quadratischem und rechteckigem HSS zu nutzen. Der hohe Torsionswiderstand kann zu einer Verringerung der lateralen Verstrebung des Trägers führen, während das hohe Verhältnis von Festigkeit zu Gewicht zu einer geringeren seismischen Masse führt. Solche Verbindungen müssen jedoch in der Lage sein, ein stabiles Kunststoffgelenk des Trägerelements zu durchlaufen, wobei 80% der Kunststoffkapazität des Trägerelements entweder auf 0,2 rad gehalten wird. (IWF) oder 0,4 rad. (SMF) von Inter-story Drift (AISC 341-10). Da die derzeitige seismische Konstruktion von Momentrahmensystemen erfordert, dass der Großteil des inelastischen Verhaltens im Trägerelement auftritt, muss das Trägerelement auch seine volle plastische Kapazität erreichen, bevor es lokal geknickt wird. Fadden und McCormick (2014a) berücksichtigten sowohl experimentelle als auch Finite-Elemente-Modelle, um die Anforderungen an die Breite-Dicke und Tiefe-Dicke von HSS unter Biegung zu bestimmen, da die in den aktuellen seismischen Bestimmungen der AISC (AISC 341-10) festgelegten Anforderungen weitgehend auf der Grundlage von Tests mit zyklisch axial belasteten HSS-Elementen entwickelt wurden.

Um geeignete Konfigurations- und Detaillierungsanforderungen zu ermitteln, um diese Anforderungen an Festigkeit und Duktilität zu erfüllen, wurden vier verschiedene Verbindungskonfigurationen experimentell getestet: zwei direkt geschweißte unverstärkte Verbindungen (unübertroffen und abgestimmt) und zwei verstärkte Verbindungen (Durchgangsplatte und externe Membranplatte). Alle Anschlüsse verwendeten eine HSS 10x10x5 / 8-Säule. Die direkt geschweißten Verbindungen verwendeten vorqualifizierte CJP-Schweißnähte gemäß AWS D1.1 (2010). Für die unübertroffene Verbindung war der Strahl ein HSS 12x8x3 / 8 (β = 0.8) was darauf hindeutet, dass die Plastifizierung der Säulenfläche ein Problem sein kann. Für die angepasste Verbindung war der Träger ein HSS 12x10x3 / 8 (β = 1,0), wodurch die Lasten direkt in die Seitenwand übertragen werden konnten. Das AISC-Ladeprotokoll zur Präqualifizierung von seismischen Momentverbindungen wurde verwendet (AISC 341-10), um die Verbindungen zu laden. Das Verhalten der Verbindungen war wie erwartet, wobei die nicht angepasste Verbindung eine Verformung an der Säulenfläche zeigte, während die angepasste Verbindung die Last auf die Säulenseitenwände übertragen konnte. Beide Verbindungen scheiterten jedoch aufgrund eines Bruchs im Grundmetall der Säule an der Spitze der Ecke der Schweißnaht (Abbildung 3). Dieses spröde Versagen bei Umdrehungen von 0,4 rad. und 0,5 rad. bestätigt, dass direkt geschweißte Verbindungen nicht das geeignete Verhalten für seismische Anwendungen bieten.

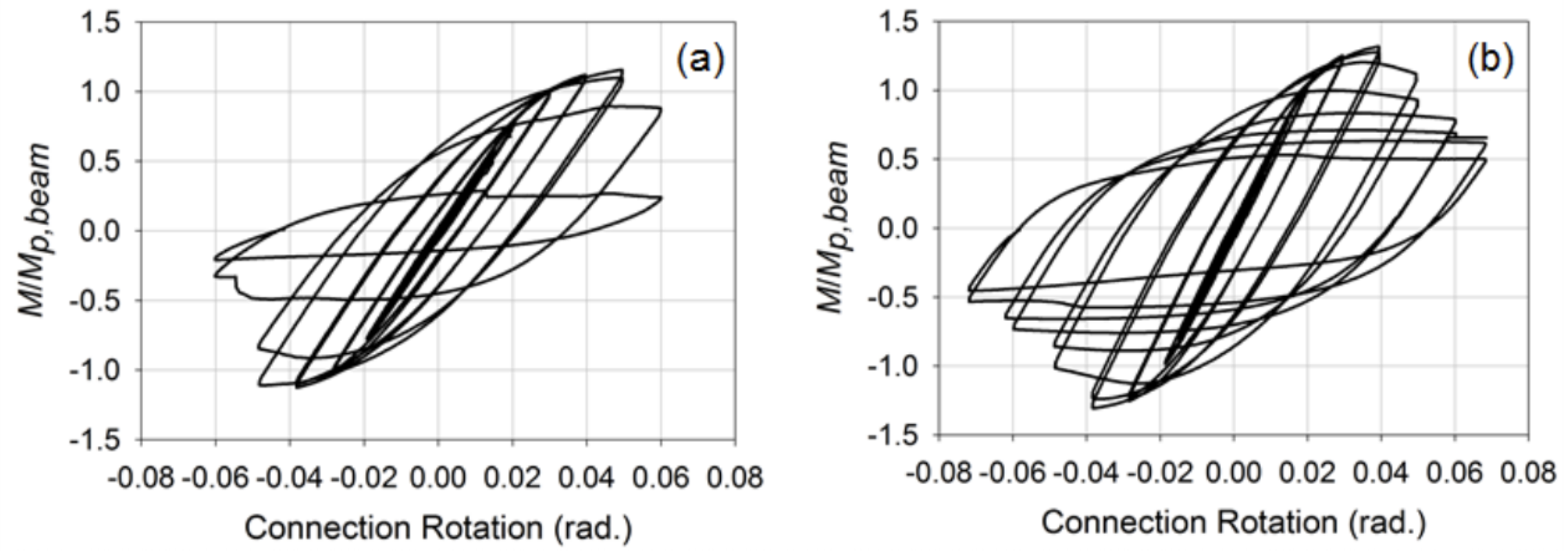
Die verstärkten Verbindungen wurden dann unter Berücksichtigung von Platten- und externen Membranplatten entwickelt, die häufig in Breitflansch-Balken-HSS-Säulenverbindungen verwendet werden, um einen besseren Mechanismus zur Übertragung der Zug- und Druckkräfte auf die Seitenwand der Säule bereitzustellen und Spannungskonzentrationen auf die Schweißnähte zu minimieren. Für diese Verbindungen wurden die Balken HSS 12x8x3 / 8 (β = 0,8) Mitglieder. Informationen zu dem spezifischen Verfahren, mit dem diese Verbindungen entworfen und detailliert werden, finden Sie in Fadden and McCormick (2014b) und Fadden et al. (2015). Bei gleicher Belastung wie die unverstärkten Verbindungen zeigten die Verbindungen ein stabileres Verhalten, wobei das Kunststoffscharnier von der Säulenfläche weg am Ende der durchgehenden oder externen Membranplatte auftrat (Abbildung 4). Beide Verbindungen konnten auch 0,4 rad erreichen. lokalen Knickung, die zu einer Verschlechterung der Momentenkapazität führte. Der Bruch begann jedoch an der Ecke des HSS-Balkens aufgrund von Zyklen bei großen Rotationsniveaus von 0,7 rad. Ein Vergleich der normierten Moment-Dreh-Kurven für die internen und externen Membranplattenanschlüsse ist in Abbildung 5 zu sehen. Insgesamt zeigten sich die verstärkten Verbindungen vielversprechend für die Verwendung von HSS-zu-HSS-seismischen Momentrahmensystemen, aber es ist mehr Arbeit erforderlich, um diese Verbindungen in Richtung einer eventuellen Präqualifikation zu bewegen.

AISC. (2010). „Seismische Bestimmungen für Stahlbaugebäude“. ANSI/AISC 341-10. Amerikanisches Institut für Stahlbau, Chicago, IL.In:

AISC. (2010). „Spezifikationen für Baustahlgebäude“. ANSI/AISC 360-10. Amerikanisches Institut für Stahlbau, Chicago, IL.

AWS. (2010). „Structural Welding Code“. ANSI/AWS D1.1, Amerikanische Schweißensgesellschaft, Miami, FL.

F. und McCormick, J. (2014a). „Finite-Elemente-Modell des zyklischen Biegeverhaltens von Hohlprofilen“. Zeitschrift für Baustahlforschung, 94, 64-75.

Fadden, F. und McCormick, J. (2014b). „HSS-zu-HSS Seismische Moment Verbindung Leistung und Design“. Zeitschrift für Baustahlforschung, 101, 373-384.

Fadden, F., Wei, D. und McCormick, J. (2015). „Zyklische Prüfung von geschweißten HSS-zu-HSS-Momentverbindungen für seismische Anwendungen“. ASCE Zeitschrift für Bauingenieurwesen, 141 (2), 04014109-1-14.

Jubb, J.E.M. und Redwood, R.G. (1966). „Entwurf von Verbindungen zu Kastenprofilen“. Die Institution of Structural Engineers, Konferenz über industrialisierte Gebäude und der Bauingenieur, Institut für Bauingenieure, London.

Korol, R.M., El-Zanaty, M. und Brady, F.J. (1977). „Ungleiche Breite Verbindungen von quadratischen Hohlprofilen in Vierendeel Traversen“. Kanadisches Journal für Bauingenieurwesen, 4, 190-201.

Packer, J.A. (1993). „Momentverbindungen zwischen rechteckigen Hohlprofilen“. Zeitschrift für Baustahlforschung, 25, 63-81.

Packer, J.A., Wardenier, J., Zhao, X.-L., van der Vegte, G.J. und Kurobane, Y. (2010). Design Guide 3: Für Rechteckige Hohlprofil (RHS) Gelenke unter Überwiegend Statische Belastung 2nd Edition. CIDECT, Kanada.

Wardenier, J. (1982). „Hohlprofilverbindungen“. Delft University Press, Delft, Niederlande.

September 2016

PDF herunterladen