Der Graph einer linearen Ungleichung in einer Variablen ist eine Zahlenlinie. Verwenden Sie einen offenen Kreis für < und > und einen geschlossenen Kreis für ≤ und ≥.

Der Graph für x > -3

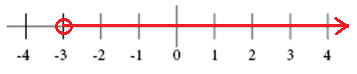
Der Graph für x ≥ 2

Ungleichungen, die die gleiche Lösung haben, werden als äquivalent. Es gibt Eigenschaften von Ungleichheiten, ebenso wie es Eigenschaften von Gleichheit gab. Alle folgenden Eigenschaften gelten auch für Ungleichungen mit ≥ und ≤.

Die Additionseigenschaft der Ungleichung besagt, dass das Hinzufügen derselben Zahl zu jeder Seite der Ungleichung eine äquivalente Ungleichung erzeugt

$$If \: x>y,\: then\: x+z>y+z$$

$$If\: x<y,\: dann\: x+z<y+z$$

Die Subtraktionseigenschaft der Ungleichung sagt uns, dass das Subtrahieren derselben Zahl von beiden Seiten einer Ungleichung eine äquivalente Ungleichung ergibt.

$$Wenn \: x>y,\: dann\: x-z>y-z$$

$$Wenn\: x<y,\: dann\: x-z<y-z$$

Die Multiplikationseigenschaft der Ungleichung sagt uns, dass die Multiplikation auf beiden Seiten einer Ungleichung mit einer positiven Zahl eine äquivalente Ungleichung erzeugt.

$$If \: x>y \: und\: z>0,\: dann\: xz>yz$$

$$Wenn\: x<y\: und\: z>0,\: dann\: xz<yz$$

Die Multiplikation auf jeder Seite einer Ungleichung mit einer negativen Zahl erzeugt andererseits keine äquivalente Ungleichung, es sei denn, wir kehren auch die Richtung des Ungleichungssymbols um

$$If \: x>y \: and\: z<0,\: then\: xz<yz$$

$$Wenn\: x<y\: und\: z<0,\: then\: xz>yz$$

Das gleiche gilt für die Divisionseigenschaft der Ungleichung.

Die Division beider Seiten einer Ungleichung mit einer positiven Zahl erzeugt eine äquivalente Ungleichung.

$$If \: x>y \: und\: z>0,\: dann\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x<y\: und\: z>0,\: dann\: \frac{x}{z}<\frac{y}{z}$$

Und Division auf beiden Seiten einer Ungleichung mit einer negativen Zahl erzeugt eine äquivalente Ungleichung, wenn das Ungleichheitssymbol umgekehrt ist.

$$Wenn \: x>y \: und\: z<0,\: dann\: \frac{x}{z}<\frac{y}{z}$$

$$Wenn\: x<y\: and\: z<0,\: then\: \frac{x}{z}>\frac{y}{z}$$

Um eine mehrstufige Ungleichung zu lösen, gehen Sie wie beim Lösen von mehrstufigen Gleichungen vor. Nehmen Sie eine Sache zu der Zeit, vorzugsweise zu Beginn, indem Sie die Variable von den Konstanten isolieren. Bei der Lösung von mehrstufigen Ungleichungen ist es wichtig, nicht zu vergessen, das Ungleichheitszeichen umzukehren, wenn Sie mit negativen Zahlen multiplizieren oder dividieren.

Beispiel

Lösen Sie die Ungleichung

$$-2\left ( x+3 \right )<10$$