Komplexe Zahlen: Einführung (Seite 1 von 3)

Abschnitte: Einführung, Operationen mit Komplexen, Die quadratische Formel

Bis jetzt wurde Ihnen gesagt, dass Sie dass Sie nicht die Quadratwurzel einer negativen Zahl nehmen können. Das liegt daran, dass Sie keine Zahlen hatten, die negativ waren, nachdem Sie sie quadriert hatten (Sie konnten also nicht „rückwärts gehen“, indem Sie die Quadratwurzel nahmen). Jede Zahl war positiv, nachdem Sie sie quadriert hatten. Sie könnten also nicht sehr gut ein Negativ quadratwurzeln und erwarten, etwas Vernünftiges zu finden.

Jetzt können Sie jedoch die Quadratwurzel einer negativen Zahl nehmen, aber dazu müssen Sie eine neue Zahl verwenden. Diese neue Nummer wurde erfunden (entdeckt?) um die Zeit der Reformation. Zu dieser Zeit glaubte niemand, dass für diese neue Zahl eine „reale“ Verwendung gefunden werden würde, außer die Berechnungen zur Lösung bestimmter Gleichungen zu erleichtern, so dass die neue Zahl als eine aus Gründen der Bequemlichkeit erfundene Scheinzahl angesehen wurde.

(Aber wenn Sie darüber nachdenken, sind nicht alle Zahlen Erfindungen? Es ist nicht so, dass Zahlen auf Bäumen wachsen! Sie leben in unseren Köpfen. Wir haben sie alle erfunden! Warum nicht ein neues erfinden, solange es mit dem, was wir bereits haben, gut funktioniert?)

Dann:

kann dies tun:

Aber das macht keinen Sinn! Sie haben bereits zwei Zahlen, die zu 1 quadrieren; nämlich -1 und +1. Und ich habe bereits Quadrate zu -1. Es ist also nicht vernünftig, dass ich auch zu 1 quadrieren würde. Dies weist auf ein wichtiges Detail hin: Im Umgang mit Imaginären gewinnen Sie etwas (die Fähigkeit, mit Negativen innerhalb von Quadratwurzeln umzugehen), aber Sie verlieren auch etwas (einige der Flexibilität und praktischen Regeln, die Sie früher im Umgang mit Quadratwurzeln hatten). Insbesondere MÜSSEN SIE IMMER ZUERST DEN i-TEIL MACHEN!

• Vereinfachen Sie sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Alle Rechte vorbehalten

(Warnung: Der Schritt, der durch das dritte Gleichheitszeichen geht, ist “ „, nicht „„. Das Ich ist außerhalb des Radikalen.)

• Vereinfachen Sie sqrt(-25).

• Vereinfachen Sie sqrt(-18).

• Vereinfache –sqrt(-6).

In Ihren Berechnungen werden Sie mit i genauso umgehen wie mit x , mit Ausnahme der Tatsache, dass x2 nur x2 ist, aber i2 ist -1:

• Vereinfachen Sie 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Vereinfachen Sie 16i – 5i.

16i – 5i = (16 – 5)i = 11i

• Multiplizieren und vereinfachen (3i)(4i).

(3i)(4i) = (3 · 4)(ich ·ich) = (12)(i2) = (12)(-1) = -12

• Multiplizieren und vereinfachen Sie (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

Beachten Sie dieses letzte Problem. Darin können Sie sehen, dass , weil i2 = -1 . Wenn wir fortfahren, erhalten wir:

Dieses Muster von Potenzen, Zeichen, 1 und i ist ein Zyklus:

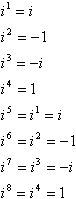
Mit anderen Worten, um eine hohe Potenz von i zu berechnen, können Sie sie in eine niedrigere Potenz umwandeln, indem Sie das nächste von 4 ist das nicht größer als der Exponent und subtrahiert dieses Vielfache vom Exponenten. Zum Beispiel ist eine häufige Trickfrage zu Tests etwas in der Art von „Simplify i99“, die Idee ist, dass Sie versuchen werden, i neunundneunzig Mal zu multiplizieren, und Sie werden keine Zeit mehr haben, und die Lehrer werden ein gutes Kichern auf Ihre Kosten in der Fakultätslounge bekommen. Hier ist, wie die Verknüpfung funktioniert:

i99 = i96+3 = i(4× 24)+3 = i3 = –i

Das heißt, i99 = i3, weil Sie nur die i96 lop aus. (Sechsundneunzig ist ein Vielfaches von vier, also ist i96 nur 1, was Sie ignorieren können.) Mit anderen Worten, Sie können den Exponenten durch 4 dividieren (mit langer Division), die Antwort verwerfen und nur den Rest verwenden. Dies gibt Ihnen den Teil des Exponenten, den Sie interessieren. Hier noch ein paar Beispiele:

• Simplify i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• Vereinfachen Sie i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Vereinfachen Sie i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>