Purplemath

Der „Interquartilbereich“, abgekürzt „IQR“, ist nur die Breite der Box im Box-and-Whisker-Plot. Das heißt, IQR = Q3 – Q1 . Der IQR kann als Maß dafür verwendet werden, wie weit die Werte verteilt sind.

Statistics geht davon aus, dass Ihre Werte um einen zentralen Wert gruppiert sind. Der IQR gibt an, wie weit die „mittleren“ Werte verteilt sind; Es kann auch verwendet werden, um festzustellen, wann einige der anderen Werte „zu weit“ vom zentralen Wert entfernt sind. Diese „zu weit entfernten“ Punkte werden „Ausreißer“ genannt, weil sie „außerhalb“ des Bereichs liegen, in dem wir sie erwarten.

Der IQR ist die Länge der Box in Ihrem Box-and-Whisker-Plot. Ein Ausreißer ist jeder Wert, der mehr als das Anderthalbfache der Länge der Box von beiden Enden der Box liegt.

Der Inhalt wird weiter unten fortgesetzt

MathHelp.com

Das heißt, wenn ein Datenpunkt unter Q1 – 1,5 ×IQR oder über Q3 + 1,5×IQR liegt, wird er als zu weit von den zentralen Werten entfernt angesehen, um angemessen zu sein. Vielleicht haben Sie die Waage gestoßen, als Sie diese eine Messung durchgeführt haben, oder vielleicht ist Ihr Laborpartner ein Idiot und Sie hätten ihn niemals eines der Geräte berühren lassen sollen. Wer weiß? Aber was auch immer ihre Ursache ist, die Ausreißer sind die Punkte, die nicht zu „passen“ scheinen.

Sobald Sie den IQR gefunden haben, können Sie mit dem Auffinden der Ausreißer fortfahren, falls vorhanden.

• Finden Sie die Ausreißer, falls vorhanden, für den folgenden Datensatz:

Die Werte für Q1 – 1.5×IQR und Q3 + 1.5 × IQR sind die „Zäune“, die die „vernünftigen“ Werte von den Ausreißerwerten abgrenzen. Ausreißer liegen außerhalb der Zäune.

Wenn Sie bei Ihrer Aufgabe nicht nur Ausreißer, sondern auch „Extremwerte“ berücksichtigen müssen, sind die Werte für Q1 – 1,5 ×IQR und Q3 + 1,5×IQR die „inneren“ Zäune und die Werte für Q1 – 3 ×IQR und Q3 + 3 ×IQR sind die „äußeren“ Zäune.

Die Ausreißer (markiert mit Sternchen oder offenen Punkten) befinden sich zwischen den inneren und äußeren Zäunen, und die Extremwerte (markiert mit dem Symbol, das Sie nicht für die Ausreißer verwendet haben) befinden sich außerhalb der äußeren Zäune.

Übrigens kann Ihr Buch den Wert von “ 1,5 ×IQR “ als „Schritt“ bezeichnen. Dann sind die Ausreißer die Zahlen, die zwischen einem und zwei Schritten von den Scharnieren entfernt sind, und der Extremwert sind die Zahlen, die mehr als zwei Schritte von den Scharnieren entfernt sind.

Wenn man sich das vorherige Beispiel noch einmal ansieht, wären die äußeren Zäune bei 14,4 – 3 × 0,5 = 12,9 und 14,9 + 3 × 0,5 = 16,4. Da 16.4 direkt am oberen äußeren Zaun liegt, würde dies nur als Ausreißer und nicht als Extremwert angesehen. Aber 10.2 liegt vollständig unter dem unteren äußeren Zaun, also wäre 10.2 ein Extremwert.

Ihr Grafikrechner zeigt möglicherweise an, ob ein Box-and-Whisker-Diagramm Ausreißer enthält oder nicht. Zum Beispiel enthält das obige Problem die Punkte 10.2, 15.9 und 16.4 als Ausreißer. Eine Einstellung in meinem Grafikrechner ergibt das einfache Box-and-Whisker-Diagramm, das nur die Zusammenfassung mit fünf Zahlen verwendet, sodass die am weitesten entfernten Ausreißer als Endpunkte der Whisker angezeigt werden:

Eine andere Rechner-Einstellung gibt den Box-and-Whisker-Plot mit den speziell markierten Ausreißern (in diesem Fall mit einer Simulation eines offenen Punktes), und die Whisker gehen nur bis zu den höchsten und niedrigsten Werten, die keine Ausreißer sind:

Mein Rechner unterscheidet nicht zwischen Ausreißern und Extremwerten. Deine vielleicht auch nicht. Überprüfen Sie jetzt Ihre Bedienungsanleitung, bevor Sie den nächsten Test durchführen.

Wenn Sie Ihren Grafikrechner verwenden, um mit diesen Plots zu helfen, stellen Sie sicher, dass Sie wissen, welche Einstellung Sie verwenden sollen und was die Ergebnisse bedeuten, oder der Rechner kann Ihnen eine vollkommen richtige, aber „falsche“ Antwort geben.

• Finden Sie die Ausreißer und Extremwerte, falls vorhanden, für den folgenden Datensatz, und zeichnen Sie das Box-and-Whisker-Diagramm. Markieren Sie Ausreißer mit einem Sternchen und Extremwerte mit einem offenen Punkt.

Werbung

Um die Ausreißer und Extremwerte zu finden, muss ich zuerst den IQR finden. Da die Liste sieben Werte enthält, ist der Median der vierte Wert, also:

Q2 = 25

Die erste Hälfte der Liste ist:

21, 23, 24

…also Q1 = 23; die zweite Hälfte ist:

29, 33, 49

…also Q3 = 33. Dann wird der IQR gegeben durch:

IQR = 33 – 23 = 10

Die Ausreißer sind alle folgenden Werte:

23 – 1.5×10 = 23 – 15 = 8

…oder höher:

33 + 1.5×10 = 33 + 15 = 48

Die Extremwerte sind die folgenden:

23 – 3×10 = 23 – 30 = -7

…oder höher:

33 + 3×10 = 33 + 30 = 63

Ich habe also einen Ausreißer bei 49, aber keine Extremwerte. Ich werde keinen Top-Whisker auf meinem Grundstück haben, da Q3 auch der höchste Nicht-Ausreißer ist. Mein Plot sieht also so aus:

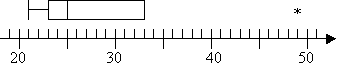
Es sollte beachtet werden, dass die oben beschriebenen Methoden, Begriffe und Regeln das sind, was ich gelehrt habe und was ich am häufigsten gelehrt habe. Ihr Kurs kann jedoch unterschiedliche spezifische Regeln haben, oder Ihr Taschenrechner kann Berechnungen etwas anders durchführen. Möglicherweise müssen Sie etwas flexibel sein, um die für Ihren Lehrplan spezifischen Antworten zu finden.