Die Erhaltung des Impulses ist ein grundlegendes Konzept der Physik, zusammen mit der Erhaltung der Energie und der Erhaltung der Masse.Der Impuls ist definiert als die Masse eines Objekts multipliziert mit der Geschwindigkeit des Objekts.Die Impulserhaltung besagt, dass innerhalb eines Problembereichs die Impulsmenge konstant bleibt;der Impuls wird weder erzeugt noch zerstört, sondern nur durch die Einwirkung von Kräften verändert, wie sie durch Newtons Bewegungsgesetze beschrieben werden.Der Umgang mit Impulsen ist schwieriger als der Umgang mit Masse und Energie, da das Moment eine Vektorgröße ist, die sowohl eine Größe als auch eine Richtung hat. Der Impuls bleibt in allen dreiphysikalische Richtungen gleichzeitig. Es ist noch schwieriger, wenn es um Agas gehtweil Kräfte in einer Richtung den Impuls in eine andere Richtung beeinflussen könnenwegen der Kollisionen vieler Moleküle.Auf dieser Folie stellen wir ein sehr, sehr vereinfachtes Fließproblem vor, bei dem sich die Eigenschaften nur in eine Richtung ändern.Das Problem wird weiter vereinfacht, indem eine stetige Strömung in Betracht gezogen wird, die sich nicht mit der Zeit ändert, und indem die Kräfte auf nur die Kräfte begrenzt werden, die mit thepressure.Be sich bewusst, dass reale Strömungsprobleme viel komplexer sindals dieses einfache Beispiel.

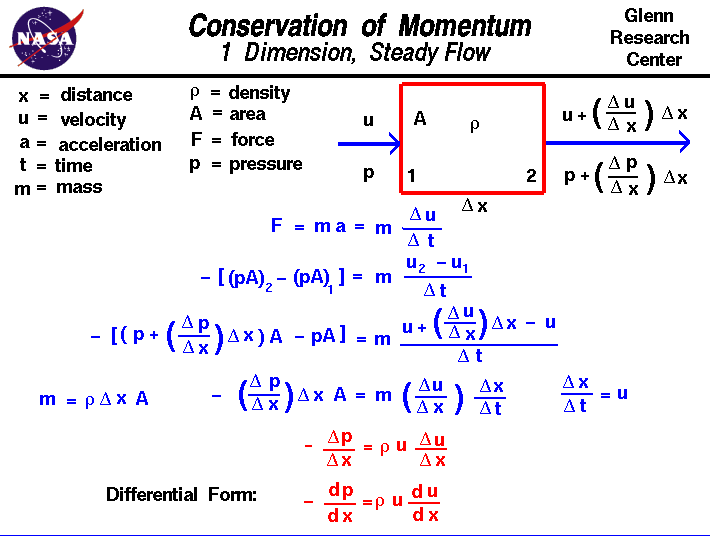
Betrachten wir den Fluss eines Gases durch eine Domäne, in der sich Strömungseigenschaftennur in eine Richtung ändern, die wir „x“ nennen werden. Das Gas tritt an der Station 1 mit einer gewissen Geschwindigkeit u und einem gewissen Druck p in die Domäne ein und tritt an der Station 2 mit einem anderen Geschwindigkeits- und Druckwert aus. Der Einfachheit halber gehen wir davon aus, dassdie Dichte r innerhalb der Domäne konstant bleibt und dass der Bereich A, durch den das Gas fließt, ebenfalls konstant bleibt. Die position der stationen 1 und 2 sind separatedby ein abstand genannt del x. (Delta ist die kleine dreieck auf die slideand ist die Griechischen buchstaben „d“. Mathematiker verwenden dieses Symbol häufig zur bezeichnungeine Änderung oder Variation einer Größe. Die Web Print Schriftart unterstützt nichtdie griechischen Buchstaben, also nennen wir es einfach „del“.) Eine Änderung mit der Entfernung wird als Gradient bezeichnet, um Verwechslungen mit einer Änderung mit der Zeit zu vermeiden, die als Rate bezeichnet wird.Der Geschwindigkeitsgradient wird durch del u / del x angegeben;die Änderung der Geschwindigkeit pro Entfernungsänderung. An Station 2 ist die Geschwindigkeit also durch die Geschwindigkeit bei 1 plus der Steigung mal der Entfernung gegeben.

Ein ähnlicher Ausdruck gibt den Druckam Ausgang:

Newtons zweites Bewegungsgesetz besagt, dass die Kraft F gleich der Änderung des Impulses in Bezug auf die Zeit ist. Für ein Objekt mit konstanter Masse reduziert sich dies auf die Masse mal Beschleunigung a.An beschleunigung ist eine Geschwindigkeitsänderung mit einer Zeitänderung(del u / del t). Dann:

Die Kraft in diesem Problemkommt aus dem Druckgradienten. Da Druck eine Kraft pro Flächeneinheit ist, ist die Nettokraft auf unserer Fluiddomäne der Druck mal die Fläche am Ausgang minus der Druck mal die Fläche am Eingang.

Das Minuszeichen am Anfang dieses Ausdrucks wird verwendet, weil sich Gase von einem Bereich mit hohem Druck in einen Bereich mit niedrigem Druck bewegen. Ersetzen unserer Ausdrücke für Geschwindigkeitund Druck:

Vereinfachen:

Feststellend, dass (del x / del t) die Geschwindigkeit ist und dass die Masse die Dichte r mal das Volumen (Fläche mal del x) ist:

Vereinfachen:

Die del p / del x und del u / del xrepräsentieren die Druck- und Geschwindigkeitsgradienten.Wenn wir unsere Domäne auf differentielle Größen verkleinern, werden diese Gradienten zu Differentialen:

Dies ist eine eindimensionale, stetige Form Voneulers Equation.It es ist interessant festzustellen, dass der Druckabfall einer Flüssigkeit (der Begriff auf der linken Seite) proportional zum Wert der Geschwindigkeit und dem Gradienten der Geschwindigkeit ist.Eine Lösung dieser Impulsgleichung gibt uns die Form derdynamischer Druckdas erscheint Inbernoullis Gleichung.

Aktivitäten:
Führungen

• Grundlegende Fluiddynamikgleichungen:

Navigation ..

Anfängerleitfaden Startseite