Histogramme
Balkendiagramme, Häufigkeitsverteilungen und Histogramme
Häufigkeitsverteilungen, Balkendiagramme und Kreisdiagramme
Die Häufigkeit eines bestimmten Ereignisses gibt an, wie oft das Ereignis eintritt. Die relative Häufigkeit ist der Anteil der beobachteten Reaktionen in der Kategorie.
Beispiel: Wir haben die Schüler gefragt, aus welchem Land ihr Auto stammt (oder kein Auto) und die Antworten gezählt. Dann haben wir berechnetdie Häufigkeit und relative Häufigkeit jeder Kategorie. Die relative Frequenz wird berechnet, indem die Frequenz durch die Gesamtzahl der Befragten dividiert wird. The following tablesummarizes.
| Country | Frequency | Relative Frequency |
| US | 6 | 0.3 |
| Japan | 7 | 0.35 |
| Europe | 2 | 0.1 |
| Korea | 1 | 0.05 |
| None | 4 | 0.2 |
| Total | 20 | 1 |
Below is a bar graph for the car data. This bar graph is called a Paretochart since the height represents the frequency. Beachten Sie, dass die Breiten der Balken immer gleich sind.
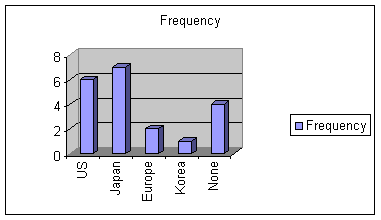
Wir machen ein Kreisdiagramm oftgenannt ein Kreisdiagramm dieser Daten durch Platzierenkeile im Kreis der proportionalen Größe zu den Frequenzen.
Unten ist ein Kreisdiagramm, das diese Daten anzeigt.
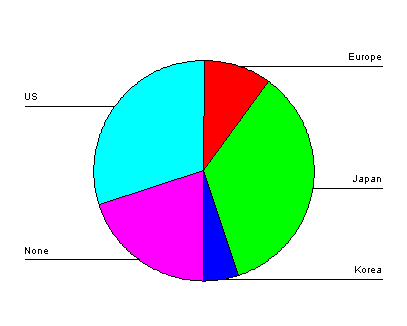
Um die Winkel der einzelnen Scheiben zu ermitteln, verwenden wir die Formel
Um beispielsweise den Winkel für US-Autos zu ermitteln, haben wir
6
Angle = x 360 = 108 Grad
20
Histogramme
Histogramme sind Balkendiagramme, deren vertikale Koordinate der Frequenzzählung entspricht und deren horizontale Koordinate zu einem numerischen Intervall.
Beispiel:
Die Tiefe der Klarheit des Lake Tahoe wurde an verschiedenen Stellen mit den Ergebnissen in Zoll wie folgt gemessen:
15.4, 16.7, 16.9, 17.0, 20.2, 25.3, 28.8, 29.1, 30.4, 34.5,
36.7, 39.1, 39.4, 39.6, 39.8, 40.1, 42.3, 43.5, 45.6, 45.9,
48.3, 48.5, 48.7, 49.0, 49.1, 49.3, 49.5, 50.1, 50.2, 52.3
We use a frequency distribution table with class intervals of length 5.
| Class Interval | Frequency | Relative Frequency | Cumulative Relative Frequency |
| <20 | 4 | 0.129 | 0.129 |
| <25 | 1 | 0.032 | 0.161 |
| < 30 | 3 | 0.097 | 0.258 |
| < 35 | 2 | 0.065 | 0.323 |
| < 40 | 6 | 0.194 | 0.516 |
| < 45 | 3 | 0.097 | 0.613 |
| < 50 | 9 | 0.290 | 0.903 |
| < 55 | 3 | 0.097 | 1.000 |
| Total | 31 | 1.000 |
Unten ist der Graph des Histogramms
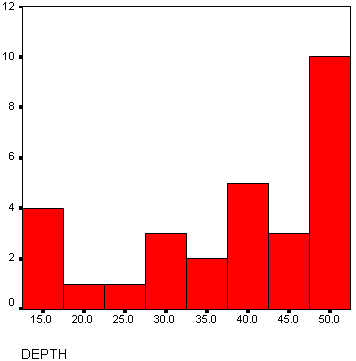
Die Form eines Histogramms
Ein Histogramm ist unimodal, wenn es eins gibthump, bimodal, wenn es zwei Höcker gibt und multimodal, wenn es viele Höcker gibt. Ein asymmetrisches Histogramm wird als schief bezeichnet, wenn es nicht symmetrisch ist. Ifthe oberen schwanz ist länger als die unteren schwanz dann es ist positivelyskewed. Wenn der obere Schwanz kürzer ist als negativ,gekürzt.
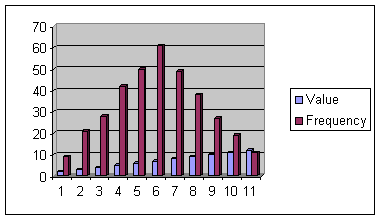Unimodal,Symmetric, Nonskewed
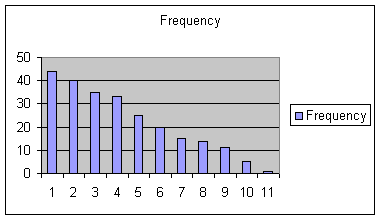Nonsymmetric,Skewed Right
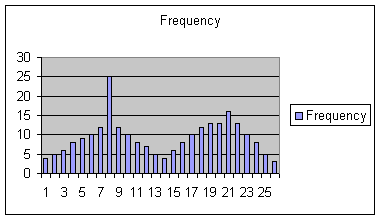Bimodal
Leave a Reply