In der klassischen Mechanikbearbeiten

In der nichtrelativistischen klassischen Mechanik ist ein geschlossenes System ein physikalisches System, das keine Materie mit seiner Umgebung austauscht und keiner Nettokraft unterliegt, deren Quelle außerhalb des Systems liegt. Ein geschlossenes System in der klassischen Mechanik würde einem isolierten System in der Thermodynamik entsprechen. Geschlossene Systeme werden häufig verwendet, um die Faktoren zu begrenzen, die die Ergebnisse eines bestimmten Problems oder Experiments beeinflussen können.

In der Thermodynamikbearbeiten

Eigenschaften isolierter, geschlossener und offener Systeme beim Austausch von Energie und Materie.

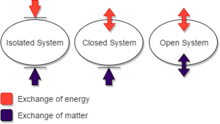
In der Thermodynamik kann ein geschlossenes System Energie (als Wärme oder Arbeit) austauschen, aber keine Materie, mit seiner surroundings.An ein isoliertes System kann keine Wärme, Arbeit oder Materie mit der Umgebung austauschen, während ein offenes System Energie und Materie austauschen kann. (Dieses Schema der Begriffsdefinition wird nicht einheitlich verwendet, obwohl es für einige Zwecke zweckmäßig ist. Insbesondere verwenden einige Autoren ein ‚geschlossenes System‘, wobei hier ein ‚isoliertes System‘ verwendet wird.)

Für ein einfaches System mit nur einem Partikeltyp (Atom oder Molekül) entspricht ein geschlossenes System einer konstanten Anzahl von Partikeln. Bei Systemen, die eine chemische Reaktion durchlaufen, können jedoch alle Arten von Molekülen durch den Reaktionsprozess erzeugt und zerstört werden. In diesem Fall wird die Tatsache, dass das System geschlossen ist, ausgedrückt, indem angegeben wird, dass die Gesamtzahl jedes elementaren Atoms konserviert ist, unabhängig davon, zu welcher Art von Molekül es gehört. Mathematisch:

∑ j = 1 m a i j N j = b i {\displaystyle \Summe _{j=1}^{m}a_{ij}N_{j}=b_{i}}

wobei N j {\displaystyle }}

ist die Anzahl der Moleküle vom j-Typ, a i j {\displaystyle a_{ij}}

ist die Anzahl der Atome des Elements i {\displaystyle i}

im Molekül j {\displaystyle j}

und b i {\displaystyle b_{i}}

ist die gesamtzahl der Atome des Elements i {\displaystyle i}

im System, die konstant bleibt, da das System geschlossen ist. Es wird eine solche Gleichung für jedes andere Element im System geben. In der Thermodynamik ist ein geschlossenes System wichtig, um komplizierte thermodynamische Probleme zu lösen. Es ermöglicht die Beseitigung einiger externer Faktoren, die die Ergebnisse des Experiments oder Problems verändern könnten, wodurch es vereinfacht wird. Ein geschlossenes System kann auch in Situationen verwendet werden, in denen ein thermodynamisches Gleichgewicht erforderlich ist, um die Situation zu vereinfachen.

In der Quantenphysik

Diese Gleichung, Schrödingers Gleichung genannt, beschreibt das Verhalten eines isolierten oder geschlossenen Quantensystems, dh definitionsgemäß eines Systems, das keine Informationen (dh Energie und / oder Materie) mit einem anderen System austauscht. Wenn sich also ein isoliertes System zum Zeitpunkt t in einem reinen Zustand | ψ(t) ∈ H befindet, wobei H den Hilbert-Raum des Systems bezeichnet, die zeitliche Entwicklung dieses Zustands (zwischen zwei aufeinanderfolgenden Messungen).

i ℏ ∂ ∂ t Ψ ( r , t ) = H ^ Ψ ( r , t ) {\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi \links(\mathbf {r} , t\rechts)={\hat {H}}\Psi \links(\mathbf {r} ,t\rechts)\,\!}