Fibonacci-Folge
Die Fibonacci-Folge ist die Zahlenreihe:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Die nächste Zahl wird gefunden, indem man die zwei Zahlen davor addiert:
- die 2 wird gefunden, indem man die zwei Zahlen davor addiert (1+1),
- die 3 wird gefunden, indem man die zwei Zahlen davor addiert (1+2),
- die 5 ist (2+3),
- und so weiter!
Beispiel: Die nächste Zahl in der obigen Sequenz ist 21+34 = 55
So einfach ist das!
Hier eine längere Liste:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Können Sie die nächsten Zahlen herausfinden?
Macht eine Spirale
Wenn wir Quadrate mit diesen Breiten machen, bekommen wir eine schöne Spirale:
Siehst du, wie die Quadrate ordentlich zusammenpassen?
Zum Beispiel 5 und 8 machen 13, 8 und 13 machen 21, und so weiter.

Diese Spirale kommt in der Natur vor!
Sehen: Natur, Der Goldene Schnitt und Fibonacci
Die Regel
Die Fibonacci-Folge kann als „Regel“ geschrieben werden (siehe Sequenzen und Reihen).
Zunächst werden die Begriffe ab 0 wie folgt nummeriert:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Der Begriff Nummer 6 heißt also x6 (was 8 entspricht).
|
Beispiel: Der 8. Term ist x8 = x7 + x6 |
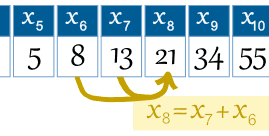 |
So können wir die Regel schreiben:
Die Regel ist xn = xn−1 + xn-2
wobei:
- xn ist Termnummer „n“
- xn−1 ist der vorherige Term (n−1)
- xn−2 ist der Term davor (n−2)
Beispiel: Term 9 wird folgendermaßen berechnet:
Goldener Schnitt
Und hier ist eine Überraschung. Wenn wir zwei aufeinanderfolgende (nacheinander) Fibonacci-Zahlen nehmen, liegt ihr Verhältnis sehr nahe am Goldenen Schnitt „φ“, der ungefähr 1,618034 beträgt…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
Wir müssen nicht mit 2 und 3 beginnen, hier habe ich zufällig 192 und 16 ausgewählt (und die Sequenz erhalten 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
Es dauert länger, um gute Werte zu erhalten, aber es zeigt, dass nicht nur die Fibonacci-Sequenz dies kann!
Verwendung des Goldenen Schnitts zur Berechnung von Fibonacci−Zahlen
Und noch überraschender ist, dass wir jede Fibonacci−Zahl mit dem Goldenen Schnitt berechnen können:
xn = φn – (1-φ)n√5
Die Antwort kommt als ganze Zahl heraus, genau gleich der Addition der beiden vorherigen Terme.
Beispiel: x6
x6 = (1.618034…)6 − (1−1.618034…)6√5
Als ich dazu einen Taschenrechner verwendete (nur den Goldenen Schnitt auf 6 Dezimalstellen eingab), erhielt ich die Antwort 8.00000033 , eine genauere Berechnung wäre näher an 8.
Versuchen Sie n=12 und sehen Sie, was Sie bekommen.
Sie können eine Fibonacci-Zahl auch berechnen, indem Sie die vorherige Fibonacci-Zahl mit dem Goldenen Schnitt multiplizieren und dann runden (funktioniert für Zahlen über 1):
Beispiel: 8 × φ = 8 × 1,618034… = 12.94427… = 13 (gerundet)
Einige interessante Dinge
Hier ist wieder die Fibonacci-Sequenz:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Es gibt ein interessantes Muster:
- Schau dir die Zahl x3 = 2 an. Jede 3. Zahl ist ein Vielfaches von 2 (2, 8, 34, 144, 610, …)
- Schau dir die Zahl x4 = 3 an. Jede 4. Zahl ist ein Vielfaches von 3 (3, 21, 144, …)
- Schau dir die Zahl x5 = 5 an. Jede 5. Zahl ist ein Vielfaches von 5 (5, 55, 610, …)
Und so weiter (jede n-te Zahl ist ein Vielfaches von xn).
1/89 = 0,011235955056179775…
Beachten Sie, dass die ersten Ziffern (0,1,1,2,3,5) die Fibonacci-Sequenz sind?
In gewisser Weise sind sie alle, außer dass sich mehrstellige Zahlen (13, 21 usw.) wie folgt überlappen:
… etc…
0,011235955056179775… = 1/89
Begriffe unter Null
Die Sequenz funktioniert auch unter Null wie folgt:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Beweisen Sie sich, dass jede Zahl gefunden wird, indem Sie die beiden Zahlen davor addieren!)
Tatsächlich hat die Sequenz unter Null die gleichen Zahlen wie die Sequenz über Null, außer dass sie einem +-+- folgen … Muster. Es kann so geschrieben werden:
x-n = (-1)n+1 xn
Was besagt, dass der Begriff „-n“ gleich (-1) n+ 1 mal dem Begriff „n“ ist, und der Wert (-1)n+1 macht ordentlich die richtige +1, -1, +1, -1, … Muster.
Geschichte
Fibonacci war nicht der erste, der von der Sequenz erfuhr, sie war Hunderte von Jahren zuvor in Indien bekannt!

Über Fibonacci Der Mann
Sein richtiger Name war Leonardo Pisano Bogollo, und er lebte zwischen 1170 und 1250 in Italien.
„Fibonacci“ war sein Spitzname, was ungefähr „Sohn von Bonacci“ bedeutet.
Er war nicht nur berühmt für die Fibonacci-Folge, sondern half auch, hindu-arabische Ziffern (wie unsere heutigen Zahlen) zu verbreiten 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) durch Europa anstelle von römischen Ziffern (I, II, III, IV, V usw.). Das hat uns allen viel Ärger erspart! Danke Leonardo.

Fibonacci-Tag
Der Fibonacci-Tag ist der 23. November, da er die Ziffern „1, 1, 2, 3“ hat, die Teil der Sequenz sind. Also weiter November 23 lass es alle wissen!


Leave a Reply