Ich habe immer „Permutation“ und „Kombination“ verwechselt — welche ist welche?

Hier ist eine einfache Möglichkeit, sich daran zu erinnern: Permutation klingt kompliziert, nicht wahr? Und das ist es. Bei Permutationen ist jedes kleine Detail wichtig. Alice, Bob und Charlie unterscheidet sich von Charlie, Bob und Alice (geben Sie hier die Namen Ihrer Freunde ein).

Kombinationen hingegen sind ziemlich einfach. Die Details spielen keine Rolle. Alice, Bob und Charlie ist das gleiche wie Charlie, Bob und Alice.

Permutationen sind für Listen (Reihenfolge ist wichtig) und Kombinationen sind für Gruppen (Reihenfolge spielt keine Rolle).Wissen Sie, ein „Kombinationsschloss“ sollte wirklich als „Permutationsschloss“ bezeichnet werden. Die Reihenfolge, in der Sie die Zahlen eingeben, ist wichtig.

Ein echtes „Zahlenschloss“ würde sowohl 10-17-23 als auch 23-17-10 als korrekt akzeptieren.

Permutationen: Die haarigen Details

Beginnen wir mit Permutationen oder allen möglichen Möglichkeiten, etwas zu tun. Wir verwenden den Fancy-Pants-Begriff „Permutation“, also werden wir uns um jedes Detail kümmern, einschließlich der Reihenfolge jedes Artikels. Angenommen, wir haben 8 Personen:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

Wie viele Möglichkeiten können wir unter acht Teilnehmern einen 1., 2. und 3. Platz vergeben? (Gold / Silber / Bronze)

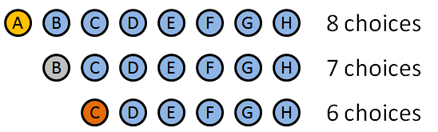
Wir werden Permutationen verwenden, da die Reihenfolge, in der wir diese Medaillen verteilen, von Bedeutung ist. Hier ist, wie es zusammenbricht:

• Goldmedaille: 8 Auswahlmöglichkeiten: A B C D E F G H (Clever, wie ich die Namen mit Buchstaben übereinstimmen ließ, eh?). Nehmen wir an, A gewinnt das Gold.
• Silbermedaille: 7 Auswahlmöglichkeiten: B C D E F G H. Nehmen wir an, B gewinnt das Silber.
• Bronzemedaille: 6 Möglichkeiten: C D E F G H. Sagen wir mal … C gewinnt Bronze.

Wir haben bestimmte Leute ausgewählt, um zu gewinnen, aber die Details spielen keine Rolle: Wir hatten zuerst 8 Entscheidungen, dann 7, dann 6. Die Gesamtzahl der Optionen war $8 * 7 * 6 = 336$.

Schauen wir uns die Details an. Wir mussten 3 von 8 Personen bestellen. Um dies zu tun, begannen wir mit allen Optionen (8) und nahmen sie dann einzeln weg (7, dann 6), bis uns die Medaillen ausgingen.

Wir wissen, dass die Fakultät:

Leider macht das zu viel! Wir wollen nur $8 * 7 * 6 $. Wie können wir die Fakultät bei 5 „stoppen“?

Hier werden Permutationen cool: Beachten Sie, wie wir sie loswerden wollen $5 * 4 * 3 * 2 * 1$. Was ist ein anderer Name dafür? 5 fakultät!

Also, wenn wir 8 machen!/5! wir erhalten:

Und warum haben wir die Zahl 5 verwendet? Weil es übrig blieb, nachdem wir 3 Medaillen von 8 ausgewählt hatten. Ein besserer Weg, dies zu schreiben, wäre also:

wobei 8!/(8-3)! ist nur eine ausgefallene Art zu sagen „Benutze die ersten 3 Zahlen von 8!”. Wenn wir insgesamt n Elemente haben und k in einer bestimmten Reihenfolge auswählen möchten, erhalten wir:

Und dies ist die ausgefallene Permutationsformel: Sie haben n Elemente und möchten die Anzahl der Möglichkeiten ermitteln, wie k Elemente bestellt werden können:

Kombinationen, Ho!

Kombinationen sind einfach. Ordnung spielt keine Rolle. Sie können es mischen und es sieht genauso aus. Nehmen wir an, ich bin ein Cheapskate und kann mir keine separaten Gold-, Silber- und Bronzemedaillen leisten. Tatsächlich kann ich mir nur leere Blechdosen leisten.

Wie viele Möglichkeiten kann ich 8 Personen 3 Blechdosen geben?

Nun, in diesem Fall spielt die Reihenfolge, in der wir die Leute auswählen, keine Rolle. Wenn ich Alice, Bob und dann Charlie eine Dose gebe, ist es dasselbe, als würde ich Charlie, Alice und dann Bob geben. So oder so, sie sind gleichermaßen enttäuscht.

Dies wirft einen interessanten Punkt auf – wir haben hier einige Redundanzen. Alice Bob Charlie = Charlie Bob Alice. Lassen Sie uns für einen Moment herausfinden, wie viele Möglichkeiten wir 3 Personen neu anordnen können.

Nun, wir haben 3 Möglichkeiten für die erste Person, 2 für die zweite und nur 1 für die letzte. Wir haben also $3 * 2 * 1 $ möglichkeiten, 3 Personen neu zu arrangieren.

Moment mal … das sieht ein bisschen aus wie eine Permutation! Du hast mich reingelegt!

Ja, das habe ich. Wenn Sie N Personen haben und wissen möchten, wie viele Arrangements es für alle gibt, ist es nur N Fakultät oder N!

Wenn wir also 3 Blechdosen zum Verschenken haben, sind es 3! oder 6 Variationen für jede Wahl, die wir wählen. Wenn wir herausfinden wollen, wie viele Kombinationen wir haben, erstellen wir einfach alle Permutationen und dividieren durch alle Redundanzen. In unserem Fall erhalten wir 336 Permutationen (von oben), und wir dividieren durch die 6 Redundanzen für jede Permutation und erhalten 336/6 = 56.

Die allgemeine Formel lautet

was bedeutet „Finde alle Möglichkeiten, k Personen aus n auszuwählen, und dividiere durch das k! Motorvarianten”. Wenn wir dies aufschreiben, erhalten wir unsere Kombinationsformel oder die Anzahl der Möglichkeiten, k Elemente aus einer Menge von n zu kombinieren:

Manchmal wird C(n,k) geschrieben als:

das ist der Binomialkoeffizient.

Ein paar Beispiele

Hier sind einige Beispiele für Kombinationen (Reihenfolge spielt keine Rolle) aus Permutationen (Reihenfolge ist wichtig).

• Kombination: Auswahl eines Teams von 3 Personen aus einer Gruppe von 10 Personen. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

  Permutation: Kommissionierung eines Präsidenten, VP und Waterboy aus einer Gruppe von 10. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.

• Kombination: Auswahl von 3 Desserts aus einem Menü von 10. C(10,3) = 120.

  Permutation: Auflistung Ihrer 3 Lieblings-Desserts, um aus einem Menü von 10. P(10,3) = 720.

Merken Sie sich die Formeln nicht, verstehen Sie, warum sie funktionieren. Kombinationen klingen einfacher als Permutationen, und das sind sie auch. Sie haben weniger Kombinationen als Permutationen.

Weitere Beiträge in dieser Serie

1. Einfache Permutationen und Kombinationen
2. Navigieren Sie in einem Raster mit Kombinationen und Permutationen
3. Wie man Kombinationen mit Multiplikation versteht
4. Warum multiplizieren wir Kombinationen?