Eine Kraft kann als Stoß oder Zug in eine bestimmte Richtung betrachtet werden. Wenn eine Kraft auf ein Objekt ausgeübt wird, hängt die resultierende Bewegung des Objekts davon ab, wo die Kraft ausgeübt wird und wie das Objekt begrenzt ist.Wenn das Objekt nicht begrenzt ist und die Kraft durch den Schwerpunkt ausgeübt wird, bewegt sich das Objekt in reiner Übersetzung, wie durch Newtons Bewegungsgesetze beschrieben.Wenn sich das Objekt an einer Stelle namens apivot befindet (oder angeheftet ist), gibt das objectrotatesabout den Drehpunkt an, wird jedoch nicht übersetzt.Die Kraft wird durch den Drehpunkt übertragenund die Details der Drehung hängen von der Entfernung abdie aufgebrachte Kraft auf den Drehpunkt.Wenn das Objekt nicht begrenzt ist und die Kraft in einiger Entfernung vom Schwerpunkt ausgeübt wird, das Objekt beide translatesand dreht sich um den Schwerpunkt.Die Details der Rotation hängen von der Entfernung von derangewandte Kraft zum Schwerpunkt.Die Bewegung von Flugobjekten wird durch diese dritte Art von Bewegung beschrieben; eine Kombination aus Translation und Rotation.

Eine Kraft F ist eine Vektorgröße,was bedeutet, dass ihr sowohl eine Größe als auch eine Richtung zugeordnet sind. Dierichtung der forceis wichtig, weil die resultierende Bewegung des objectis in der gleichen Richtung wie die Kraft.Das Produkt aus der Kraft und dem senkrechten Abstand zum Schwerpunkt für ein nicht begrenztes Objekt oder zum Drehpunkt für ein begrenztes Objekt wird als Drehmoment oder Moment bezeichnet.Ein Drehmoment ist auch eine Vektorgröße und erzeugt eine rotationin der gleichen Weise, dass eine Kraft eine Übersetzung erzeugt. Ein Objekt, das sich in Ruhe befindet oder mit einer konstanten Winkelgeschwindigkeit rotiert, wird dies so lange tun, bis es einem externen Drehmoment ausgesetzt ist. Ein Drehmoment erzeugt eine Änderung der Winkelgeschwindigkeit, die als Winkelbeschleunigung bezeichnet wird.

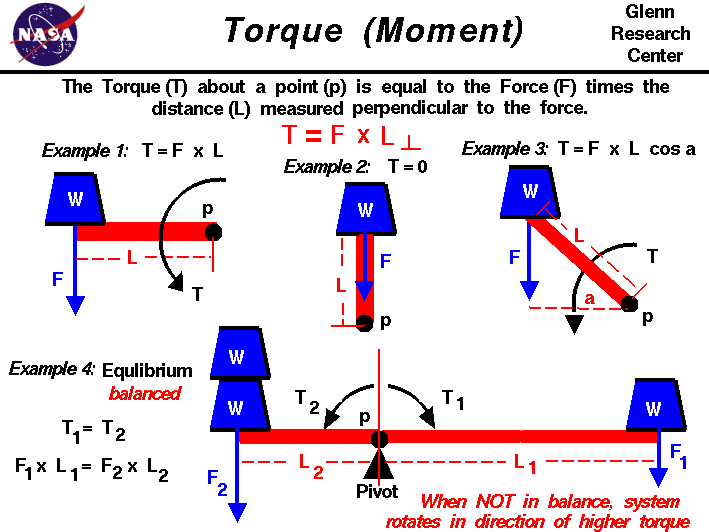
Der Abstand L, der verwendet wird, um das Drehmoment T zu bestimmen, ist der Abstand von thepivot p zur Kraft, aber gemessen senkrecht zu thedirection der Kraft.In der Abbildung zeigen wir vier Beispiele für Drehmomente, um die Grundlagen zu veranschaulichenprinzipien . torques.In in jedem Beispiel wirkt ein blaues Gewicht W auf einen roten Balken, der als Arm bezeichnet wird.

In Beispiel 1 wird die Kraft (Gewicht) senkrecht auf den Arm aufgebracht. In diesem Fall ist der senkrechte Abstand die Länge der Stange und das Drehmoment ist gleich dem Produkt aus Länge und Kraft.

In Beispiel 2 wird die gleiche Kraft auf den Arm ausgeübt, aber die Kraft wirkt jetzt direkt durch diepivot. In diesem Fall ist der Abstand vom Drehpunkt senkrecht zur Kraftist Null. In diesem Fall ist also auch das Drehmoment Null.Denken Sie an eine Drehtür. Wenn sie push-onthe rand der tür, in richtung der scharnier, die tür nicht movebecause die drehmoment ist null.

Beispiel 3 ist der allgemeine Fall, in dem die Kraft in einem Winkel a auf den Arm ausgeübt wird. Der senkrechte Abstand ist gegeben Durchtrigonometrie als die Länge des Arms (L) mal Derkosinus (cos)des Winkels.Das Drehmoment ist dann gegeben durch:

Die Beispiele 1 und 2 können aus dieser allgemeinen Formel abgeleitet werden, da der Kosinus von0 Grad ist 1,0 (Beispiel 1) und der Kosinus von 90 Grad ist 0,0 (Beispiel 2).

In Beispiel 4 wurde der Drehpunkt vom Ende der Stange zu einer Position nahe der Mitte der Stange bewegt. Gewichte werden zu beiden sidesof addiert pivot.To rechts erzeugt ein einzelnes Gewicht W eine Kraft F1, die in einem Abstand L1 vom Drehpunkt wirkt. Dies erzeugt ein Drehmoment T1 gleich derProdukt der Kraft und des Abstandes.

Links vom Pivot erzeugen zwei Gewichte W eine Kraft F2 in einem Abstand L2.Dieses producesa Drehmoment T2 in einer Richtung entgegengesetzt zu T1, weil der distanceis in der entgegengesetzten Richtung.

Wenn das System im Gleichgewicht oder ausgeglichen wäre, wären die Drehmomente gleich und es würde kein Nettomoment auf das System einwirken.

Wenn sich das System nicht im Gleichgewicht oder unausgeglichen befindet, dreht sich der Stabum den Drehpunkt in Richtung des höheren Drehmoments.Wenn F2 = 2 * F1, wie ist die Beziehung zwischen L1 und L2, um das System auszugleichen? Wenn F2 = 2 * F1 und L1 = L2, in welche Richtung würde sich das System drehen?

Luftfahrtingenieure nutzen das von aerodynamischen Oberflächen erzeugte Drehmoment,um Flugzeuge zu stabilisieren und zu steuern.In Flugzeugen erzeugen die Steuerflächen.aerodynamische Kräfte.Diese Kräfte werden in einiger Entfernung vom Flugzeug aufgebracht und bewirken daher, dass sich das Flugzeug dreht. Theelevators produzieren apitching moment, therudder produzieren ayawing moment, und theailerons produzieren arolling moment. Die Fähigkeit, die Kraft und den Moment zu variieren, ermöglicht es dem Piloten, das Flugzeug zu manövrieren oder zu trimmen.Auf Modellraketen, thefins werden verwendet, um ein Drehmoment über die rocketcenter der gravityto providestabilityduring Motorflug zu erzeugen.Auf drachen, die aerodynamische und gewicht forcesproduce ein drehmoment über thebridle punkt.Die entfernung von der zaum punkt und die größe der kräfte hat eine starke wirkung auf die leistung der kite.

Aktivitäten:
Führungen

• Kräfte, Drehmomente und Bewegung:
• Grundlegende:
• Rollbewegung des Flugzeugs:
• 
• Flugzeuggierbewegung:
• Querruder:
• Spoiler:
• Id:
• 
• Ruder:
• Stabilität einer Modellrakete:

Navigation..

Startseite des Anfängerleitfadens