Die schönsten und wichtigsten mathematischen Gleichungen
Mathematik ist eher ein Marathon als ein Sprint — es ist ein langer, langsamer und stetiger Grind mit seltenen Momenten des Durchbruchs. Immer noch, ab und zu, Wir bekommen diese wertvollen „Eureka“ -Momente, diese kurzen Zeilen mit Buchstaben und Zahlen, die die Wissenschaft für immer verändern. Hier sind einige der berühmtesten Gleichungen, von den alten Griechen bis zur modernen Physik.
Satz von Pythagora (530 v. Chr.)
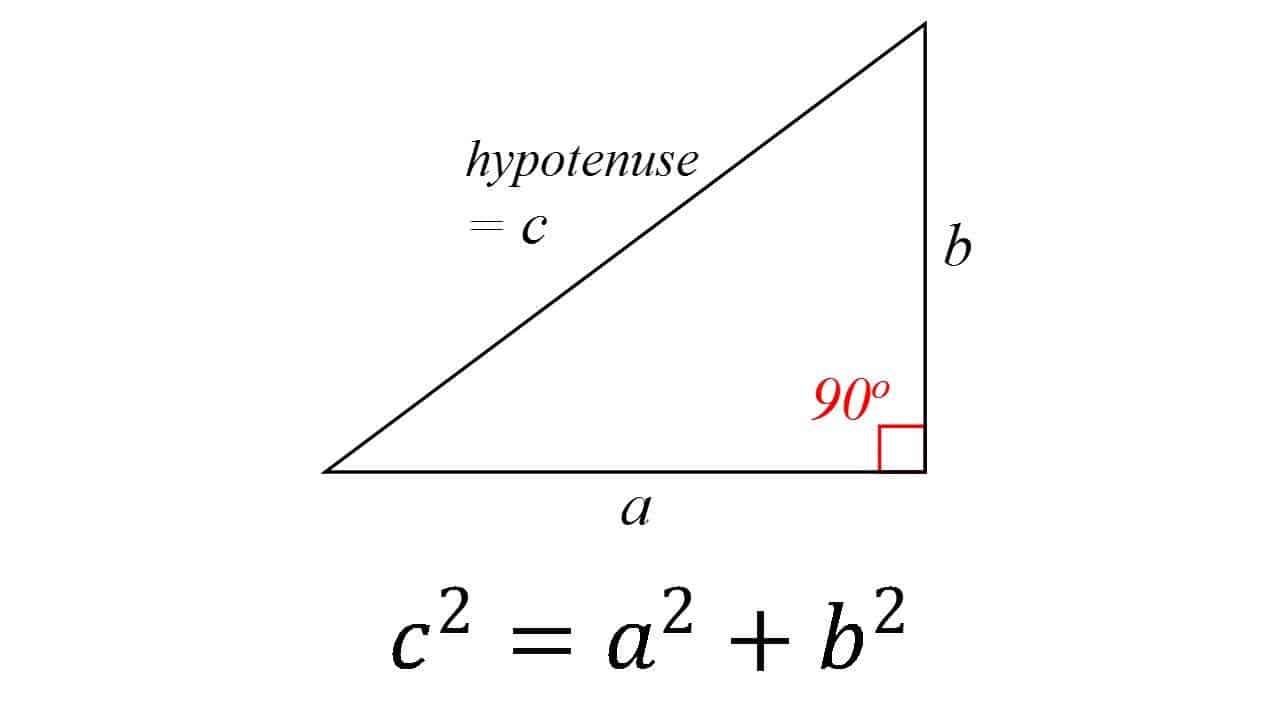
Dies ist ziemlich eine der grundlegenden Säulen aller Geometrie: in einem rechtwinkligen Dreieck ist das Quadrat der Hypotenuse (die dem rechten Winkel gegenüberliegende Seite) gleich der Summe der Quadrate der beiden anderen. Die Theorie wird im Allgemeinen dem griechischen Mathematiker Pythagoras zugeschrieben, obwohl es einige Hinweise darauf gibt, dass babylonische Mathematiker die Formel verstanden haben. Es ist auch sehr gut möglich, dass der Satz vielen Menschen bekannt war, aber er war der erste, der es bewies.
Der Satz hat zahlreiche Beweise erhalten – möglicherweise die meisten für jeden mathematischen Satz. Sie sind sehr vielfältig, einschließlich geometrischer Beweise und algebraischer Beweise, mit einigen Dating Tausende von Jahren zurück.
Komplexe Zahlen

Der italienische Mathematiker Gerolamo Cardano ist der erste bekannte, der komplexe Zahlen eingeführt und sie damals als „fiktiv“ bezeichnet hat. Die mathematische Entwicklung von „i“ als imaginäre Zahl, die die Quadratwurzel von -1 darstellt, wird jedoch Leonhard Euler zugeschrieben, einem der wichtigsten Mathematiker und Wissenschaftler der Menschheitsgeschichte.
Komplexe Zahlen sind im Grunde Zahlen, die nicht wirklich existieren, aber für eine Reihe von Berechnungen sehr nützlich sind. Sie bestehen aus Zahlen mit einem Realteil (die Zahlen, die wir alle kennen) und einem Imaginärteil (die ich hier dargestellt habe) und haben praktische Anwendungen in vielen Bereichen, einschließlich Physik, Chemie, Biologie, Wirtschaft, Elektrotechnik und Statistik.
Die Logarithmen

Logarithmen sind grundsätzlich die inverse Funktion der Potenzierung. Sie benötigen eine Zahl (N), eine Basis (a), und der Logarithmus von N in Basis a ist x, wobei N a der Potenz von x . Es mag nur eine andere Art zu sein scheinen, dasselbe zu schreiben (und in gewissem Sinne ist es das), aber Logarithmen haben eine Vielzahl praktischer Anwendungen und werden in der Psychologie, Wirtschaft und Messung vieler physikalischer Phänomene (wie pH-Wert oder Erdbebengröße) verwendet.Logarithmen wurden 1614 von John Napier in einem Buch mit dem Titel Mirifici Logarithmorum Canonis Descriptio (Beschreibung der wunderbaren Regel der Logarithmen) öffentlich vorgestellt — ein passender Titel. Ein Sonderfall des Logarithmus ist der natürliche Logarithmus – e, wobei e eine irrationale und transzendentale Zahl ist, die ungefähr 2,71828182845 entspricht. Tatsächlich hat e selbst eine faszinierende Geschichte und eine beeindruckende Anzahl von Anwendungen, aber das ist eine Geschichte für eine andere Zeit.
Kalkül
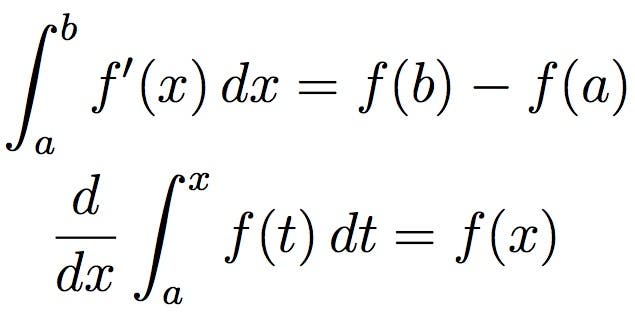
Nur wenige Bereiche der Mathematik waren so wirkungsvoll wie Kalkül. Entwickelt im 17.Jahrhundert von Isaac Newton und Gottfried Wilhelm Leibniz, ist Kalkül in Wissenschaft, Technik und Wirtschaft weit verbreitet. Kalkül konzentriert sich normalerweise auf den Umgang mit kleinen Mengen, insbesondere unendlich kleinen Mengen. Durch Kalkül können diese als reelle Zahlen behandelt werden, obwohl sie technisch unendlich klein sind.
Für eine einfachere Visualisierung kann die Integration, wie oben dargestellt, als Messung der Fläche unter einer Kurve betrachtet werden, die durch eine Funktion definiert ist.
Das Gesetz der Schwerkraft
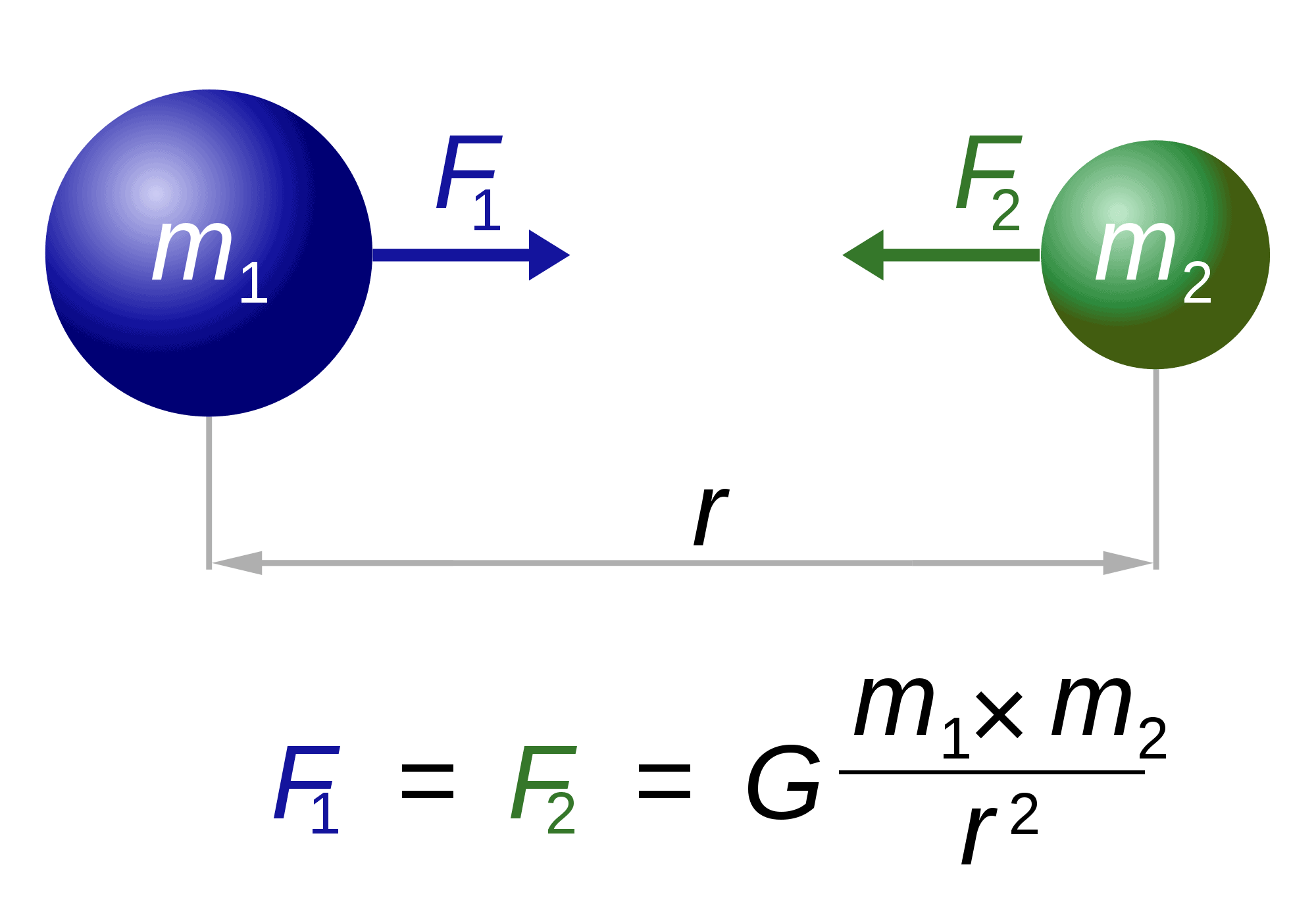
Apropos Newton, er ist auch „verantwortlich“ für eine der berühmtesten und spektakulärsten Gleichungen der Welt: das Gesetz der Schwerkraft.
Das Gesetz beschreibt grundsätzlich, wie zwei beliebige Massenkörper m1 und m2 zueinander hingezogen werden. Die Kraft (F1, F2) ist umgekehrt proportional zum Quadrat des Abstands zwischen ihnen (r). Der einzige verbleibende Faktor, G, ist eine Gravitationskonstante. Die Natur dieser Konstante bleibt schwer fassbar.
Allgemeine Relativitätstheorie

Seit fast 200 Jahren definiert das Newtonsche Gesetz unser Verständnis der Mechanik. Einsteins Arbeit im 20.Jahrhundert brachte die Dinge auf die nächste Stufe — diese beiden Errungenschaften ragen auf den höchsten Sockeln der Welt der Physik empor.Die Allgemeine Relativitätstheorie ist im Wesentlichen eine geometrische Gravitationstheorie, die Newtons Theorie verallgemeinert und eine einheitliche Beschreibung der Schwerkraft als geometrische Eigenschaft von Raum und Zeit — oder Raumzeit – liefert. Insbesondere zeigte Einstein nicht nur, dass es so etwas wie „Raumzeit“ gibt, die die drei Dimensionen mit der 4. Dimension der Zeit verschmilzt, sondern er zeigte auch, dass diese Raumzeit durch die Schwerkraft gekrümmt werden kann, wobei die Krümmung direkt mit der Energie und dem Impuls von Materie und Strahlung zusammenhängt.
Zweiter Hauptsatz der Thermodynamik
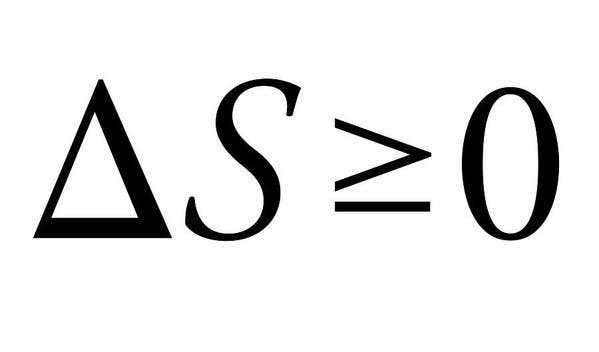
Der zweite Hauptsatz der Thermodynamik ist, warum wir keine schönen Dinge im Universum haben können. Scherze beiseite, die vier Gesetze der Thermodynamik definieren grundlegende physikalische Größen (Temperatur, Energie und Entropie), die thermodynamische Systeme charakterisieren. Insbesondere der zweite zeichnet sich hier durch seine Einfachheit, aber absolut massive Implikationen aus.Das Gesetz besagt im Wesentlichen, dass die Summe der Entropien der wechselwirkenden thermodynamischen Systeme immer zunehmen oder höchstens konstant bleiben muss. Wenn sich Energie von einer Form in eine andere ändert oder sich Materie bewegt, nimmt die Entropie (oder Unordnung) in einem geschlossenen System zu. Alle Unterschiede in Temperatur, Druck und Dichte neigen dazu, nach einer Weile flach zu werden
Maxwells Gleichungen
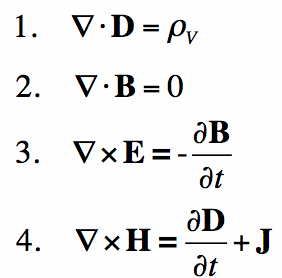
Einfach gesagt, Maxwells Gleichungen sind für den Elektromagnetismus das, was Newtons Gesetz für die Mechanik ist. Sie bieten eine mathematische Grundlage für klassischen Elektromagnetismus, klassische Optik und elektrische Schaltungen. Sie sind weit verbreitet in dem Gerät, auf dem Sie dies lesen — im Grunde alle elektronischen Geräte.Maxwells Gesetze beschreiben, wie elektrische und magnetische Felder durch Ladungen, Ströme und Änderungen der Felder erzeugt werden. Ein bedeutender Durchbruch war die Demonstration, dass sich elektrische und magnetische Felder mit Lichtgeschwindigkeit ausbreiten.
Eulers Identität

Schließlich ist dies möglicherweise die eleganteste Gleichung, eine Sache von höchster Schönheit, weil sie alle „grundlegenden“ Zahlen beinhaltet:
- 0, was für Addition und Subtraktion neutral ist;
- 1, was für Multiplikation und Division neutral ist;
- e, was die Zahl (siehe oben), die Basis der natürlichen Logarithmen;
- i ist die imaginäre Einheit (siehe oben); und
- π ist pi, das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
Eine Beziehung zu finden, die all diese Zahlen vereint, ist einfach atemberaubend und scheint ziemlich unwahrscheinlich. Die Demonstration ist nicht gerade einfach, aber Sie können es hier sehen.Es ist nur passend, dass der Mathematikprofessor der Stanford University, Keith Devlin, die Gleichung beschrieb und sagte: „Wie ein Shakespeare—Sonett, das die Essenz der Liebe einfängt, oder ein Gemälde, das die Schönheit der menschlichen Form hervorhebt, die weit mehr als nur hauttief ist, reicht Eulers Gleichung bis in die Tiefen der Existenz.“Es kommt nicht oft vor, dass Mathematik und Physik auf einfache und elegante Gleichungen hinauslaufen – aber wenn sie es tun, ist es ein unvergesslicher Anblick.
Leave a Reply