Einführung

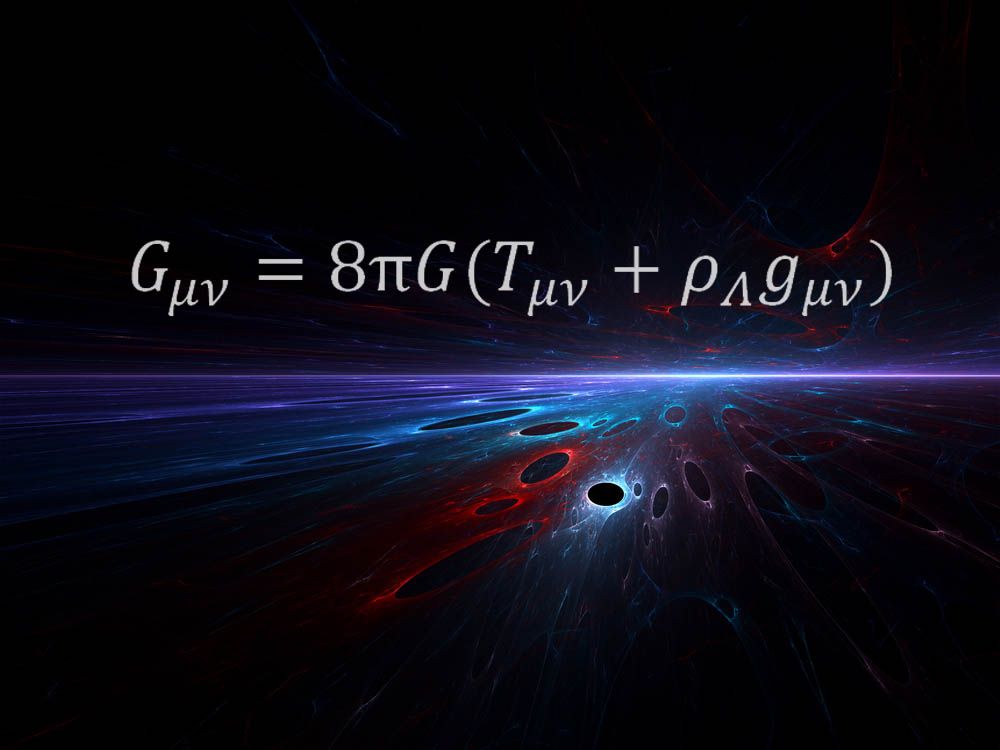
Mathematische Gleichungen sind nicht nur nützlich — viele sind ziemlich schön. Und viele Wissenschaftler geben zu, dass sie bestimmte Formeln nicht nur wegen ihrer Funktion, sondern auch wegen ihrer Form und der einfachen, poetischen Wahrheiten, die sie enthalten, lieben.Während bestimmte berühmte Gleichungen, wie Albert Einsteins E = mc ^ 2, den größten Teil des öffentlichen Ruhms in Anspruch nehmen, haben viele weniger bekannte Formeln ihre Champions unter Wissenschaftlern. LiveScience hat Physiker, Astronomen und Mathematiker nach ihren Lieblingsgleichungen gefragt; Folgendes haben wir gefunden:

Allgemeine Relativitätstheorie

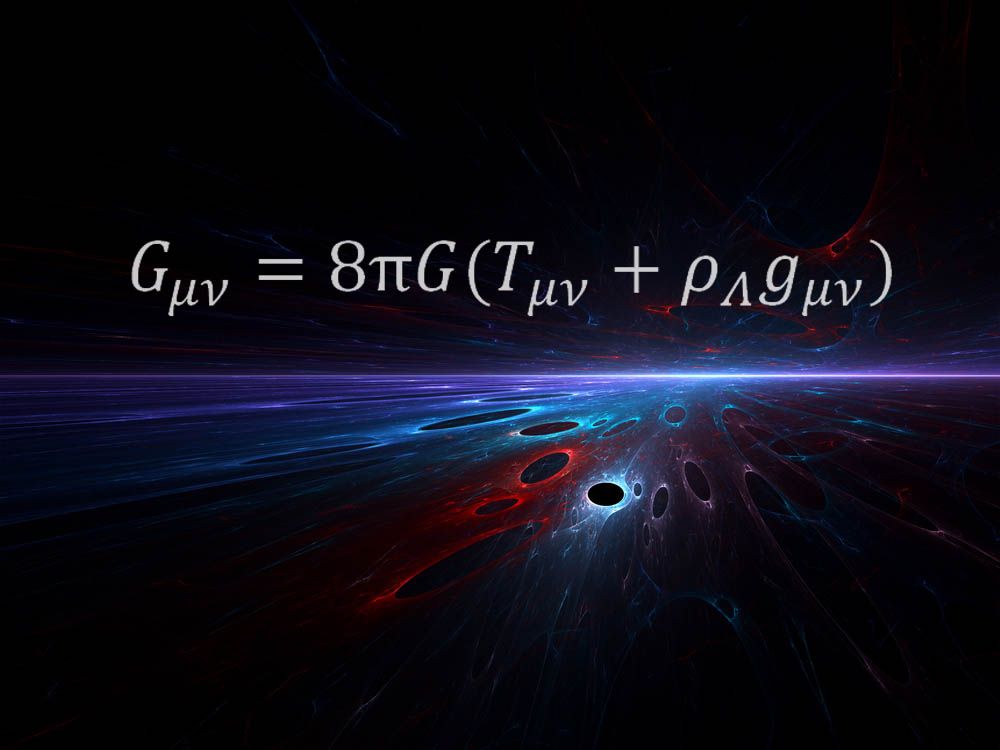
Die obige Gleichung wurde 1915 von Einstein als Teil seiner bahnbrechenden allgemeinen Relativitätstheorie formuliert. Die Theorie revolutionierte, wie Wissenschaftler die Schwerkraft verstanden, indem sie die Kraft als eine Verzerrung des Gewebes von Raum und Zeit beschrieben.“Es ist immer noch erstaunlich für mich, dass eine solche mathematische Gleichung beschreiben kann, worum es bei der Raumzeit geht“, sagte der Astrophysiker Mario Livio vom Space Telescope Science Institute, der die Gleichung als seinen Favoriten nominierte. „Das ganze wahre Genie Einsteins ist in dieser Gleichung verkörpert.“Die rechte Seite dieser Gleichung beschreibt den Energieinhalt unseres Universums (einschließlich der’dunklen Energie‘, die die aktuelle kosmische Beschleunigung antreibt)“, erklärte Livio. „Die linke Seite beschreibt die Geometrie der Raumzeit. Die Gleichheit spiegelt die Tatsache wider, dass in Einsteins allgemeiner Relativitätstheorie Masse und Energie die Geometrie und damit die Krümmung bestimmen, die eine Manifestation dessen ist, was wir Schwerkraft nennen.“Es ist eine sehr elegante Gleichung“, sagte Kyle Cranmer, Physiker an der New York University, und fügte hinzu, dass die Gleichung die Beziehung zwischen Raumzeit und Materie und Energie aufdeckt. „Diese Gleichung sagt Ihnen, wie sie zusammenhängen – wie die Anwesenheit der Sonne die Raumzeit verzerrt, so dass sich die Erde im Orbit um sie herum bewegt usw. Es sagt Ihnen auch, wie sich das Universum seit dem Urknall entwickelt hat und sagt voraus, dass es Schwarze Löcher geben sollte.“

Das Standardmodell

Das Standardmodell, eine weitere der vorherrschenden Theorien der Physik, beschreibt die Sammlung fundamentaler Teilchen, von denen derzeit angenommen wird, dass sie unser Universum bilden.Die Theorie kann in einer Hauptgleichung namens Standard Model Lagrange (benannt nach dem französischen Mathematiker und Astronomen Joseph Louis Lagrange aus dem 18.Jahrhundert) zusammengefasst werden, die vom theoretischen Physiker Lance Dixon vom SLAC National Accelerator Laboratory in Kalifornien als seine Lieblingsformel ausgewählt wurde.“Es hat erfolgreich alle Elementarteilchen und Kräfte beschrieben, die wir bisher im Labor beobachtet haben — außer der Schwerkraft“, sagte Dixon gegenüber LiveScience. „Dazu gehört natürlich das kürzlich entdeckte Higgs-Boson, phi in der Formel. Es ist völlig selbstkonsistent mit der Quantenmechanik und der speziellen Relativitätstheorie.“Die Standardmodelltheorie ist jedoch noch nicht mit der allgemeinen Relativitätstheorie vereinigt, weshalb sie die Gravitation nicht beschreiben kann.

Kalkül

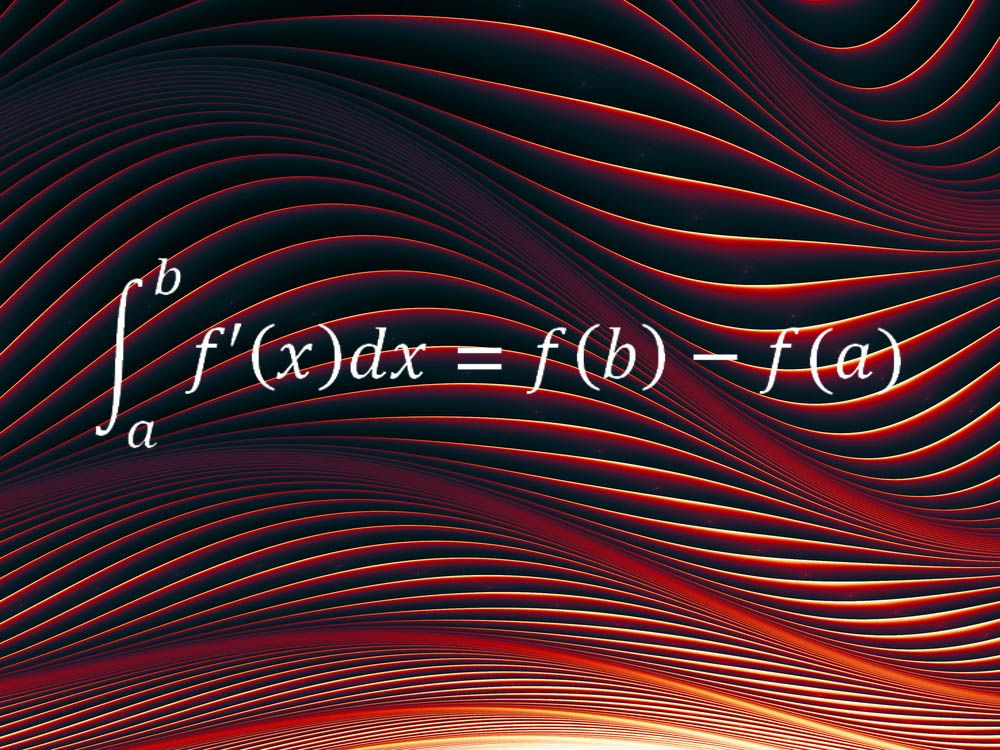
Während die ersten beiden Gleichungen bestimmte Aspekte unseres Universums beschreiben, kann eine andere Lieblingsgleichung auf alle möglichen Situationen angewendet werden. Der Fundamentalsatz der Infinitesimalrechnung bildet das Rückgrat der als Infinitesimalrechnung bekannten mathematischen Methode und verbindet ihre beiden Hauptideen, das Konzept des Integrals und das Konzept der Ableitung.

„In einfachen Worten, sagt, dass die Nettoänderung einer glatten und kontinuierlichen Größe, wie eine zurückgelegte Strecke, über ein gegebenes Zeitintervall (d.h. der Unterschied in den Werten der Größe an den Endpunkten des Zeitintervalls) ist gleich dem Integral der Änderungsrate dieser Größe, d. H. Dem Integral der Geschwindigkeit „, sagte Melkana Brakalova-Trevithick, Vorsitzende der mathematischen Abteilung an der Fordham University, die diese Gleichung als ihren Favoriten wählte. „Der Fundamentalsatz der Infinitesimalrechnung (FTC) ermöglicht es uns, die Nettoänderung über ein Intervall basierend auf der Änderungsrate über das gesamte Intervall zu bestimmen.“Die Saat des Kalküls begann in der Antike, aber ein Großteil davon wurde im 17.Jahrhundert von Isaac Newton zusammengestellt, der den Kalkül verwendete, um die Bewegungen der Planeten um die Sonne zu beschreiben.

Satz des Pythagoras

Eine „Oldie but Goodie“ -Gleichung ist der berühmte Satz des Pythagoras, den jeder beginnende Geometriestudent lernt.

Diese Formel beschreibt, wie für jedes rechtwinklige Dreieck das Quadrat der Länge der Hypotenuse c (die längste Seite eines rechtwinkligen Dreiecks) der Summe der Quadrate der Längen der anderen beiden Seiten (a und b) entspricht. So ist a ^ 2 + b ^ 2 = c ^ 2

„Die allererste mathematische Tatsache, die mich erstaunte, war der Satz des Pythagoras“, sagte die Mathematikerin Daina Taimina von der Cornell University. „Ich war damals ein Kind und es schien mir so erstaunlich, dass es in der Geometrie funktioniert und es funktioniert mit Zahlen!“

1 = 0,9999999999….

Diese einfache Gleichung, die besagt, dass die Menge 0,999, gefolgt von einer unendlichen Folge von Neunen, gleich eins ist, ist die favorit des Mathematikers Steven Strogatz von der Cornell University.“Ich liebe es, wie einfach es ist — jeder versteht, was es sagt — und doch wie provokativ es ist“, sagte Strogatz. „Viele Leute glauben nicht, dass es wahr sein könnte. Es ist auch schön ausgewogen. Die linke Seite repräsentiert den Beginn der Mathematik; die rechte Seite repräsentiert die Geheimnisse der Unendlichkeit.“

Spezielle Relativitätstheorie

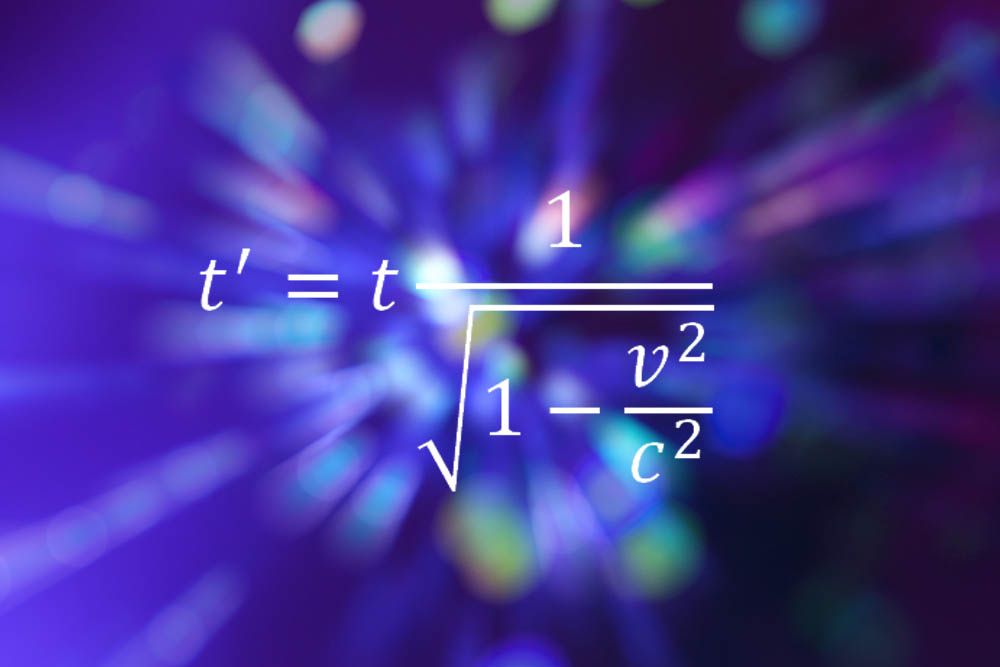
Einstein macht die Liste wieder mit seinen Formeln für die spezielle Relativitätstheorie, die beschreibt, wie Zeit und Raum keine absoluten Konzepte sind , sondern sind relativ in Abhängigkeit von der Geschwindigkeit des Beobachters. Die obige Gleichung zeigt, wie sich die Zeit ausdehnt oder verlangsamt, je schneller sich eine Person in eine beliebige Richtung bewegt.“Der Punkt ist, dass es wirklich sehr einfach ist“, sagte Bill Murray, ein Teilchenphysiker am CERN-Labor in Genf. „Es gibt nichts, was ein Abiturient nicht tun kann, keine komplexen Ableitungen und Spurenalgebren. Aber was es verkörpert, ist eine ganz neue Sichtweise auf die Welt, eine ganze Einstellung zur Realität und unsere Beziehung dazu. Plötzlich wird der starre unveränderliche Kosmos weggefegt und durch eine persönliche Welt ersetzt, die sich auf das bezieht, was Sie beobachten. Sie bewegen sich von außerhalb des Universums und schauen nach unten zu einer der Komponenten darin. Aber die Konzepte und die Mathematik können von jedem verstanden werden, der will.“Murray sagte, er ziehe die speziellen Relativitätsgleichungen den komplizierteren Formeln in Einsteins späterer Theorie vor. „Ich könnte niemals der Mathematik der allgemeinen Relativitätstheorie folgen“, sagte er.

Eulersche Gleichung

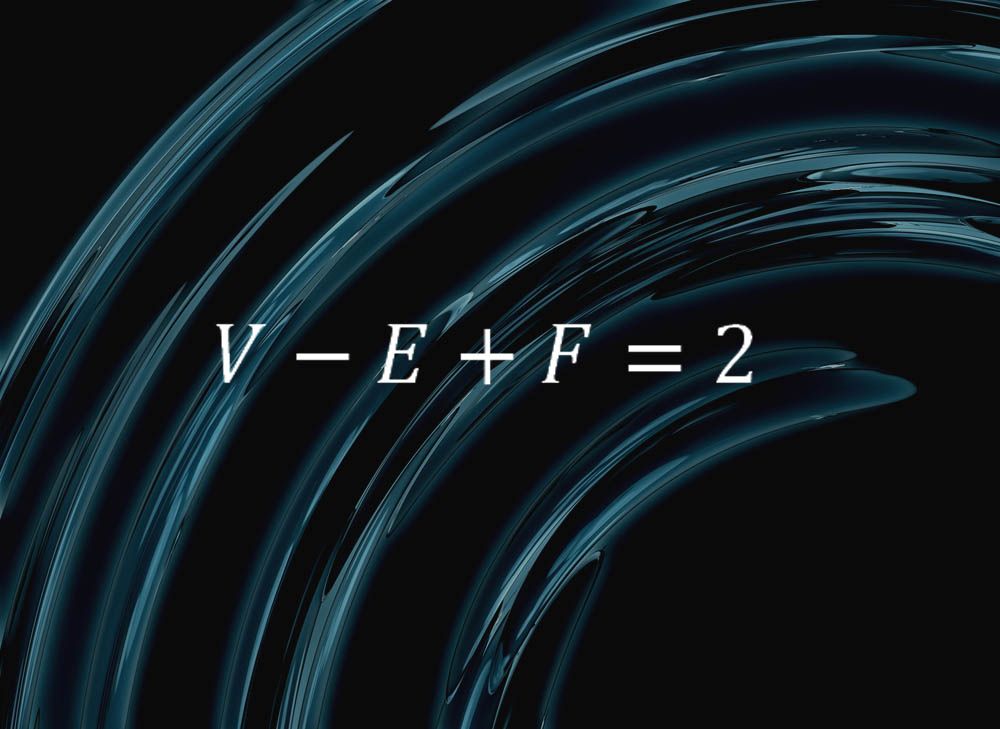
Diese einfache Formel kapselt etwas Reines über die Natur von Sphären ein:“Wenn man die Oberfläche einer Kugel in Flächen, Kanten und Eckpunkte schneidet und F die Anzahl der Flächen, E die Anzahl der Kanten und V die Anzahl der Eckpunkte ist, erhält man immer V – E + F = 2″, sagte Colin Adams, Mathematiker am Williams College in Massachusetts.“Nehmen wir zum Beispiel ein Tetraeder, das aus vier Dreiecken, sechs Kanten und vier Eckpunkten besteht“, erklärte Adams. „Wenn Sie hart in ein Tetraeder mit flexiblen Flächen bliesen, könnten Sie es zu einer Kugel abrunden, in diesem Sinne kann eine Kugel in vier Flächen, sechs Kanten und vier Eckpunkte geschnitten werden. Und wir sehen, dass V – E + F = 2. Gleiches gilt für eine Pyramide mit fünf Flächen — vier dreieckige und ein Quadrat — acht Kanten und fünf Ecken,“und jede andere Kombination von Flächen, Kanten und Ecken.

„Eine sehr coole Tatsache! Die Kombinatorik der Ecken, Kanten und Flächen erfasst etwas sehr Grundlegendes an der Form einer Kugel „, sagte Adams.

Euler-Lagrange-Gleichungen und Noether-Theorem

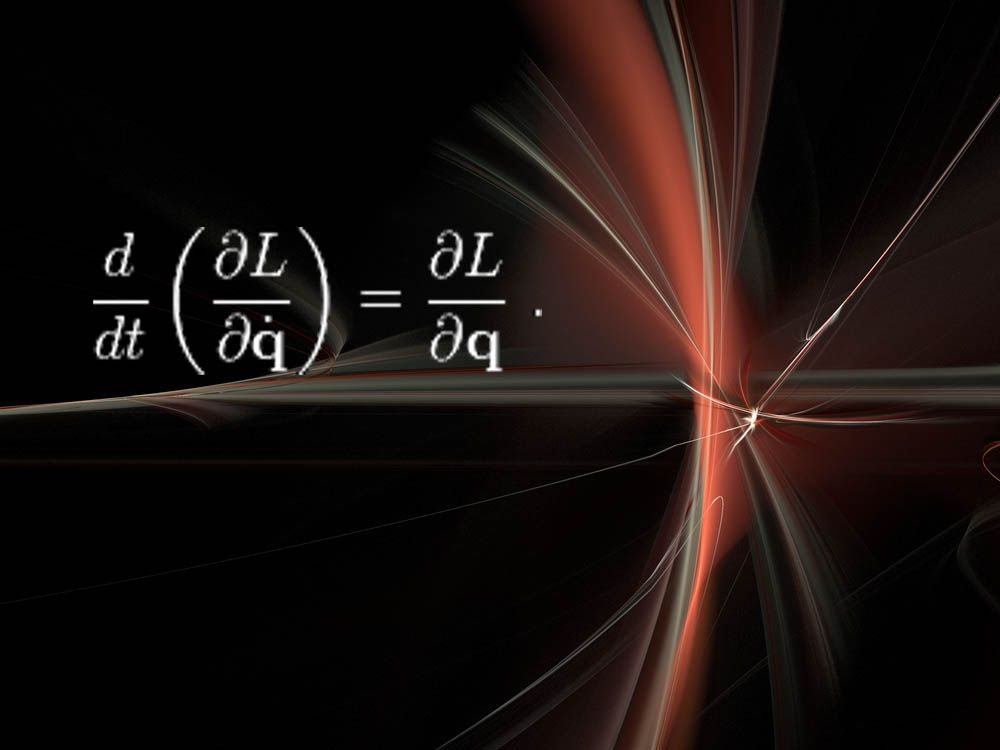
„Diese sind ziemlich abstrakt, aber erstaunlich mächtig“, sagte Cranmer von der NYU. „Das Coole ist, dass diese Art, über Physik nachzudenken, einige große Revolutionen in der Physik überlebt hat, wie Quantenmechanik, Relativitätstheorie usw.“

Hier steht L für den Lagrange-Wert, der ein Maß für die Energie in einem physikalischen System wie Federn oder Hebeln oder fundamentalen Teilchen ist. „Wenn Sie diese Gleichung lösen, erfahren Sie, wie sich das System mit der Zeit entwickeln wird“, sagte Cranmer.Ein Spin-off der Lagrange-Gleichung heißt Noether’s Theorem, nach der deutschen Mathematikerin Emmy Noether aus dem 20.Jahrhundert. „Dieser Satz ist wirklich grundlegend für die Physik und die Rolle der Symmetrie“, sagte Cranmer. „Informell lautet der Satz, dass es ein entsprechendes Erhaltungsgesetz gibt, wenn Ihr System eine Symmetrie hat. Zum Beispiel impliziert die Vorstellung, dass die fundamentalen Gesetze der Physik heute wie morgen gleich sind (Zeitsymmetrie), dass Energie konserviert wird. Die Vorstellung, dass die Gesetze der Physik hier dieselben sind wie im Weltraum, impliziert, dass der Impuls erhalten bleibt. Symmetrie ist vielleicht das treibende Konzept in der Grundlagenphysik, vor allem aufgrund des Beitrags.“

Die Callan-Symanzik-Gleichung

„Die Callan-Symanzik-Gleichung ist eine wichtige erste-Prinzipien-Gleichung von 1970, wesentlich für die Beschreibung, wie naive Erwartungen in einer Quantenwelt scheitern werden „, sagte der theoretische Physiker Matt Strassler von der Rutgers University.

Die Gleichung hat zahlreiche Anwendungen, darunter die Möglichkeit, die Masse und Größe des Protons und des Neutrons abzuschätzen, aus denen die Atomkerne bestehen.Die Grundphysik sagt uns, dass die Gravitationskraft und die elektrische Kraft zwischen zwei Objekten proportional zur Umkehrung des Abstands zwischen ihnen im Quadrat ist. Auf einer einfachen Ebene gilt dasselbe für die starke Kernkraft, die Protonen und Neutronen zusammenhält, um die Atomkerne zu bilden, und die Quarks zusammenhält, um Protonen und Neutronen zu bilden. Winzige Quantenfluktuationen können jedoch die Abhängigkeit einer Kraft von der Entfernung geringfügig verändern, was dramatische Folgen für die starke Kernkraft hat.“Es verhindert, dass diese Kraft auf große Entfernungen abnimmt, und bewirkt, dass sie Quarks einfängt und sie zu den Protonen und Neutronen unserer Welt verbindet“, sagte Strassler. „Die Callan-Symanzik-Gleichung bezieht diesen dramatischen und schwer zu berechnenden Effekt, der wichtig ist, wenn er ungefähr die Größe eines Protons hat, auf subtilere, aber leichter zu berechnende Effekte, die gemessen werden können, wenn er viel kleiner ist als ein Proton.“

Die minimale Oberflächengleichung

„Die minimale Oberflächengleichung kodiert irgendwie die schönen Seifenfilme, die sich auf Drahtgrenzen bilden, wenn Sie sie eintauchen in Seifenwasser „, sagte der Mathematiker Frank Morgan vom Williams College. „Die Tatsache, dass die Gleichung“nichtlinear“ist und Potenzen und Produkte von Derivaten beinhaltet, ist der codierte mathematische Hinweis für das überraschende Verhalten von Seifenfilmen. Dies steht im Gegensatz zu bekannteren linearen partiellen Differentialgleichungen wie der Wärmegleichung, der Wellengleichung und der Schrödinger-Gleichung der Quantenphysik.“