Definite Integrals
Vielleicht möchten Sie zuerst die Einführung in die Integration lesen!
Integration
|
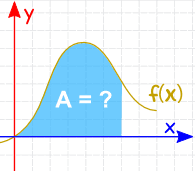
Integration kann verwendet werden, um Bereiche, Volumina, zentrale Punkte und viele nützliche Dinge zu finden. Aber es wird oft verwendet, um den Bereich unter dem Graphen einer Funktion wie folgt zu finden: |
 |
|
|
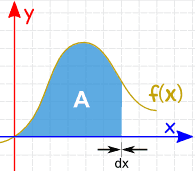
Der Bereich kann durch Hinzufügen von Slices gefunden werden, die sich der Breite von Null nähern: Und es gibt Integrationsregeln, die uns helfen, die Antwort zu erhalten. |
 |
Notation
Das Symbol für „Integral“ ist ein stilvolles „S“ (für „Summe“, die Idee, Scheiben zu summieren):
Nach dem Integralsymbol setzen wir die Funktion, deren Integral wir finden wollen (Integranden genannt).
Und beenden Sie dann mit dx , um zu bedeuten, dass die Slices in x-Richtung verlaufen (und sich in der Breite Null nähern).
Bestimmtes Integral
Ein bestimmtes Integral hat Start- und Endwerte: mit anderen Worten, es gibt ein Intervall .
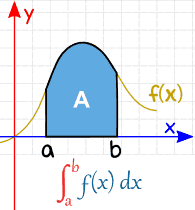
a und b (Limits, Bounds oder Boundaries genannt) werden wie folgt am unteren und oberen Rand des „S“ platziert:
 |
 |
|
| Definite Integral (from a to b) |
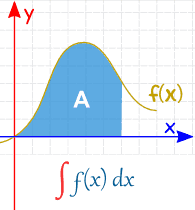
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
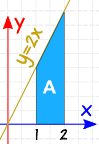
Beispiel: Was ist 2 ∫ 1 2x dx
Wir werden nach dem bestimmten Integral von 1 bis 2 von 2x dx gefragt
Zuerst müssen wir das unbestimmte Integral finden.
Nach den Integrationsregeln finden wir, dass ∫2x dx = x2 + C
Berechnen Sie nun, dass bei 1 und 2:
- Bei x=1: ∫2x dx = 12 + C
- Bei x=2: ∫2x dx = 22 + C
Subtrahieren:
Und „C“ wird aufgehoben… mit bestimmten Integralen können wir also C ignorieren.
Ergebnis:

Überprüfen Sie: Mit einer so einfachen Form versuchen wir auch, die Fläche nach Geometrie zu berechnen:
A = 2+42 × 1 = 3
Ja, es hat eine Fläche von 3.
(Juhu!)
Notation: Wir können das unbestimmte Integral (ohne das +C) in eckigen Klammern mit den Grenzen a und b wie folgt anzeigen:
Beispiel (Fortsetzung)
Eine gute Möglichkeit, Ihre Antwort zu zeigen:
=
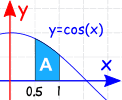
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
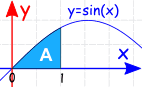
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
Das unbestimmte Integral ist: ∫sin(x) dx = −cos(x) + C
Da wir können wir von 0 aus einfach das Integral bei x = 1 berechnen?
-cos(1) = -0,540…
Was? Es ist negativ? Aber es sieht in der Grafik positiv aus.
Gut … wir haben einen Fehler gemacht!
Weil wir das Integral bei x=0 subtrahieren müssen. Wir sollten nicht davon ausgehen, dass es Null ist.
Also machen wir es richtig und subtrahieren eines vom anderen:
=
Das ist besser!
Aber wir können negative Regionen haben, wenn die Kurve unterhalb der Achse liegt:
Beispiel:
Das bestimmte Integral von 1 bis 3 von cos(x) dx:
Beachten Sie, dass ein Teil davon positiv ist , und einige negative.
Das bestimmte Integral berechnet den Nettowert.
Lassen Sie uns die Berechnungen durchführen:
=
1
Sprung gibt es mehr negativ als positiv mit dem Nettoergebnis von -0.700….
Wir müssen uns also an diese wichtige Sache erinnern:
Versuchen Sie, cos(x) mit unterschiedlichen Start- und Endwerten zu integrieren, um selbst zu sehen, wie positiv und negativ funktionieren.
Positiver Bereich
Aber manchmal möchten wir, dass alle Bereiche als positiv behandelt werden (ohne dass der Teil unterhalb der Achse subtrahiert wird).
In diesem Fall müssen wir die Flächen separat berechnen, wie in diesem Beispiel:

Beispiel: Was ist die Gesamtfläche zwischen y = cos (x) und der x-Achse von x = 1 bis x = 3?
Dies ist wie das Beispiel, das wir gerade gemacht haben, aber jetzt erwarten wir, dass alle Bereiche positiv sind (stellen Sie sich vor, wir müssten es malen).
Jetzt müssen wir also die Teile separat machen:
- Einer für den Bereich oberhalb der x-Achse
- Einer für den Bereich unterhalb der x-Achse
Die Kurve kreuzt die x-Achse bei x = π/2, so haben wir:
Von 1 bis π/2:
= sin(π/2) − sin(1)
Von π/2 bis 3:
= sin(3) − sin(π/2)
Das letzte kommt negativ heraus, aber wir wollen, dass es positiv ist, also:
Gesamtfläche = 0,159… + 0.859… = 1.018…
Dies unterscheidet sich stark von der Antwort im vorherigen Beispiel.
Continuous
Oh ja, die Funktion, die wir integrieren, muss zwischen a und b kontinuierlich sein: keine Löcher, Sprünge oder vertikalen Asymptoten (wobei die Funktion nach oben / unten in Richtung unendlich geht).
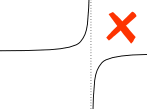
Beispiel:
Eine vertikale Asymptote zwischen a und b beeinflusst das bestimmte Integral.
Eigenschaften
Fläche oben – Fläche unten
Das Integral addiert die Fläche oberhalb der Achse, subtrahiert jedoch die Fläche darunter für einen „Nettowert“:
Funktionen hinzufügen
Das Integral von f+g ist gleich dem Integral von f plus dem Integral von g:
Intervall umkehren
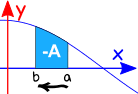
verwenden, ergibt das Umkehren der Richtung des Intervalls das Negativ der ursprünglichen Richtung.
![]()


Leave a Reply