Articles

Cohens Kappa

by admin

Cohens Kappa auswerten

Der Wert für Kappa kann kleiner als 0 (negativ) sein. Eine Punktzahl von 0 bedeutet, dass es eine zufällige Übereinstimmung zwischen den Bewertern gibt, während eine Punktzahl von 1 bedeutet, dass es eine vollständige Übereinstimmung zwischen den Bewertern gibt. Daher bedeutet eine Punktzahl, die kleiner als 0 ist, dass es weniger Übereinstimmung als Zufall gibt. Im Folgenden zeige ich Ihnen die Formel, um dies herauszufinden, aber es ist wichtig, dass Sie sich mit Abbildung 4 vertraut machen, um ein starkes Verständnis zu haben.

Der Grund, warum ich zwei Gitter hervorgehoben habe, wird gleich klar, aber lassen Sie mich vorerst jedes Gitter aufschlüsseln.

A => Die Gesamtzahl der Instanzen, von denen beide Bewerter sagten, dass sie korrekt waren. Die Rater sind sich einig.

B => Die Gesamtzahl der Instanzen, von denen Rater 2 sagte, dass sie falsch waren, aber Rater 1 sagte, dass sie korrekt waren. Dies ist eine Meinungsverschiedenheit.

C => Die Gesamtzahl der Instanzen, von denen Rater 1 sagte, dass sie falsch waren, aber Rater 2 sagte, dass sie korrekt waren. Dies ist auch eine Meinungsverschiedenheit.

D => Die Gesamtzahl der Instanzen, die von beiden Bewertern als falsch angegeben wurden. Die Rater sind sich einig.

Um den Kappa-Wert herauszufinden, müssen wir zuerst die Wahrscheinlichkeit der Übereinstimmung kennen (dies erklärt, warum ich die Übereinstimmungsdiagonale hervorgehoben habe). Diese Formel wird abgeleitet, indem die Anzahl der Tests, in denen die Rater zustimmen, addiert und dann durch die Gesamtzahl der Tests dividiert wird. Am Beispiel aus Abbildung 4 würde das bedeuten (A + D) / (A + B+ C+ D).

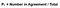
Abbildung 5: Wahrscheinlichkeit der Übereinstimmung

Perfekt! Der nächste Schritt besteht darin, die Wahrscheinlichkeit einer zufälligen Übereinstimmung zu ermitteln. Unter Verwendung von Abbildung 4 als Leitfaden ist der erwartete Wert die Gesamtzahl der Male, die Rater 1 als richtig angibt, dividiert durch die Gesamtzahl der Instanzen, multipliziert mit der Gesamtzahl der Male, die Rater 2 als richtig angibt, dividiert durch die Gesamtzahl der Instanzen, addiert zu der Gesamtzahl der Male, die Rater 1 als falsch angibt, multipliziert mit der Gesamtzahl der Male, die Rater 2 als falsch angibt. Das ist eine Menge Informationen zu nehmen in dort so in Abbildung 6 Ich habe diese Gleichung mit dem Gitter oben formuliert.

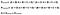
Figure 6: Formula to derive probability of random agreement

Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

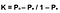
Figure 7: Cohens Kappa-Koeffizientenformel.

Großartig! Sie sind nun in der Lage, zwischen Zuverlässigkeit und Validität zu unterscheiden, Cohens Kappa zu erklären und zu bewerten. Diese Statistik ist sehr nützlich, obwohl ich, da ich verstanden habe, wie sie funktioniert, jetzt glaube, dass sie bei der Optimierung von Algorithmen für eine bestimmte Metrik möglicherweise nicht ausreichend genutzt wird. Darüber hinaus kann Cohens Kappa sowohl Probleme mit mehreren Klassen als auch Probleme mit unausgewogenen Klassen gut messen.

P.S. Wenn es etwas gibt, das ich mit Data Science zu tun haben soll, können Sie mir eine direkte Nachricht auf Twitter @KurtisPykes senden oder eine Antwort auf diesen Beitrag hinterlassen.