beanz Magazine
Karte von Merian-Erben (1652) auf Wikipedia
Das mathematische Rätsel dieses Monats stammt aus dem Jahr 1735, als es erstmals von Leonhard Euler, einem Schweizer Mathematiker und Physiker, gelöst wurde.
Das Puzzle heißt Die sieben Brücken von Königsberg. Es basiert auf einer tatsächlichen Stadt, damals in Preußen, jetzt Kaliningrad in Russland. Die Stadt wird durch einen Fluss mit zwei Inseln dazwischen geteilt und weiter flussabwärts teilt der Fluss die Stadt wieder.
Das Problem ist täuschend einfach: es gibt (oder waren zu Eulers Zeiten) sieben Brücken, die die beiden Inseln und die flussabwärts gelegenen Teile der Stadt verbinden. Euler fragte sich, ob eine Person jede der sieben Brücken einmal und nur einmal überqueren könnte, um jeden Teil der Stadt zu berühren. Das Starten und Beenden an derselben Stelle war keine Voraussetzung.
Hier ist eine Karte, mit der Sie versuchen können, das Problem selbst zu lösen:
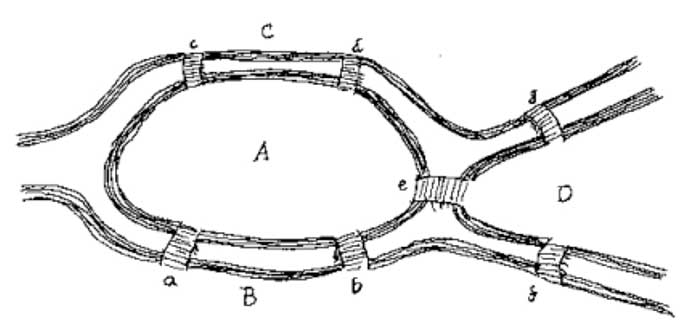
Was ist Ihrer Meinung nach wichtiger, um dieses Problem zu lösen: die Anzahl der Brücken oder die Lage jeder Brücke?
Antwort: die Anzahl der Brücken.
Euler hat bewiesen, dass die Anzahl der Brücken eine gerade Zahl sein muss, zum Beispiel sechs Brücken anstelle von sieben, wenn Sie einmal über jede Brücke gehen und zu jedem Teil von Königsberg reisen möchten. Die Lösung betrachtet jede Brücke als Endpunkt, einen Scheitelpunkt in mathematischer Hinsicht und die Verbindungen zwischen jeder Brücke (Scheitelpunkt). Euler erkannte, dass nur eine gerade Anzahl von Brücken das richtige Ergebnis lieferte, jeden Teil der Stadt berühren zu können, ohne eine Brücke zweimal zu überqueren.Euler benutzte Mathematik, um zu beweisen, dass es unmöglich war, alle sieben Brücken nur einmal zu überqueren und jeden Teil von Königsberg zu besuchen. Auf diese Weise setzte er eine Reihe von Entdeckungen und Einsichten in Gang, wie Raum und sich kreuzende Räume sowie ihre Eigenschaften definiert werden können. Eine detaillierte Beschreibung der Euler-Lösung finden Sie im Wikipedia-Link unter diesem Artikel.
Wenn Sie zum Beispiel jemals einen Mobius-Streifen gesehen haben, haben Sie ein Beispiel für Topologie gesehen, ein mathematisches Forschungsgebiet, das sich aus Eulers Lösung dieses Problems entwickelt hat. Topologie befasst sich mit Raum und wie die Dinge miteinander verbinden, sowie Kontinuität und Grenzen des Raumes. Die Topologie untersucht auch, wie sich die Eigenschaften eines Raums ändern und nicht ändern, wenn der Raum erweitert oder verkleinert wird.In der Informatik ist die Topologie nützlich, um zu verstehen, welche Netzwerke (Pfade) Daten innerhalb eines Systems fließen können und wie Datensätze miteinander in Beziehung stehen können. Die sieben Brücken von Königsberg ähneln auch einem anderen häufigen Computerproblem, das manchmal als Traveling Salesman-Problem bezeichnet wird, bei dem Sie versuchen, die effizienteste Route zu finden, wenn Sie eine Reihe von Einschränkungen wie die sieben Brücken in Eulers Problem haben.Nicht-Mathematiker (wahrscheinlich Sie, definitiv ich) erleben das Problem des reisenden Verkäufers jedes Mal, wenn wir in einen Zug oder Bus steigen. Das Problem des reisenden Verkäufers besteht darin, den effizientesten Weg zu finden, um zwischen Paaren von Städten mit bestimmten Entfernungen zu reisen. Die Verwaltung knapper Ressourcen (Züge, Busse), die auf endlichen Strecken fahren, ist ein perfektes Problem für die Datenverarbeitung, da Computer schneller und effizienter sind. Aber zuerst brauchen wir Euler und andere, um das Problem zu erklären und Lösungen mit Mathematik zu definieren. Wir programmieren dann unsere Computer, um die Mathematik zu machen.Die Topologie befasst sich auch mit der Mengenlehre, wie Gruppen von Dingen in Mengen sortiert werden können, um gemeinsame Elemente mit anderen Gruppen sowie eindeutige Elemente zu identifizieren. Ein Venn-Diagramm ist ein großartiges Beispiel für ein Set. Und die Programmierung muss manchmal Daten auf verschiedene Arten sortieren. Welche Sortiermethode für eine Situation am besten geeignet ist, kann durch die Mengenlehre bestimmt werden.
Und was geschah mit den sieben Brücken aus Eulers Zeit? Zwei Brücken wurden abgerissen und durch eine einzige Autobahn ersetzt. Von den drei verbliebenen Brücken wurde 1935 eine wieder aufgebaut, während die beiden anderen intakt blieben, wie Euler sie kannte. Und natürlich hat Königsberg, Preußen, seinen Namen in Kaliningrad, Russland, geändert.
Leave a Reply