Energetik der Ionenbindungsbildung

Ionenbindungen entstehen, wenn positiv und negativ geladene Ionen durch elektrostatische Kräfte zusammengehalten werden. Betrachten Sie ein einzelnes Ionenpaar, ein Kation und ein Anion. Wie stark wird die Kraft ihrer Anziehung sein? Nach dem Coulombschen Gesetz ist die Energie der elektrostatischen Anziehung (\(E\)) zwischen zwei geladenen Teilchen proportional zur Größe der Ladungen und umgekehrt proportional zum inneren Kernabstand zwischen den Teilchen (\(r \)):

\

\

wobei die Ladung jedes Ions durch das Symbol Q dargestellt wird. Die Proportionalitätskonstante k ist gleich 2,31 × 10-28 J·m. Dieser Wert von k enthält die Ladung eines einzelnen Elektrons (1,6022 × 10-19 C) für jedes Ion. Die Gleichung kann auch unter Verwendung der Ladung jedes Ions geschrieben werden, ausgedrückt in Coulombs (C), die in der Konstante enthalten sind. In diesem Fall ist die Proportionalitätskonstante k gleich 8,999 × 109 J · m / C2. Im angegebenen Beispiel ist Q1 = +1 (1,6022 × 10-19 C) und Q2 = -1 (1,6022 × 10-19 C). Wenn Q1 und Q2 entgegengesetzte Vorzeichen haben (wie zum Beispiel in NaCl, wo Q1 +1 für Na + und Q2 -1 für Cl− ist), dann ist E negativ, was bedeutet, dass Energie freigesetzt wird, wenn entgegengesetzt geladene Ionen aus unendlicher Entfernung zusammengebracht werden, um ein isoliertes Ionenpaar zu bilden.

Energie wird immer freigesetzt, wenn eine Bindung gebildet wird, und dementsprechend benötigt es immer Energie, um eine Bindung zu brechen.

Wie die grüne Kurve in der unteren Hälfte der Abbildung \(\pageIndex{1}\) zeigt, würde die maximale Energie freigesetzt, wenn die Ionen bei r = 0 unendlich nahe beieinander liegen. Da Ionen Raum einnehmen und eine Struktur haben, bei der der positive Kern von Elektronen umgeben ist, können sie jedoch nicht unendlich nahe beieinander liegen. Bei sehr kurzen Entfernungen werden abstoßende Elektron-Elektron-Wechselwirkungen zwischen Elektronen auf benachbarten Ionen stärker als die attraktiven Wechselwirkungen zwischen Ionen mit entgegengesetzten Ladungen, wie die rote Kurve in der oberen Hälfte von Abbildung \(\ pageIndex {1}\) zeigt. Die Gesamtenergie des Systems ist ein Gleichgewicht zwischen den attraktiven und abstoßenden Wechselwirkungen. Die violette Kurve in Abbildung \(\pageIndex{1}\) zeigt, dass die Gesamtenergie des Systems ein Minimum bei r0 erreicht, dem Punkt, an dem die elektrostatischen Abstoßungen und Anziehungen genau ausgeglichen sind. Dieser Abstand ist der gleiche wie der experimentell gemessene Bindungsabstand.

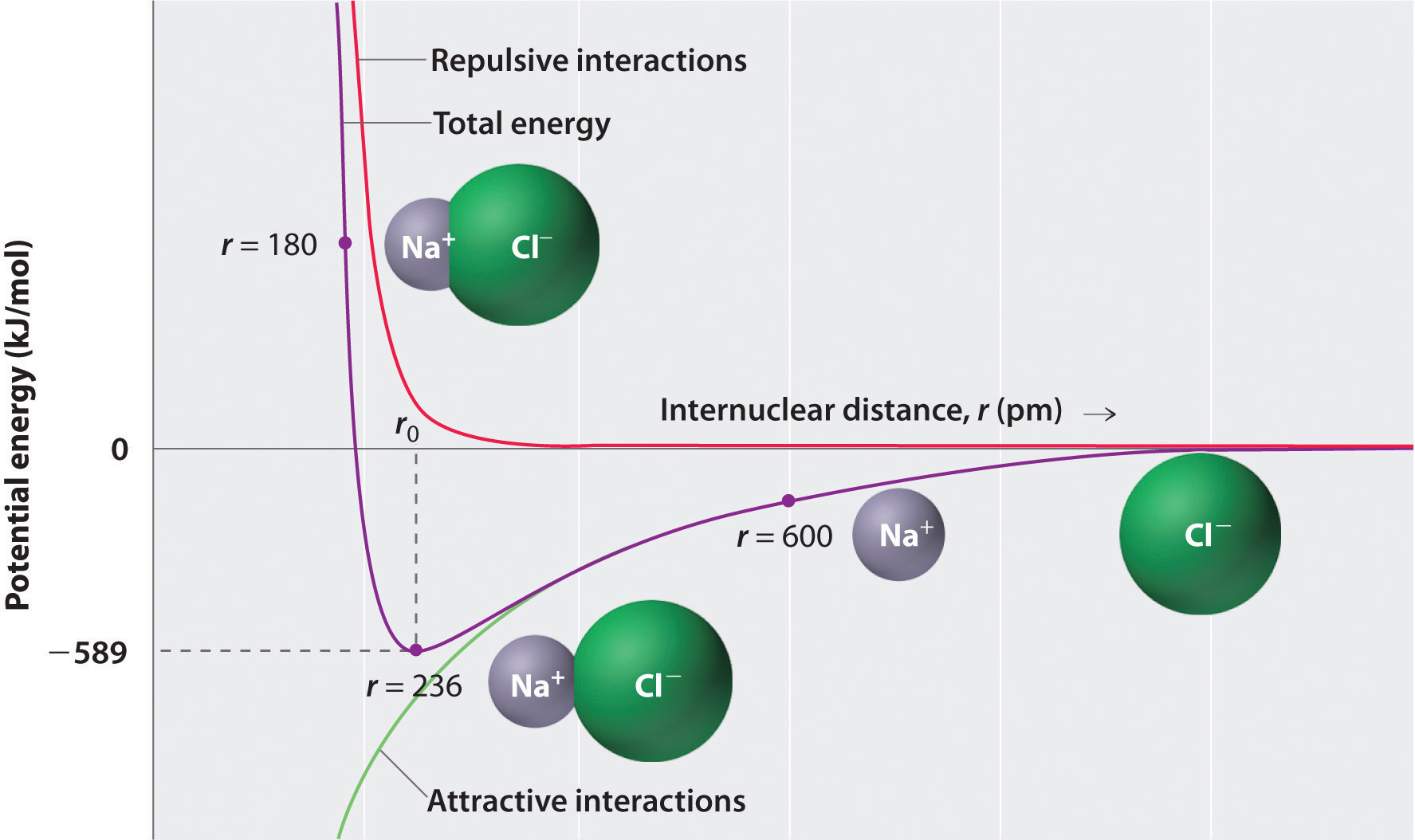
Betrachten Sie die Energie, die freigesetzt wird, wenn ein gasförmiges \(Na^ +\) -Ion und ein gasförmiges \(Cl^ -\) -Ion von r = ∞ zu r = r0 zusammengeführt werden. Da der beobachtete Gasphasen-Internuklearabstand 236 pm beträgt, ist die Energieänderung, die mit der Bildung eines Ionenpaares aus einem \(Na ^+_{(g)}\) -Ion und einem \(Cl^ -_{(g)}\) -Ion verbunden ist, wie folgt:

\ &= (2,31 \times {10^{ – 28}}\rm{J}\cdot \rm{m} ) \left( \dfrac{( + 1)( – 1)}{236\; \ abbrechen {pm} \mal 10 ^{ – 12} \abbrechen{m/pm}} \rechts) \\ &= – 9.79 \times 10^{ – 19}\; J/ion\; pair \label{Eq2} \end{align*}\]

Der negative Wert zeigt an, dass Energie freigesetzt wird. Unsere Konvention ist, dass, wenn ein chemischer Prozess Energie an die Außenwelt liefert, die Energiewende negativ ist. Wenn es Energie benötigt, ist die Energiewende positiv. Um die Energieänderung bei der Bildung eines Mols von NaCl-Paaren zu berechnen, müssen wir die Energie pro Ionenpaar mit der Avogadro-Zahl multiplizieren:

\

Dies ist die Energie, die freigesetzt wird, wenn 1 mol gasförmige Ionenpaare gebildet werden, nicht wenn 1 mol positive und negative Ionen zu einem Kristallgitter kondensieren. Diese Energie entspricht aufgrund weiträumiger Wechselwirkungen in der Gitterstruktur nicht direkt der Gitterenergie des kristallinen Festkörpers. Der große negative Wert zeigt jedoch an, dass das Zusammenbringen von positiven und negativen Ionen energetisch sehr günstig ist, unabhängig davon, ob ein Ionenpaar oder ein Kristallgitter gebildet wird.

Wir fassen die wichtigen Punkte zur Ionenbindung zusammen:

• Bei r0 sind die Ionen stabiler (haben eine geringere potentielle Energie) als in einem unendlichen inneren Kernabstand. Wenn entgegengesetzt geladene Ionen von r = ∞ zu r = r0 zusammengebracht werden, wird die Energie des Systems gesenkt (Energie wird freigesetzt).
• Wegen der niedrigen potentiellen Energie bei r0 muss dem System Energie hinzugefügt werden, um die Ionen zu trennen. Die benötigte Energiemenge ist die Bindungsenergie.
• Die Energie des Systems erreicht ein Minimum in einem bestimmten inneren Kernabstand (der Bindungsabstand).