Äquivalente Brüche verstehen

Äquivalente Brüche repräsentieren denselben Teil eines Ganzen

Der beste Weg, über äquivalente Brüche nachzudenken, ist, dass sie Brüche sind, die den gleichen Gesamtwert haben.

Wenn wir beispielsweise einen Kuchen genau in der Mitte in zwei gleich große Stücke schneiden, entspricht ein Stück der Hälfte des Kuchens.

Und wenn ein anderer Kuchen (die gleiche Größe) in 4 gleiche Stücke geschnitten wird, dann repräsentieren zwei Stücke dieses Kuchens die gleiche Menge an Kuchen, die 1/2 gemacht hat.

Wir können also sagen, dass 1/2 äquivalent (oder gleich) zu 2/4 ist.

Lassen Sie sich nicht von äquivalenten Brüchen verwirren!

Schauen Sie sich die vier Kreise oben an.Können Sie sehen, dass die eine „1/2“, die beiden „1/4“ und die vier „1/8“ für ihren Kreis die gleiche orangefarbene Fläche einnehmen?Nun, das bedeutet, dass jeder orange gefärbte Bereich ein äquivalenter Bruchteil oder eine gleiche Menge ist. Daher können wir sagen, dass 1/2 gleich 2/4 und 1/2 auch gleich 4/8 ist. Und ja Heuschrecke, 2/4 ist ein äquivalenter Bruch für 4/8 too.As sie wissen bereits, wir sind verrückt nach Regeln. Schauen wir uns also die Regel an, um zu überprüfen, ob zwei Brüche gleichwertig oder gleich sind. Die Regel für äquivalente Brüche kann etwas schwer zu erklären sein, aber halten Sie durch, wir werden die Dinge in kürze klären.

Hier ist die Regel

Diese Regel besagt, dass zwei Brüche nur dann äquivalent (gleich) sind, wenn das Produkt aus dem Zähler (a) des ersten Bruchs und dem Nenner (d) des anderen Bruchs gleich dem Produkt aus der Nenner (b) des ersten Bruchs und der Zähler (c) des anderen Bruchs.

Ein Produkt bedeutet einfach, dass Sie multiplizieren.

Das klingt nach einem Schluck, also versuchen wir es mit Zahlen…

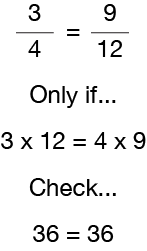
Testen Sie die Regel

Jetzt stecken wir die Zahlen in die Regel für äquivalente Brüche, um sicherzugehen, dass Sie es „kalt“ haben. 3/4 ist nur dann äquivalent (gleich) zu 9/12, wenn das Produkt aus dem Zähler (3) des ersten Bruchs und dem Nenner (12) des anderen Bruchs gleich dem Produkt aus dem Nenner (4) des ersten Bruchs und dem Zähler (9) des anderen Bruchs ist. Wir wissen also, dass 3/4 9/12 entspricht, weil 3 × 12 = 36 und 4 × 9 = 36. Eine einfache Möglichkeit, nach äquivalenten Brüchen zu suchen, besteht darin, das sogenannte „Kreuzmultiplizieren“ durchzuführen, dh den Zähler eines Bruchs mit dem Nenner des anderen Bruchs zu multiplizieren. Dann mach das Gleiche umgekehrt. Vergleichen Sie nun die beiden Antworten, um festzustellen, ob sie gleich sind. Wenn sie gleich sind, sind die beiden Brüche äquivalente Brüche.

Die folgende Grafik zeigt Ihnen, wie Sie kreuzmultiplizieren …

Okay, machen wir eine mit Zahlen, bei denen die Brüche nicht äquivalent sind …

Wie Sie an diesem Beispiel sehen können, ist 1/2 kein äquivalenter Bruch von 2/3.

Wenn Sie daran denken, die Kreuzmultiplikationsmethode zu verwenden, sollten Sie keine Probleme haben, äquivalente Brüche zu überprüfen.

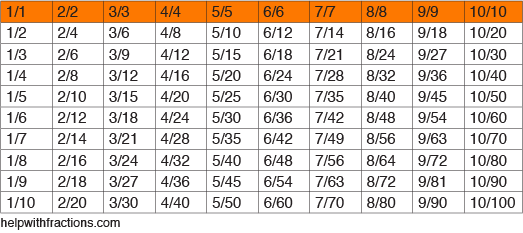
Die folgende Tabelle listet einige gängige Brüche und ihre Äquivalente auf. Lesen Sie einfach die Tabelle von links nach rechts. Was es Ihnen zeigt, sind Werte multipliziert mit verschiedenen Variationen von Brüchen gleich „1“. Sie erinnern sich, dass jede Zahl geteilt durch sich selbst gleich „1“ ist, oder?