ange Siffror separerade med kommatecken för att beräkna.

relaterad Statistikkalkylator | Standardavvikelsekalkylator/Provstorlekskalkylator

medelvärde

ordet medelvärde, som är en homonym för flera andra ord på engelska, är lika tvetydigt även inom matematikområdet. Beroende på sammanhanget, vare sig matematiskt eller statistiskt, vad menas med ”medelvärdet” förändringar. I sin enklaste matematiska definition avseende datamängder är det använda medelvärdet det aritmetiska medelvärdet, även kallat matematisk förväntan, eller medelvärde. I denna form hänvisar medelvärdet till ett mellanvärde mellan en diskret uppsättning siffror, nämligen summan av alla värden i datamängden dividerad med det totala antalet värden. Ekvationen för beräkning av ett aritmetiskt medelvärde är praktiskt taget identiskt med det för beräkning av de statistiska begreppen population och provmedelvärde, med små variationer i de använda variablerna:

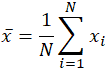
medelvärdet betecknas ofta som x, uttalas ”x bar” och även i andra användningsområden när variabeln inte är x, är barnotationen en vanlig indikator på någon form av medelvärde. I det specifika fallet med populationen betyder, snarare än att använda variabeln x, används den grekiska symbolen mu, eller Audrey. På samma sätt, eller snarare förvirrande, anges provmedlet i statistik ofta med ett kapital X. Med tanke på datamängden 10, 2, 38, 23, 38, 23, 21, tillämpa summan över avkastningen:

som tidigare nämnts är detta en av de enklaste definitionerna av medelvärdet, och vissa andra inkluderar det vägda aritmetiska medelvärdet (som bara skiljer sig åt genom att vissa värden i datauppsättningen bidrar med mer värde än andra) och geometriskt medelvärde. Korrekt förståelse av givna situationer och sammanhang kan ofta ge en person de verktyg som behövs för att bestämma vilken statistiskt relevant metod som ska användas. I allmänhet bör medelvärde, median, läge och intervall helst beräknas och analyseras för ett givet prov eller datamängd eftersom de belyser olika aspekter av den givna data, och om de betraktas ensamma, kan leda till felaktiga representationer av data, vilket kommer att visas i följande avsnitt.

Median

det statistiska begreppet median är ett värde som delar upp ett dataprov, population eller sannolikhetsfördelning i två halvor. Att hitta medianen innebär i huvudsak att hitta värdet i ett dataprov som har en fysisk plats mellan resten av siffrorna. Observera att vid beräkning av medianen för en ändlig lista med siffror är ordningen på dataproverna viktig. Konventionellt listas värdena i stigande ordning, men det finns ingen verklig anledning att lista värdena i fallande ordning skulle ge olika resultat. Om det totala antalet värden i ett dataprov är udda är medianen helt enkelt numret mitt i listan över alla värden. När dataprovet innehåller ett jämnt antal värden är medianen medelvärdet för de två mellanvärdena. Även om detta kan vara förvirrande, kom bara ihåg att även om medianen ibland innebär beräkning av ett medelvärde, när det här fallet uppstår, kommer det bara att involvera de två mellanvärdena, medan ett medelvärde involverar alla värden i dataprovet. I de udda fall där det bara finns två dataprover eller det finns ett jämnt antal prover där alla värden är desamma, kommer medelvärdet och medianen att vara desamma. Med tanke på samma datamängd som tidigare skulle medianen förvärvas på följande sätt:

2,10,21,23,23,38,38

Efter att ha listat data i stigande ordning och bestämt att det finns ett udda antal värden är det uppenbart att 23 är medianen givet detta fall. Om det fanns ett annat värde till datamängden:

2,10,21,23,23,38,38,1027892

eftersom det finns ett jämnt antal värden kommer medianen att vara medelvärdet av de två mittentalen, i detta fall 23 och 23, vars medelvärde är 23. Observera att i denna speciella datamängd har tillägget av en outlier (ett värde långt utanför det förväntade värdet), värdet 1,027,892, ingen verklig effekt på datamängden. Om medelvärdet beräknas för denna datamängd är resultatet 128 505,875. Detta värde är uppenbarligen inte en bra representation av de sju andra värdena i datamängden som är mycket mindre och närmare i värde än genomsnittet och outlier. Detta är den största fördelen med att använda medianen för att beskriva statistiska data jämfört med medelvärdet. Medan både, liksom andra statistiska värden, bör beräknas när man beskriver data, om endast en kan användas, kan medianen ge en bättre uppskattning av ett typiskt värde i en given datamängd när det finns extremt stora variationer mellan värden.

läge

i statistik är läget värdet i en datamängd som har det högsta antalet återfall. Det är möjligt för en datauppsättning att vara multimodal, vilket innebär att den har mer än ett läge. Till exempel:

2,10,21,23,23,38,38

både 23 och 38 visas två gånger vardera, vilket gör dem båda ett läge för datauppsättningen ovan. på samma sätt som medelvärde och median används läget som ett sätt att uttrycka information om slumpmässiga variabler och populationer. Till skillnad från medelvärde och median är läget dock ett koncept som kan tillämpas på icke-numeriska värden som varumärket tortillachips som oftast köps från en livsmedelsbutik. När man till exempel jämför varumärkena Tostitos, Mission och XOCHiTL, om det konstateras att vid försäljning av tortillachips är XOCHiTL läget och säljer i ett 3:2:1-förhållande jämfört med Tostitos respektive Mission brand tortilla chips, kan förhållandet användas för att bestämma hur många påsar av varje märke som ska lagras. I det fall där 24 påsar med tortillachips säljer under en viss period skulle butiken lagra 12 påsar med XOCHiTL-chips, 8 av Tostitos och 4 av uppdrag om du använder läget. Om butiken bara använde ett genomsnitt och sålde 8 påsar av varje, kan det potentiellt förlora 4-försäljningen om en kund bara önskade XOCHiTL-chips och inte något annat märke. Som framgår av detta exempel är det viktigt att ta hänsyn till alla sätt av statistiska värden när man försöker dra slutsatser om något dataprov.

intervall

intervallet för en datamängd i statistiken är skillnaden mellan de största och de minsta värdena. Medan intervallet har olika betydelser inom olika områden av statistik och matematik, är detta dess mest grundläggande definition, och är vad som används av den medföljande räknaren. Med samma exempel:

2,10,21,23,23,38,38
38 – 2 = 36

intervallet i detta exempel är 36. På samma sätt som medelvärdet kan intervallet påverkas avsevärt av extremt stora eller små värden. Använda samma exempel som tidigare: