Linjär regressionsanalys i Excel
handledningen förklarar grunderna för regressionsanalys och visar några olika sätt att göra linjär regression i Excel.
Föreställ dig detta: du får en hel del olika data och ombeds att förutsäga nästa års försäljningsnummer för ditt företag. Du har upptäckt dussintals, kanske till och med hundratals, faktorer som eventuellt kan påverka siffrorna. Men hur vet du vilka som verkligen är viktiga? Kör regressionsanalys i Excel. Det kommer att ge dig ett svar på detta och många fler frågor: Vilka faktorer spelar roll och vilka kan ignoreras? Hur nära är dessa faktorer relaterade till varandra? Och hur säker kan du vara om förutsägelserna?
- regressionsanalys i Excel
- linjär regression i Excel med Analysverktygspak
- rita en linjär regressionsgraf
- regressionsanalys i Excel med formler
regressionsanalys i Excel-grunderna
i statistisk modellering används regressionsanalys för att uppskatta förhållandena mellan två eller flera variabler:
beroende variabel (aka criterion variabel) är den viktigaste faktorn du försöker förstå och förutsäga.
oberoende variabler (aka förklarande variabler eller prediktorer) är de faktorer som kan påverka den beroende variabeln.
regressionsanalys hjälper dig att förstå hur den beroende variabeln ändras när en av de oberoende variablerna varierar och gör det möjligt att matematiskt bestämma vilken av dessa variabler som verkligen påverkar.tekniskt sett är en regressionsanalysmodell baserad på summan av kvadrater, vilket är ett matematiskt sätt att hitta spridningen av datapunkter. Målet med en modell är att få den minsta möjliga summan av kvadrater och rita en linje som kommer närmast data.
i statistik skiljer de mellan en enkel och multipel linjär regression. Enkel linjär regression modellerar förhållandet mellan en beroende variabel och en oberoende variabler med hjälp av en linjär funktion. Om du använder två eller flera förklarande variabler för att förutsäga den beroende variabeln, hanterar du multipel linjär regression. Om den beroende variabeln modelleras som en icke-linjär funktion eftersom datarelationerna inte följer en rak linje, använd istället olinjär regression. Fokus för denna handledning kommer att ligga på en enkel linjär regression.
som ett exempel, låt oss ta försäljningsnummer för paraplyer under de senaste 24 månaderna och ta reda på den genomsnittliga månatliga Nederbörden för samma period. Rita denna information på ett diagram, och regressionslinjen kommer att visa förhållandet mellan den oberoende variabeln (regn) och beroende variabel (paraplyförsäljning):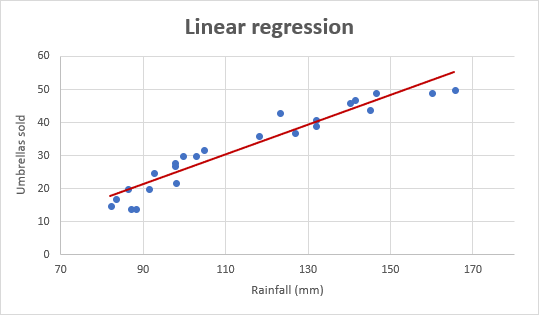
linjär regressionsekvation
matematiskt definieras en linjär regression av denna ekvation:
där:
- x är en oberoende variabel.
- y är en beroende variabel.
- a är y-intercept, vilket är det förväntade medelvärdet för y när alla X-variabler är lika med 0. På en regressionsgraf är det den punkt där linjen korsar Y-axeln.
- b är lutningen på en regressionslinje, vilket är förändringshastigheten för y som X ändras.
- är den slumpmässiga feltermen, vilket är skillnaden mellan det faktiska värdet av en beroende variabel och dess förutsagda värde.
den linjära regressionsekvationen har alltid en felterm eftersom prediktorer i verkligheten aldrig är helt exakta. Vissa program, inklusive Excel, gör dock felberäkningen bakom kulisserna. Så i Excel gör du linjär regression med minsta kvadratmetoden och söker koefficienter A och b så att:
för vårt exempel tar den linjära regressionsekvationen följande form:
Umbrellas sold = b * rainfall + a
det finns en handfull olika sätt att hitta a och b. de tre huvudmetoderna för att utföra linjär regressionsanalys i Excel är:
- Regression tool medföljer Analysis ToolPak
- scatterdiagram med en trendlinje
- linjär regressionsformel
nedan hittar du detaljerade instruktioner om hur du använder varje metod.
hur man gör linjär regression i Excel med Analysis ToolPak
detta exempel visar hur man kör regression i Excel med hjälp av ett specialverktyg som ingår i Analysis ToolPak-tillägget.
aktivera tillägget Analysis ToolPak
Analysis ToolPak är tillgängligt i alla versioner av Excel 2019 till 2003 men är inte aktiverat som standard. Så du måste slå på den manuellt. Så här:
- i Excel klickar du på Arkiv> alternativ.
- i dialogrutan Excel-alternativ väljer du Tillägg i den vänstra sidofältet, kontrollerar att Excel-tillägg är markerade i rutan hantera och klickar på Gå.
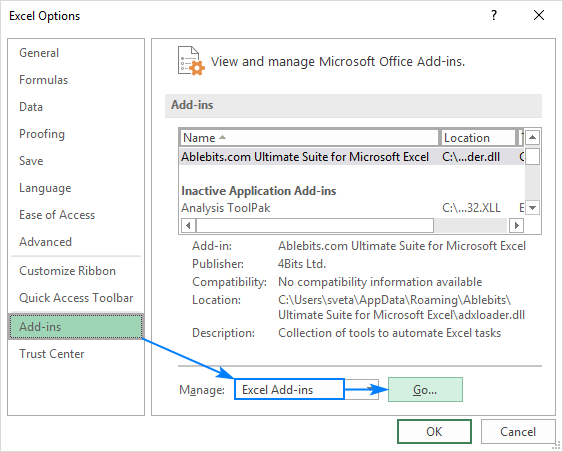
- i dialogrutan Tillägg markerar du Analysis Toolpak och klickar på OK:

detta lägger till dataanalysverktygen på fliken Data i ditt Excel-band.
kör regressionsanalys
i det här exemplet ska vi göra en enkel linjär regression i Excel. Vad vi har är en lista över genomsnittlig månatlig nederbörd under de senaste 24 månaderna i kolumn B, som är vår oberoende variabel (prediktor), och antalet paraplyer som säljs i kolumn C, vilket är den beroende variabeln. Naturligtvis finns det många andra faktorer som kan påverka försäljningen, men för närvarande fokuserar vi bara på dessa två variabler: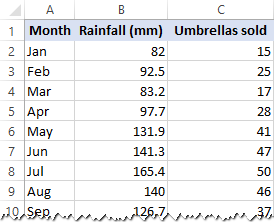
med Analysis Toolpak tillagd aktiverad, utför dessa steg för att utföra regressionsanalys i Excel:
- på fliken Data, i analysgruppen, klicka på knappen dataanalys.

- Välj Regression och klicka på OK.

- i regressionsdialogrutan konfigurerar du följande inställningar:
- Välj inmatningsområdet Y, vilket är din beroende variabel. I vårt fall är det paraplyförsäljning (C1:C25).
- Välj Input X-intervallet, dvs. din oberoende variabel. I det här exemplet är det den genomsnittliga månatliga nederbörden (B1:B25).
om du bygger en multipel regressionsmodell väljer du två eller flera intilliggande kolumner med olika oberoende variabler.
- markera rutan etiketter om det finns rubriker högst upp i dina x-och Y-intervall.
- Välj önskat Utmatningsalternativ, ett nytt kalkylblad i vårt fall.
- markera kryssrutan Residuals för att få skillnaden mellan de förutsagda och faktiska värdena.
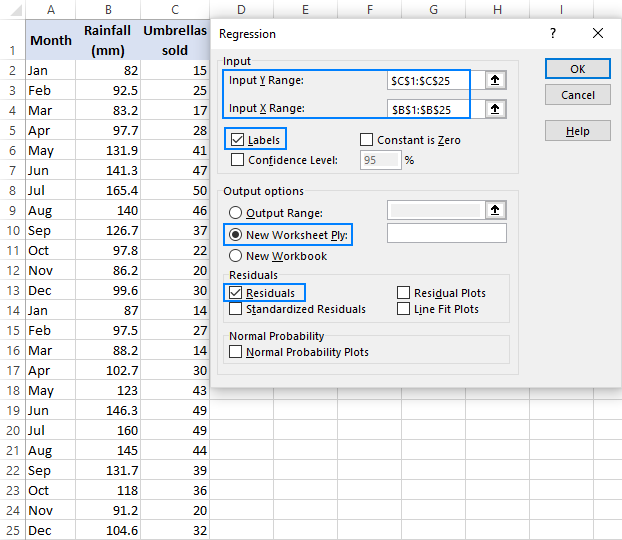
- Klicka på OK och observera regressionsanalysutgången som skapats av Excel.
tolka regressionsanalysutgång
som du just har sett är det enkelt att köra regression i Excel eftersom alla beräkningar förformas automatiskt. Tolkningen av resultaten är lite svårare eftersom du behöver veta vad som ligger bakom varje nummer. Nedan hittar du en uppdelning av 4 stora delar av regressionsanalysutgången.
Regressionsanalysutgång: Sammanfattningsutgång
denna del berättar hur väl den beräknade linjära regressionsekvationen passar dina källdata.

här är vad varje information betyder:
multipel R. Det är korrelationskoefficienten som mäter styrkan i ett linjärt förhållande mellan två variabler. Korrelationskoefficienten kan vara vilket värde som helst mellan -1 och 1, och dess absoluta värde indikerar förhållandestyrkan. Ju större absolut värde desto starkare förhållandet:
- 1 betyder ett starkt positivt förhållande
- -1 betyder ett starkt negativt förhållande
- 0 betyder inget förhållande alls
R kvadrat. Det är bestämningskoefficienten, som används som en indikator på passformen. Det visar hur många poäng som faller på regressionslinjen. R2-värdet beräknas utifrån den totala summan av kvadrater, mer exakt är det summan av de kvadrerade avvikelserna för de ursprungliga uppgifterna från medelvärdet.
i vårt exempel är R2 0,91 (avrundat till 2 siffror), vilket är fairy bra. Det betyder att 91% av våra värden passar regressionsanalysmodellen. Med andra ord förklaras 91% av de beroende variablerna (y-värden) av de oberoende variablerna (x-värden). Generellt anses R kvadrat på 95% eller mer vara en bra passform.
justerad R-kvadrat. Det är R-torget justerat för antalet oberoende variabler i modellen. Du vill använda detta värde istället för R-kvadrat för multipel regressionsanalys.
standardfel. Det är en annan godhet-of-fit åtgärd som visar precisionen i din regressionsanalys – ju mindre antal, desto säkrare kan du vara om din regressionsekvation. Medan R2 representerar procentandelen av de beroende variablerna varians som förklaras av modellen, är standardfel ett absolut mått som visar det genomsnittliga avståndet som datapunkterna faller från regressionslinjen.
observationer. Det är helt enkelt antalet observationer i din modell.
Regressionsanalysutgång: ANOVA
den andra delen av produktionen är variansanalys (ANOVA):

i grund och botten delar den summan av kvadrater i enskilda komponenter som ger information om variabilitetsnivåerna inom din regressionsmodell:
- df är antalet frihetsgrader associerade med varianskällorna.
- SS är summan av kvadrater. Ju mindre resterande SS jämfört med den totala SS, desto bättre passar din modell data.
- MS är medelkvadrat.
- F är f-statistiken eller f-testet för nollhypotesen. Det används för att testa modellens övergripande betydelse.
- betydelse F är p-värdet på F.
ANOVA-delen används sällan för en enkel linjär regressionsanalys i Excel, men du bör definitivt titta närmare på den sista komponenten. Betydelsen F-värdet ger en uppfattning om hur tillförlitliga (statistiskt signifikanta) dina resultat är. Om betydelsen F är mindre än 0,05 (5%) är din modell OK. Om det är större än 0,05, skulle du förmodligen bättre välja en annan oberoende variabel.
Regressionsanalysutgång: koefficienter
det här avsnittet innehåller specifik information om komponenterna i din analys:
den mest användbara komponenten i detta avsnitt är koefficienter. Det gör att du kan bygga en linjär regressionsekvation i Excel:
För vår datamängd, där y är antalet sålda paraplyer och x är en genomsnittlig månatlig nederbörd, går vår linjära regressionsformel enligt följande:
Y = Rainfall Coefficient * x + Intercept
utrustad med A-och B-värden avrundade till tre decimaler, blir den till en:
Y=0.45*x-19.074
till exempel, med den genomsnittliga månatliga nederbörden lika med 82 mm, skulle paraplyförsäljningen vara ungefär 17,8:
0.45*82-19.074=17.8
på liknande sätt kan du ta reda på hur många paraplyer som ska säljas med någon annan månatlig nederbörd (X variabel) du anger.
Regressionsanalysutgång: rester
om du jämför det uppskattade och faktiska antalet sålda paraplyer som motsvarar den månatliga Nederbörden på 82 mm ser du att dessa siffror är något annorlunda:
- beräknad: 17.8 (beräknat ovan)
- faktisk: 15 (rad 2 i källdata)
varför är skillnaden? Eftersom oberoende variabler aldrig är perfekta prediktorer för de beroende variablerna. Och resterna kan hjälpa dig att förstå hur långt de faktiska värdena är från de förutspådda värdena:
hur man gör en linjär regressionsgraf i Excel
om du snabbt behöver visualisera förhållandet mellan de två variablerna, rita ett linjärt regressionsschema. Det är väldigt enkelt! Så här:
- Välj de två kolumnerna med dina data, inklusive rubriker.
- på fliken infälld, i gruppen chattar, klicka på ikonen scatterdiagram och välj Scatterminiatyren (den första):
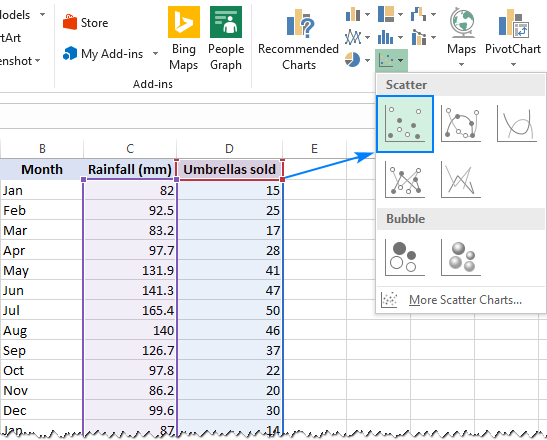
detta kommer att infoga en scatterdiagram i ditt kalkylblad, som kommer att likna den här:

- nu måste vi rita minst en scatterdiagram i ditt kalkylblad, som kommer att likna den här:

- kvadrater regression linje. För att få det gjort, högerklicka på vilken punkt som helst och välj Lägg till trendlinje… från snabbmenyn.

- i den högra rutan väljer du den linjära trendlineformen och kontrollerar eventuellt Visningsekvationen på diagrammet för att få din regressionsformel:
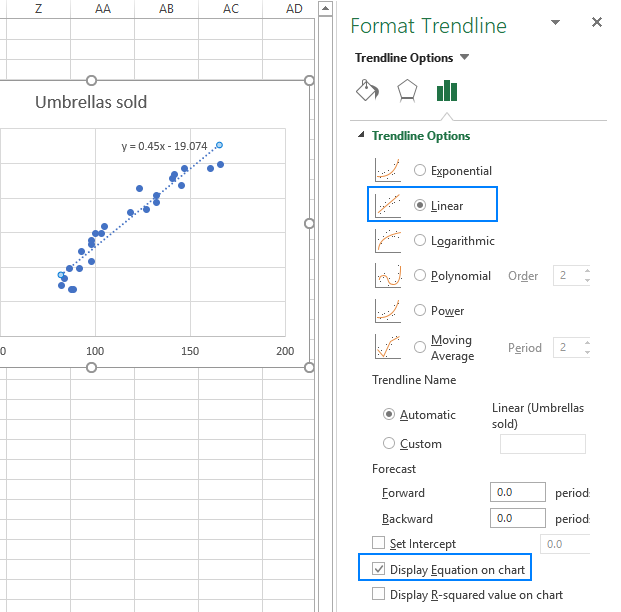
som du kanske märker är regressionsekvationen Excel skapad för oss samma som den linjära regressionsformeln vi byggde baserat på Koefficienternas utgång.
- Byt till Fill & Linjefliken och anpassa linjen efter eget tycke. Du kan till exempel välja en annan linjefärg och använda en solid linje istället för en streckad linje (välj Solid linje i rutan Strecktyp):

vid denna punkt ser ditt diagram redan ut som en anständig regressionsgraf:
ändå kanske du vill göra några fler förbättringar:
- dra ekvationen var du vill.
- Lägg axlar titlar (Diagram element knapp > axel titlar).
- Om dina datapunkter börjar mitt i den horisontella och / eller vertikala axeln som i det här exemplet kanske du vill bli av med det överdrivna vita utrymmet. Följande tips förklarar hur du gör detta: skala diagramaxlarna för att minska det vita utrymmet.
och så här ser vår förbättrade regressionsgraf ut:
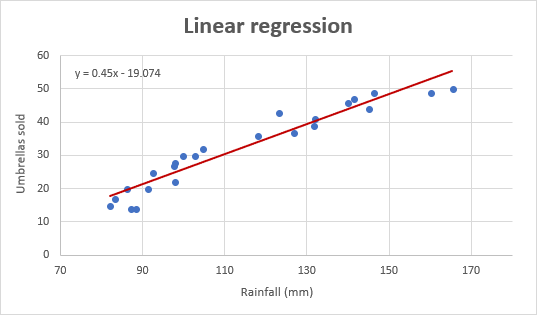 viktigt! I regressionsgrafen bör den oberoende variabeln alltid vara på X-axeln och den beroende variabeln på Y-axeln. Om diagrammet ritas i omvänd ordning byter du kolumnerna i kalkylbladet och ritar sedan diagrammet på nytt. Om du inte får ordna om källdata kan du byta X-och Y-axlarna direkt i ett diagram.
viktigt! I regressionsgrafen bör den oberoende variabeln alltid vara på X-axeln och den beroende variabeln på Y-axeln. Om diagrammet ritas i omvänd ordning byter du kolumnerna i kalkylbladet och ritar sedan diagrammet på nytt. Om du inte får ordna om källdata kan du byta X-och Y-axlarna direkt i ett diagram.
hur man gör regression i Excel med formler
Microsoft Excel har några statistiska funktioner som kan hjälpa dig att göra linjär regressionsanalys som LINEST, SLOPE, INTERCPET och CORREL.
funktionen LINEST använder regressionsmetoden för minsta kvadrater för att beräkna en rak linje som bäst förklarar förhållandet mellan dina variabler och returnerar en matris som beskriver den linjen. Du hittar den detaljerade förklaringen av funktionens syntax i den här handledningen. För nu, låt oss bara göra en formel för vårt provdataset:
=LINEST(C2:C25, B2:B25)
eftersom LINEST-funktionen returnerar en rad värden måste du ange den som en matrisformel. Välj två intilliggande celler i samma rad, E2:F2 i vårt fall skriver du formeln och trycker på Ctrl + Shift + Enter för att slutföra den.
formeln returnerar B-koefficienten (E1) och A-konstanten (F1) för den redan kända linjära regressionsekvationen:
y = bx + a

om du undviker att använda matrisformler i dina kalkylblad kan du beräkna A och b individuellt med vanliga formler:
hämta y-intercept (a):
=INTERCEPT(C2:C25, B2:B25)
hämta lutningen (B):
=SLOPE(C2:C25, B2:B25)
dessutom kan du hitta korrelationskoefficienten (multipel R i sammanfattningsutgången för regressionsanalys) som indikerar hur starkt de två variablerna är relaterade till varandra:
=CORREL(B2:B25,C2:C25)
följande skärmdump visar alla dessa Excel-regressionsformler i aktion:
det är så du gör linjär regression i Excel. Som sagt, Kom ihåg att Microsoft Excel inte är ett statistiskt program. Om du behöver utföra regressionsanalys på professionell nivå kanske du vill använda riktad programvara som XLSTAT, RegressIt, etc.
tillgängliga nedladdningar:
för att titta närmare på våra linjära regressionsformler och andra tekniker som diskuteras i denna handledning är du välkommen att ladda ner vår Provregressionsanalys i Excel-arbetsbok.
- hur man använder lösare i Excel med exempel
- hur man beräknar sammansatt intresse i Excel
- hur man beräknar CAGR (sammansatt årlig tillväxttakt) i Excel
Leave a Reply