grafen för en linjär ojämlikhet i en variabel är en tallinje. Använd en öppen cirkel för< och> och en sluten cirkel för kub och kub.

grafen för x> -3

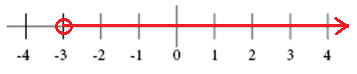
grafen för x 2

ojämlikheter som har samma lösning kallas ekvivalent. Det finns egenskaper av ojämlikheter liksom det fanns egenskaper av jämlikhet. Alla egenskaper nedan är också sanna för ojämlikheter som involverar bisexuell och bisexuell.

additionsegenskapen för ojämlikhet säger att lägga till samma nummer på varje sida av ojämlikheten ger en motsvarande ojämlikhet

$$If \: x>y,\: sedan\: x+z>y+z$$

$$If\: x<y,\: sedan\: x + z < y+z$$

subtraktionsegenskapen för ojämlikhet berättar att subtraktion av samma nummer från båda sidor av en ojämlikhet ger en likvärdig ojämlikhet.

$ $ If \: x>y,\: sedan\: x-z>y-z$

$$If\: x<y,\: sedan\: x-z<y-z$$

multiplikationsegenskapen för ojämlikhet berättar att multiplikation på båda sidor av en ojämlikhet med ett positivt tal ger en likvärdig ojämlikhet.

$ $ If \: x >y \: och\: z>0,\: sedan\: xz>yz$$

$$If\: x<y\: och\: z>0,\: sedan\: XZ<YZ$$

multiplikation på varje sida av en ojämlikhet med ett negativt tal å andra sidan ger inte en likvärdig ojämlikhet om vi inte också vänder riktningen för Ojämlikhetssymbolen

$$If \: X>y \: och\: Z<0,\: sedan\: XZ<YZ$$

$$om\: X<Y\: och\: z<0,\: sedan\: xz> yz$$

detsamma gäller för indelningsegenskapen för ojämlikhet.

uppdelning av båda sidor av en ojämlikhet med ett positivt tal ger en likvärdig ojämlikhet.

$$If \: x>y \: och\: z>0,\: sedan\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x<Y\: och\: z>0,\: sedan\: \ frac{x}{z} <\frac{y}{z}$$

och uppdelning på båda sidor av en ojämlikhet med ett negativt tal ger en likvärdig ojämlikhet om ojämlikhetssymbolen vänds.

$$If \: x>y \: och\: z<0,\: sedan\: \frac{x}{z}<\frac{y}{z}$$

$$If\: x<Y\: och\: z<0,\: sedan\: \frac{x}{z}>\frac{y}{z}$$

för att lösa en ojämlikhet i flera steg gör du som du gjorde när du löste ekvationer i flera steg. Ta en sak vid den tiden, helst börja med att isolera variabeln från konstanterna. När man löser ojämlikheter i flera steg är det viktigt att inte glömma att vända ojämlikhetstecknet när man multiplicerar eller delar med negativa tal.

exempel

Lös ojämlikheten

$$-2 \ vänster (x + 3 \ höger )< 10$$