av Jason McCormick
docent, Civil & miljöteknik, University of Michigan, Ann Arbor, MI, USA

Momentanslutningar gjorda av rektangulära och fyrkantiga ihåliga strukturella sektioner (HSS) har fått mindre hänsyn jämfört med HSS-till-HSS-anslutningar som består av axiellt laddade medlemmar (T -, Y -, cross-och K-anslutningar). Majoriteten av statiska studier med fokus på dessa anslutningar har övervägt Vierendeel trussystem. Dessa system bildas ofta av kvadratiska eller rektangulära övre och nedre ackord som är förbundna med kvadratiska eller rektangulära vertikala banelement (gren) (Figur 1). Som ett resultat av denna konfiguration genomgår ackord-till-webb-anslutningen betydande böjning tillsammans med skjuvning och axiella belastningar och anses inte vara en nålad anslutning som vanligtvis görs i typiska trussystem. Ursprungligen tänkt 1896 av Arthur Vierendeel, det var inte förrän HSS utvecklades att potentialen för Vierendeel fackverk började realiseras (Korol et al. 1977), men deras användning krävde en förståelse för hur man överför ögonblick mellan HSS-till-HSS T-anslutningar.

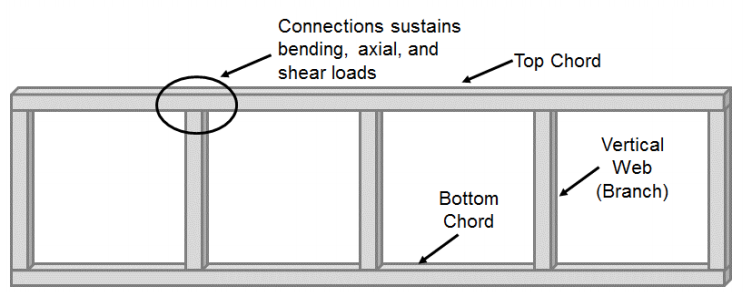
många av de tidiga studierna av dessa anslutningar fokuserade på anslutningens förmåga att utveckla grenmedlemmens fulla momentkapacitet. Jubb och Redwood (1966) visade att när grensektionen hade en lika bred bredd som ackordsektionen (kub=1) kunde HSS-medlemmens fulla momentkapacitet uppnås utan förstärkning. Denna studie ansåg emellertid inte den potentiella förlusten av momentkapacitet på grund av närvaron av axiell belastning. Å andra sidan, Korol et al. (1977) visade att anslutningar med en mindre grenbredd än ackordet inte kunde utveckla grenens fulla momentkapacitet utan att förstärka genom en serie av 29 olika anslutningstester med tanke på 5 olika konfigurationer (oförstörda, grenflänsförstärkande plattor, ackordflänsstyvningar, haunch och stympad pyramid). I allmänhet minskar styrkan och styvheten hos oförstörda anslutningar av Vierendeel-typ med en ökning av ackordsmalhetsförhållande (B/t) och minskning av gren-till-ackordbreddförhållande (kub). Som ett resultat kan ostifferade anslutningar av vierendeel-truss endast betraktas som styva (dvs. genomgå minimal relativ rotation mellan ackordet och grenen) när gren-till-ackordbreddförhållandet är 1,0 och ackordets slankhet är lågt eller anslutningen förstärks (Packer 1993).

eftersom de maximala ögonblicken i dessa fogar kan uppstå vid alltför stora deformationer, antas en liknande inställning till den som används för axiellt laddade kvadratiska och rektangulära HSS-fogar, där med en ultimat bärkraft eller en deformations-eller rotationsgräns används för att karakterisera designmomentet (Wardenier 1982). AISC 360-10 (Kapitel K3) beaktar tre gränstillstånd för kvadratiska och rektangulära HSS T-anslutningar under statisk böjning i planet: ackordväggplastifiering, sidovägg lokal avkastning och lokal avkastning av grenen på grund av Ojämn lastfördelning. Ackordväggplastifiering sker som ett resultat av att grendelens bredd är mindre än ackordets bredd (0,85) som kräver att spännings-och kompressionsbelastningar som produceras av böjmomentet överförs genom ackordets relativt flexibla yta snarare än direkt till de styvare sidoväggarna. Gränstillståndsekvationen (AISC 360-10 ekvation K3-6) kan härledas från avkastningslinjeteori (Figur 2):

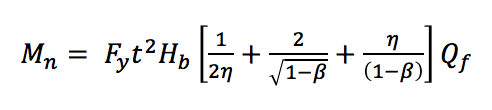
Mn är den nominella momentkapaciteten för anslutningen, Fy är den angivna minsta avkastningsstyrkan för ackordet, Hb är grenens totala höjd, h är lastlängdsparametern lika med grenens höjd dividerad med ackordets bredd (antar en 90o vinkel mellan ackordet och grenelementet som är typiskt för Vierendeel-fackverk), och QF är en parameter för att minska fogens kapacitet i närvaro av axiell kompression i ackordet.

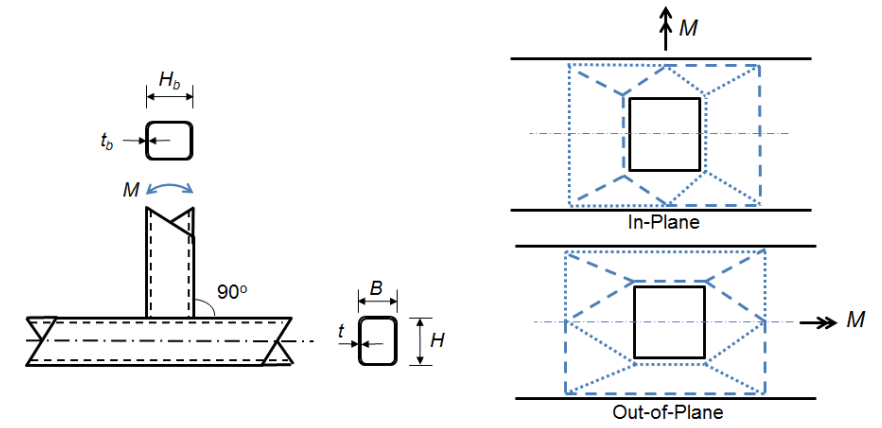
de andra två gränsstaterna är associerade med anslutningar där grendelens bredd är lika med eller nästan lika med ackordets bredd (kub> 0.85) vilket innebär att spännings-och kompressionsbelastningar som utvecklats i grendelens flänsar överförs nästan direkt till ackordets styvare sidoväggar. Gränstillståndet för sidovägg lokal avkastning (AISC 360-10 ekvation K3-7) för en T-anslutning kan sedan härledas från banan lokal avkastningsekvation för koncentrerade krafter applicerade på ett avstånd från änden av elementet större än dess djup (AISC 360-10 ekvation J10-2):

Mn = 0.5fyt(Hb + 5t)2
ekvation 2

för lokal avkastning av grenen på grund av ojämn belastningsfördelning (AISC 360-10 ekvation K3-8) i en T-anslutning används en effektiv breddsmetod för att minska kapaciteten hos stagelementet för att erhålla det nominella momentet som appliceras av staget:

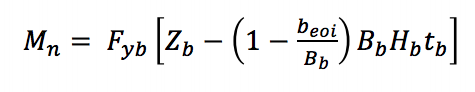
Fyb är den angivna minsta avkastningsstyrkan hos grenen, Zb är grenens plastsektionsmodul runt böjningsaxeln, beoi är grenens effektiva bredd, Bb är grenens totala bredd och tb är grenens väggtjocklek.

eftersom det finns begränsade experimentella bevis för att stödja specifika designmodeller för vierendeel fackverksanslutningar (t-anslutningar) under böjning utanför planet används analoga gränstillstånd som de för böjning i planet (Packer et al. 2010). Ett ytterligare gränstillstånd för ackorddistortionsfel utvecklas från vridmomentet som appliceras på ackordet av grenelementet som ett resultat av det Out-of-plane-ögonblicket. Detta vridmoment kan leda till rhomboidal förvrängning av ackordet. De nominella momentekvationerna för böjning utanför planet finns i AISC 360-10 ekvationer K3-9, K3-10, K3-11 och K3-12. Ekvationerna för både in-plane och Out-of-plane böjning av T-anslutningar liknar dem som har antagits internationellt (Packer et al. 2010).

ovanstående designekvationer härleddes med tanke på Vierendeel trussystem under statiska belastningar. En ny studie (Fadden et al. 2015) har främjat detta arbete för att överväga beteendet hos kvadratiska och rektangulära HSS-till-HSS-momentanslutningar under stora cykliska belastningar för användning i rörbaserade seismiska momentramsystem (mellanliggande och speciella momentramar). Ett sådant system ser ut att dra nytta av de utmärkta axiella, böjnings-och vridningsegenskaperna, förhållandet mellan hög hållfasthet och vikt och arkitektoniskt tilltalande karaktär av kvadratisk och rektangulär HSS. Det höga vridmotståndet kan leda till en minskning av strålens laterala stag medan det höga hållfasthets-till-viktförhållandet resulterar i lägre seismisk massa. Sådana anslutningar måste emellertid kunna genomgå stabil plasthingning av strålelementet där 80% av strålelementets plastkapacitet bibehålls till antingen 0,2 rad. (IMF) eller 0,4 rad. (SMF) av Inter-story drift (AISC 341-10). Med tanke på att den nuvarande seismiska utformningen av momentramsystem kräver att majoriteten av det oelastiska beteendet uppträder i strålelementet, måste strålelementet också nå sin fulla plastkapacitet innan de genomgår lokal buckling. Fadden och McCormick (2014a) ansåg både experimentella och finita elementmodeller för att bestämma begränsande breddtjocklek och djuptjocklekskrav för HSS under böjning eftersom de som anges i de nuvarande AISC seismiska bestämmelserna (AISC 341-10) utvecklades till stor del baserat på tester av cykliska axiellt laddade HSS-medlemmar.

för att bestämma lämpliga konfigurations-och detaljkrav för att möta detta krav på styrka och duktilitet testades fyra olika anslutningskonfigurationer experimentellt: två direktsvetsade icke förstärkta anslutningar (oöverträffade och matchade) och två förstärkta anslutningar (genom platta och extern membranplatta). Alla anslutningar använde en HSS 10x10x5 / 8 kolumn. De direktsvetsade anslutningarna använde förkvalificerade CJP-svetsar enligt AWS D1.1 (2010). För den oöverträffade anslutningen var strålen en HSS 12x8x3 / 8 (ml = 0.8) att föreslå att plastifiering av kolonnytan kan vara ett problem. För den matchade anslutningen var strålen en HSS 12x10x3 / 8 (KB = 1.0) som gjorde att lasterna kunde överföras direkt till sidoväggen. AISC-laddningsprotokollet för förkvalificering av seismiska momentanslutningar användes (AISC 341-10) för att ladda anslutningarna. Anslutningsbeteendet var som förväntat med den oöverträffade anslutningen som visade deformation vid kolonnytan, medan den matchade anslutningen kunde överföra lasten till kolonnens sidoväggar. Båda anslutningarna misslyckades emellertid på grund av brott i kolonnens basmetall vid tån på svetsens hörn (Figur 3). Detta spröda misslyckande vid rotationer på 0,4 rad. och 0,5 rad. bekräftade att direktsvetsade anslutningar inte ger lämpligt beteende för seismiska applikationer.

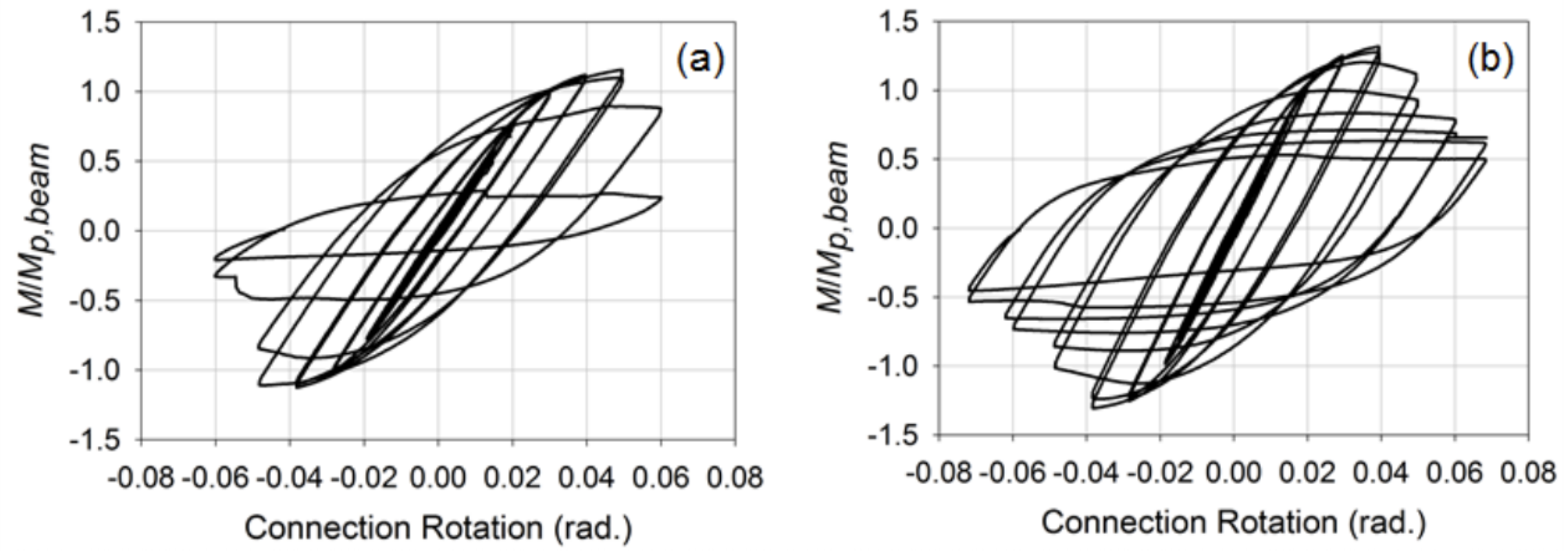
de förstärkta anslutningarna utvecklades sedan med tanke på genom platta och externa membranplattor som ofta används i bred fläns Balk-till-HSS kolonnanslutningar för att ge en bättre mekanism för att överföra spännings-och kompressionskrafterna till kolonnens sidovägg och minimera spänningskoncentrationer placerade på svetsarna. För dessa anslutningar var strålarna HSS 12x8x3 / 8 (KB = 0,8) medlemmar. Information om det specifika förfarande som används för att utforma och detaljera dessa anslutningar finns i Fadden och McCormick (2014b) och Fadden et al. (2015). Placerad under samma belastning som de oförstörda anslutningarna visade anslutningarna ett mer stabilt beteende med plastgångjärnet som inträffade bort från kolonnytan vid änden av den genomgående eller yttre membranplattan (Figur 4). Båda anslutningarna kunde också nå 0,4 rad. att genomgå lokal buckling vilket resulterade i nedbrytning av momentkapaciteten. Fraktur initierade emellertid i hörnet av HSS-strålen på grund av cykling vid stora rotationsnivåer på 0,7 rad. En jämförelse av de normaliserade momentrotationskurvorna för de matchade och externa membranplattanslutningarna kan ses i Figur 5. Sammantaget visade de förstärkta anslutningarna löfte om användning av HSS-till-HSS seismiska momentramsystem, men mer arbete är nödvändigt för att flytta dessa anslutningar mot eventuell förkvalifikation.

AISC. (2010). ”Seismiska bestämmelser för strukturella stålbyggnader”. ANSI / AISC 341-10. Amerikanska institutet för stålkonstruktion, Chicago, IL.

AISC. (2010). ”Specifikationer för strukturella stålbyggnader”. ANSI / AISC 360-10. Amerikanska institutet för stålkonstruktion, Chicago, IL.

AWS. (2010). ”Strukturell Svetskod”. ANSI / AWS D1. 1, American Welding Society, Miami, FL.

Fadden, F. och McCormick, J. (2014a). ”Finit Elementmodell av det cykliska Böjningsbeteendet hos ihåliga strukturella sektioner”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. och McCormick, J. (2014b). ”HSS-till-HSS seismisk Momentanslutning prestanda och Design”. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D. och McCormick, J. (2015). ”Cyklisk testning av svetsade HSS-till-HSS-Momentanslutningar för seismiska applikationer”. ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J. E. M. och Redwood, R. G. (1966). ”Design av fogar till Lådsektioner”. Institutionen för byggnadsingenjörer, konferens om Industrialiserad byggnad och byggnadsingenjör, Institute of Structural Engineers, London.

Korol, R. M., El-Zanaty, M. och Brady, F. J. (1977). ”Ojämn bredd anslutningar av fyrkantiga ihåliga sektioner i Vierendeel fackverk”. Kanadensisk tidskrift för civilingenjör, 4, 190-201.

Packer, J. A. (1993). ”Momentförbindelser mellan rektangulära ihåliga sektioner”. Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. och Kurobane, Y. (2010). Design Guide 3: för rektangulära ihåliga avsnitt (RHS) fogar under övervägande statisk belastning 2: a upplagan. CIDECT, Kanada.

Wardenier, J. (1982). ”Ihåliga Sektionsfogar”. Delft University Press, Delft, Nederländerna.

September 2016

ladda ner PDF