komplexa tal: introduktion (sidan 1 av 3)

avsnitt: introduktion, operationer med komplex, den kvadratiska formeln

hittills har du fått veta att du inte kan ta kvadratroten av ett negativt tal. Det beror på att du inte hade några siffror som var negativa efter att du hade kvadrerat dem (så att du inte kunde ”gå bakåt” genom att ta kvadratroten). Varje nummer var positivt efter att du kvadrerade det. Så du kunde inte mycket väl kvadratrota en negativ och förvänta dig att komma med något förnuftigt.

Nu kan du dock ta kvadratroten av ett negativt tal, men det innebär att du använder ett nytt nummer för att göra det. Detta nya nummer uppfanns (upptäcktes?) runt tiden för reformationen. Vid den tiden trodde ingen att någon ”verklig värld” – användning skulle hittas för detta nya nummer, förutom att lätta på beräkningarna som är involverade i att lösa vissa ekvationer, så det nya numret betraktades som ett låtsas nummer som uppfanns för enkelhets skull.

( men då, när du tänker på det, är inte alla siffror uppfinningar? Det är inte som siffror växer på träd! De lever i våra huvuden. Vi gjorde dem alla upp! Varför inte uppfinna en ny, så länge det fungerar okej med det vi redan har?)

annons

sedan:

nu kanske du tror att du kan göra det här:

men det gör ingen mening! Du har redan två nummer som kvadrerar till 1; nämligen -1 och +1. Och jag kvadrerar redan till -1. Så det är inte rimligt att jag också skulle kvadrera till 1. Detta pekar på en viktig detalj: När du arbetar med imaginaries får du något (förmågan att hantera negativ inuti kvadratrötter), men du förlorar också något (en del av den flexibilitet och praktiska regler du brukade ha när du handlade med kvadratrötter). I synnerhet måste du alltid göra i-delen först!

• förenkla sqrt(-9). Copyright amazing Elizabeth Stapel 2000-2011 All Rights Reserved

(Varning: steget som går igenom det tredje” lika ”tecknet är””, inte””. Jag är utanför den radikala.)

• förenkla sqrt(-25).

• förenkla sqrt(-18).

• förenkla –sqrt(-6).

i dina beräkningar kommer du att hantera jag precis som du skulle göra med x, förutom att x2 bara är x2, men i2 är -1:

• förenkla 2i + 3i.

2i + 3i = (2 + 3)i = 5I

• förenkla 16I – 5I.

16i – 5i = (16 – 5)i = 11i

• multiplicera och förenkla (3i)(4i).

(3i) (4i) = (3 * 4) (i·i) = (12) (i2) = (12)(-1) = -12

• multiplicera och förenkla (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(I2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

notera detta sista problem. Inom det kan du se att , eftersom I2 = -1. Fortsätter vi får:

detta mönster av krafter, tecken, 1 och i är en cykel:

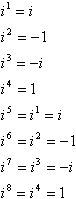
med andra ord, för att beräkna någon hög effekt av i, kan du konvertera den till en lägre effekt med hjälp av att ta närmaste multipel av 4 som inte är större än exponenten och subtrahera denna multipel från exponenten. Till exempel är en vanlig trickfråga på tester något i linje med ”förenkla i99”, tanken är att du ska försöka multiplicera jag nittionio gånger och du får slut på tid, och lärarna kommer att få en bra fniss på din bekostnad i fakultetsloungen. Så här fungerar genvägen:

i99 = i96+3 = i(4 24 24)+3 = i3 = –i

det vill säga, i99 = i3, eftersom du bara kan lop off i96. (Nittiosex är en multipel av fyra, så i96 är bara 1, som du kan ignorera.) Med andra ord kan du dela exponenten med 4 (med lång division), kassera svaret och bara använda resten. Detta ger dig den del av exponenten som du bryr dig om. Här är några fler exempel:

• förenkla I17.

i17 = i16 + 1 = i4 · 4 + 1 = I1 = I

• förenkla I120.

i120 = i4 · 30 = i4· 30 + 0 = I0= 1

• förenkla I64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>