kommer ett gammalt problem att ge en ny insikt? Kanske ett elegant bevis på 4-färgs teorem?
4-färgproblemet är ett av de mest kända matematiska problemen. Det motstod bevis i mer än hundra år innan det slutligen gav efter; i slutändan fanns det ett giltigt bevis, men ett som förlitade sig på mer än tusen timmars datortid. Jim Tilleys forskning tyder på att en dramatisk förenkling i slutändan kan vara möjlig. Han har upptäckt en egenskap, Kempe-locking, att ett minsta motexempel till 4-färgsatsen måste uppvisa och har formulerat en gissning, baserad på omfattande undersökningar, att Birkhoff-diamanten är den enda grundläggande Kempe-låskonfigurationen.
Graffärgning innebär att tilldela etiketter eller färger till hörn av ett matematiskt objekt som kallas en graf. 4-färgproblemet gav en av de ursprungliga motivationerna för utvecklingen av algebraisk grafteori. Graffärgning används i många verkliga problem, som att minimera konflikter vid schemaläggning av sportevenemang, planering av provscheman och organisering av sittplaner, även för CCTV-kameraplacering i en byggnad med många hörn för att minimera överlappningen av kameran. Det ger också grunden för Sudoku pussel.
4-färgproblemet
Francis Guthrie, en student av den berömda brittiska matematikern och logikern Augustus De Morgan, ställde 4-färgproblemet 1852. Han formulerade problemet med avseende på kartor som uppfyller vissa villkor, som att inte innehålla några hål och ha varje region (t.ex. land eller stat) ansluten så att ingen region finns i två eller flera icke-angränsande delar. Guthrie hävdade att för sådana kartor skulle det aldrig ta mer än fyra färger för att färga kartan så att inga två grannregioner var samma färg.
numera uttrycks 4-färgproblemet i termer av grafer, och i stället för färgregioner i kartor, En färger hörn i grafer. Alla befintliga bevis på 4-färgs teorem visar att ett minsta motexempel inte kan existera. (Ett minsta motexempel är den minsta plana grafen som kräver mer än fyra färger för en korrekt färgning av dess hörn.) Endast plana grafer som är trianguleringar måste beaktas, eftersom alla grafer som inte är en triangulering kan omvandlas till en genom att infoga kanter. Om den resulterande trianguleringen är 4-färgad, är den ursprungliga grafen också 4-färgad. Det är mycket användbart att kunna begränsa sin granskning till trianguleringar.

ett tidigt försök till bevis
av dem som erbjöd ett bevis, Alfred Bray Kempe, en engelsk barrister och amatörmatematiker, var den person vars rykte var mest besvärad av hans misslyckade ansträngning. Han tillkännagav sin framgång 1879 och hans’ bevis ’ publicerades i American Journal of Mathematics. Elva år senare skapade emellertid en annan engelsk matematiker, Percy Heawood, en karta som han 4-färgade upp till den slutliga regionen på ett sådant sätt att Kempes metod misslyckades för den slutliga regionen. Trots hans misslyckande lämnade Kempe ett användbart verktyg-en Kempe-kedja. Det är en maximal, ansluten (varje toppunkt som kan nås från någon annan genom en väg längs kanterna) undergraf där alla hörn använder exakt två färger. Kempe-kedjor har visat sig vara avgörande för färg-och omfärgningsgrafer. Se Figur 1.
det skulle vara en häpnadsväckande förenkling
om Birkhoff-diamanten ensam är nyckeln till 4-färgbarhet.
äntligen
det första giltiga beviset tillkännagavs 1976 av Kenneth Appel och Wolfgang Haken. Det krävde över tusen timmars datortid för att verifiera särskilda aspekter av deras argument. Denna uppfattning att förlita sig på datorkod, potentiellt innehållande mänskliga inducerade fel (och deras kod gjorde!), snarare än ett ’mänskligt’ bevis, har inte uppfyllt en stor del av det matematiska samfundet. Appel och hakens bevis var elegant i sin övergripande struktur, men detaljerna var fula. beviset förfinades 1996 av ett team av fyra matematiker: Robertson, Sanders, Seymour och Thomas, men de förlitade sig fortfarande på datorkod för att slutföra sitt bevis. Under 2010 erbjöd Steinberger en annan variation. Det finns dock fortfarande inget helt tillfredsställande svar på varför 4-färgssatsen är sant. (När gissningen bevisades fick den status som en sats.’)

sökandet efter ett alternativt bevis
4-färgproblemet är så lätt att formulera och förstå att det har väckt intresse för tusentals amatörmatematiker, alla tror att de kan hitta ett enkelt klassiskt bevis och därmed bli kända. Jim Tilleys far, fysiker och rektor för Kanadas Royal Military College från 1978-1984, var en sådan drömmare. När han kände att han hade gjort ett genombrott, skulle han be sin son, Jim, att kontrollera sitt arbete. Jim hittade alltid en brist. Trots sin första skepsis att hans fars ansträngningar någonsin skulle bära frukt, blev han smittad med en entusiasm för 4-färgproblemet och började studera det intensivt.
Kempe-locking
Jim Tilleys forskning ledde till att han upptäckte en ny egenskap som ett minsta motexempel på 4-färgs teorem måste uppvisa. Han kallade det ’ Kempe-locking.- Han insåg att det sannolikt skulle vara oförenligt med en annan egenskap som ett minsta motexempel måste uppvisa – dvs., hur ansluten en graf är (hur många hörn måste tas bort från en graf innan den faller isär).
Tilleys Kempe-låsning är en egenskap associerad med en kant i en triangulering. Begreppet börjar med att ta bort en kant xy mellan intilliggande hörn x och y. Om för varje 4-färgning av den resulterande grafen där färgerna på x och y är desamma, finns det ingen sekvens av färgutbyten på Kempe-kedjor som får färgen på x att skilja sig från färgen på y, sägs den ursprungliga trianguleringen vara Kempe-låst med avseende på kanten xy. Tilley bevisade att ett minsta motexempel till 4-färgs sats måste Kempe-låst med avseende på var och en av dess kanter; varje kant i ett minimum motexempel måste ha denna färg egendom.
Kempe-låsning är ett särskilt restriktivt tillstånd som blir svårare att tillfredsställa när en triangulering blir större. Tilley bestämde sig för att upptäcka om det finns något gemensamt för trianguleringar som har Kempe-låsta kanter. Hans tidigaste sökning efter Kempe-låsning ledde honom till Birkhoff diamond.

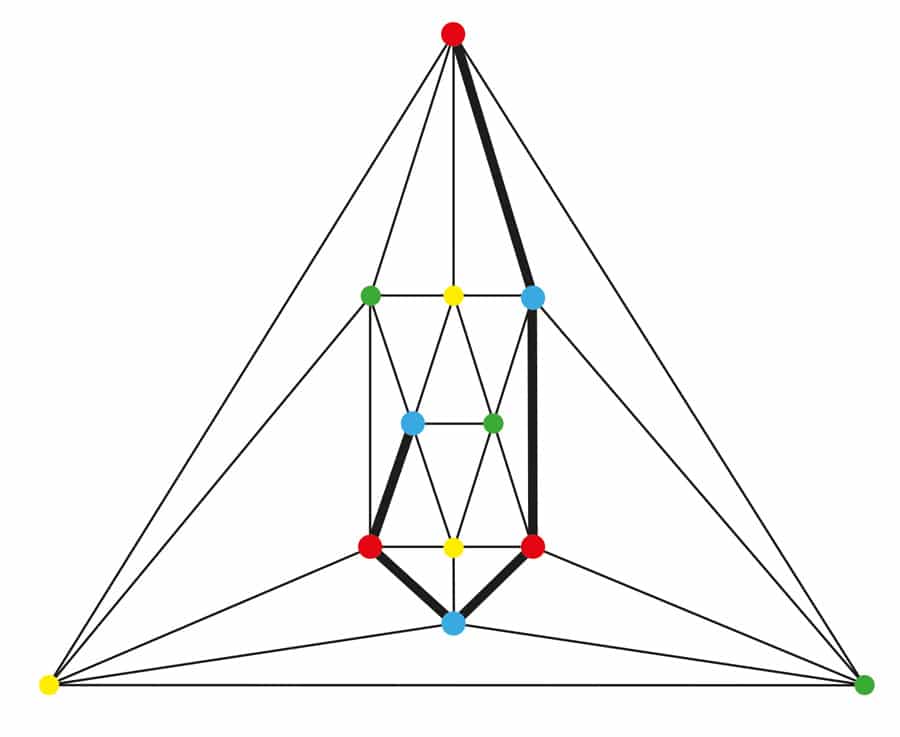
Figur 3. Två plana grafer, en en 4-ansluten triangulering på 6 hörn och en en 5-ansluten triangulering på 17 hörn.
Birkhoff diamond
1913 upptäckte GD Birkhoff att en viss konfiguration av tio länder i en karta (en gränsring av sex länder som omsluter en uppsättning av fyra länder) har en viktig egenskap. Om den konfigurationen finns på en karta och om underkartan med den borttagna konfigurationen är 4-färgad, blir hela kartan 4-färgad. Således kan ett minsta motexempel inte innehålla den specifika konfigurationen. Det har blivit känt som Birkhoff diamond. Tilley fann att en Kempe-låst kant xy verkar uppstå endast när x och y också är slutpunkterna i grafversionen av en Birkhoff-diamant. Se Figur 2.
gissningen är lätt uttryckt, förståelig och spännande och erbjuder en övertygande förklaring till varför alla plana grafer är 4-färgade.
att inte ha stött på någon Kempe-låskonfiguration utan en Birkhoff-diamant, antog han att Birkhoff-diamanten är den enda ’grundläggande’ Kempe-låskonfigurationen, en som inte innehåller en mindre Kempe-låskonfiguration som en undergraf. Tilley fann dock att han inte kunde bevisa sin kritiska gissning. Det var frustrerande eftersom, om sant, gissningar skulle direkt bevisa 4-färg sats. (För att vara ett minsta motexempel skulle en triangulering behöva innehålla en Birkhoff diamond subgraph, men om det gjorde det kunde det inte vara ett minsta motexempel.)
ett överväldigande stödfall
istället för att bevisa sin gissning gjorde Tilley det näst bästa. Han bestämde sig för att spela rollen som en experimentalist och bygga ett överväldigande fall för att stödja hans gissning. Han delade alla relevanta plana trianguleringar i två klasser: de där minst fyra hörn måste tas bort innan graferna faller isär (4-anslutna) och de där minst fem hörn måste tas bort innan graferna faller isär (5-anslutna). Se Figur 3. Hjälpsam i Tilleys omfattande sökning var att han bara var tvungen att undersöka en medlem av varje isomorfismklass (grafer som är strukturellt identiska). Tilley undersökte alla 8 044 isomorfismklasser av 4-anslutna plana trianguleringar på upp till 15 hörn och alla 9 733 isomorfismklasser av 5-anslutna plana trianguleringar på upp till 24 hörn. Han hittade bara tre Kempe-låsta trianguleringar. Varje upptäckt Kempe-låst kant innehöll en Birkhoff-diamant och var och en inträffade i en 4-ansluten triangulering. Det fanns ingen alls bland 5-anslutna trianguleringar.

Tilley utvidgade sin sökning bland 4-anslutna trianguleringar genom att undersöka alla 30 926 isomorfismklasser på 16 hörn och alla 158 428 isomorfismklasser på 17 hörn. Beräkningstidsbegränsningar innebar att han begränsade sin sökning till prover av 100 000 slumpmässigt genererade icke-isomorfa trianguleringar vardera för klasser på 18,19 Och 20 hörn. Den utökade sökningen dök upp 45 ytterligare Kempe-låsta trianguleringar, men exakt samma resultat som den ursprungliga sökningen: varje Kempe-låst kant i en triangulering innehöll en tillhörande Birkhoff diamant.
var härifrån?
Tilleys omfattande sökningar bekräftade lätt att Birkhoff diamond är en grundläggande Kempe-låskonfiguration. Han har noggrant testat sin gissning, men det är fortfarande obevisat. Om (eller när) Tilleys gissning bevisas sant, dvs att Birkhoff-diamanten ensam är nyckeln till 4 – färgbarhet, skulle det vara en häpnadsväckande förenkling av problemet: en enda konfiguration som förklarar allt-matematisk elegans.

att bevisa 4-färgens gissning krävde många framstående matematikers ansträngningar. Tilleys gissning att Birkhoff diamond är den enda grundläggande Kempe-låskonfigurationen kan vara ännu svårare att bevisa. De experimentella bevisen är dock starka. Teoretiker kan säga ’ varför bry sig?”Tilleys svar är att omättlig nyfikenhet kommer att vinna ut:” när allt kommer omkring är gissningen lätt uttryckt, förståelig och spännande och erbjuder en övertygande förklaring till varför alla plana grafer är 4-färgade.”
personligt svar
vad ledde ursprungligen din entusiasm för 4-färgproblemet och ledde dig att studera det så intensivt?
det var min fars besatthet av problemet i sin pension och hans önskan att använda mig som bollplank för sina tankar.
vad är dina planer för framtida forskning inom detta område?
Jag har nyligen granskat ett komplicerat papper som involverar en helt annan inställning till 4-färgproblemet. Som papperet står, tror jag att det har brister. Ändå har det löfte. Jag kan bli frestad att utforska ett samarbete.
Leave a Reply