purplemath

”interquartile range”, förkortat ”IQR”, är bara bredden på rutan i box-and-whisker-plottet. Det vill säga IQR = Q3 – Q1 . IQR kan användas som ett mått på hur utspridda värdena är.

statistik förutsätter att dina värden är grupperade kring något centralt värde. IQR berättar hur utspridda de” mellersta ” värdena är; det kan också användas för att berätta när några av de andra värdena är ”för långt” från det centrala värdet. Dessa” för långt borta ”punkter kallas ”outliers”, eftersom de” ligger utanför ” det område där vi förväntar oss dem.

IQR är längden på lådan i din box-and-whisker-plot. En outlier är något värde som ligger mer än en och en halv gånger längden på lådan från vardera änden av lådan.

innehållet fortsätter under

MathHelp.com

det vill säga, om en datapunkt är under Q1 – 1.5 c / IQR eller över Q3 + 1.5 c / IQR, anses den vara för långt från de centrala värdena för att vara rimlig. Kanske stötte du på vägskalan när du gjorde den enda mätningen, eller kanske din labbpartner är en idiot och du borde aldrig ha låtit honom röra vid någon av utrustningen. Vem vet? Men oavsett deras orsak är outliers de punkter som inte verkar ”passa”.

När du är bekväm att hitta IQR kan du gå vidare till att hitta outliers, om någon.

• hitta eventuella avvikelser för följande datamängd:

värdena för Q1 – 1.5 IQR och Q3 + 1.5. IQR är de ” staket ”som markerar de” rimliga ” värdena från outlier-värdena. Outliers ligger utanför staketet.

Om ditt uppdrag har du överväga inte bara extremvärden utan också ”extrema värden”, då värdena för Q1 – 1.5 IQR och Q3 + 1.5 IQR är de” inre ”staket och värdena för Q1 – 3 IQR och Q3 + 3 IQR är de” yttre ” staket.

avvikelserna (markerade med asterisker eller öppna prickar) ligger mellan de inre och yttre staketet, och de extrema värdena (markerade med vilken symbol du inte använde för avvikelserna) ligger utanför de yttre staketet.

förresten, din bok kan hänvisa till värdet av ” 1.5 kubiqr ”som ett”steg”. Då kommer avvikelserna att vara siffrorna som ligger mellan ett och två steg från gångjärnen, och extremt värde kommer att vara siffrorna som är mer än två steg från gångjärnen.

om man tittar igen på föregående exempel skulle de yttre staket vara på 14,4-3 8,5 0,5 = 12,9 och 14,9 + 3 0,5 0,5 = 16,4. Eftersom 16.4 är rätt på det övre yttre staketet, skulle detta anses vara bara en outlier, inte ett extremt värde. Men 10.2 är helt under det nedre yttre staketet, så 10.2 skulle vara ett extremt värde.

din grafkalkylator kanske inte anger om en box-and-whisker-plot innehåller avvikare. Till exempel innehåller ovanstående problem punkterna 10.2, 15.9 och 16.4 som outliers. En inställning på min grafräknare ger den enkla box-and-whisker-plottet som endast använder sammanfattningen med fem nummer, så de längsta avvikelserna visas som slutpunkterna för whiskers:

en annan calculator inställning ger box-and-whisker plot med outliers speciellt markerade (i detta fall, med en simulering av en öppen punkt), och whiskers går bara så långt som de högsta och lägsta värden som inte är outliers:

min kalkylator gör ingen skillnad mellan outliers och extrema värden. Din kanske inte heller. Kontrollera din bruksanvisning nu, innan nästa test.

Om du använder din grafräknare för att hjälpa till med dessa tomter, se till att du vet vilken inställning du ska använda och vad resultaten betyder, eller räknaren kan ge dig ett helt korrekt men ”fel” svar.

• hitta eventuella extremvärden för följande datauppsättning och rita box-and-whisker-plottet. Markera eventuella avvikare med en asterisk och eventuella extrema värden med en öppen punkt.

annons

för att hitta outliers och extrema värden måste jag först hitta IQR. Eftersom det finns sju värden i listan är medianen det fjärde värdet, så:

Q2 = 25

den första halvan av listan är:

21, 23, 24

…så Q1 = 23; den andra halvan är:

29, 33, 49

…så Q3 = 33. Sedan ges IQR av:

IQR = 33 – 23 = 10

avvikelserna kommer att vara några värden nedan:

23 – 1.5×10 = 23 – 15 = 8

…eller högre:

33 + 1.5×10 = 33 + 15 = 48

de extrema värdena kommer att vara de nedan:

23 – 3×10 = 23 – 30 = -7

…eller högre:

33 + 3×10 = 33 + 30 = 63

Så jag har en outlier vid 49 men inga extrema värden. Jag kommer inte ha en topp whisker på min tomt eftersom Q3 också är den högsta icke-outlieren. Så min tomt ser ut så här:

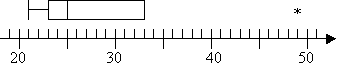
det bör noteras att de metoder, termer och regler som beskrivs ovan är vad jag har lärt och vad jag oftast har sett undervisat. Din kurs kan dock ha olika specifika regler, eller din kalkylator kan göra beräkningar något annorlunda. Du kan behöva vara lite flexibel för att hitta de svar som är specifika för din läroplan.